Learning 方法有什么致命缺点吗？我认为目前 Learning 方法还存在的较为棘手的问题是，有时候结果会出现非常低级的错误，或是说不可思议不合常理的 cornercases。所以我认为一个工程系统或是一个鲁棒的算法系统，在 Learning 之后做一个基于常理（如 geometry 约束或专家系统）的验证，能有效抑制这个问题。本文就是一个比较好的 learning+geometry 想结合的方法。
本文[1]基于图像语义及几何信息，通过 3D 目标的稀疏与密集约束，提出了一种准确的 3D 目标检测方法。根据输入数据的类型，作者将 3D 检测分为三大类：
- LiDAR-based，近期被研究的较多，基本是自动驾驶所必须的；
- Monocular-based，低成本方案；
- Stereo-based，相比 Monocular-based，有优势，但是研究较少；
本文就是 Stereo-based 3D 检测方案。不同于一般的 rgb+depth 作为输入的方案，本文直接将左右目 rgb 作为输入，没有显示地 depth 生成过程。工程上来说，这也极大地缩短了 3D Detection 的时延(latency)。
本文方法如图 1 所示，主要有三部分组成：
- Network，又有三部分构成：
- Stereo RPN Module，输出左右图的 RoI；
- Classification and Regression branches，输出目标类别，朝向，尺寸；
- Keypoint branch，输出左目目标的关键点；
- Sparse constraints，3D 框-2D 框的稀疏约束；
- Dense constraints，准确定位的关键模块；
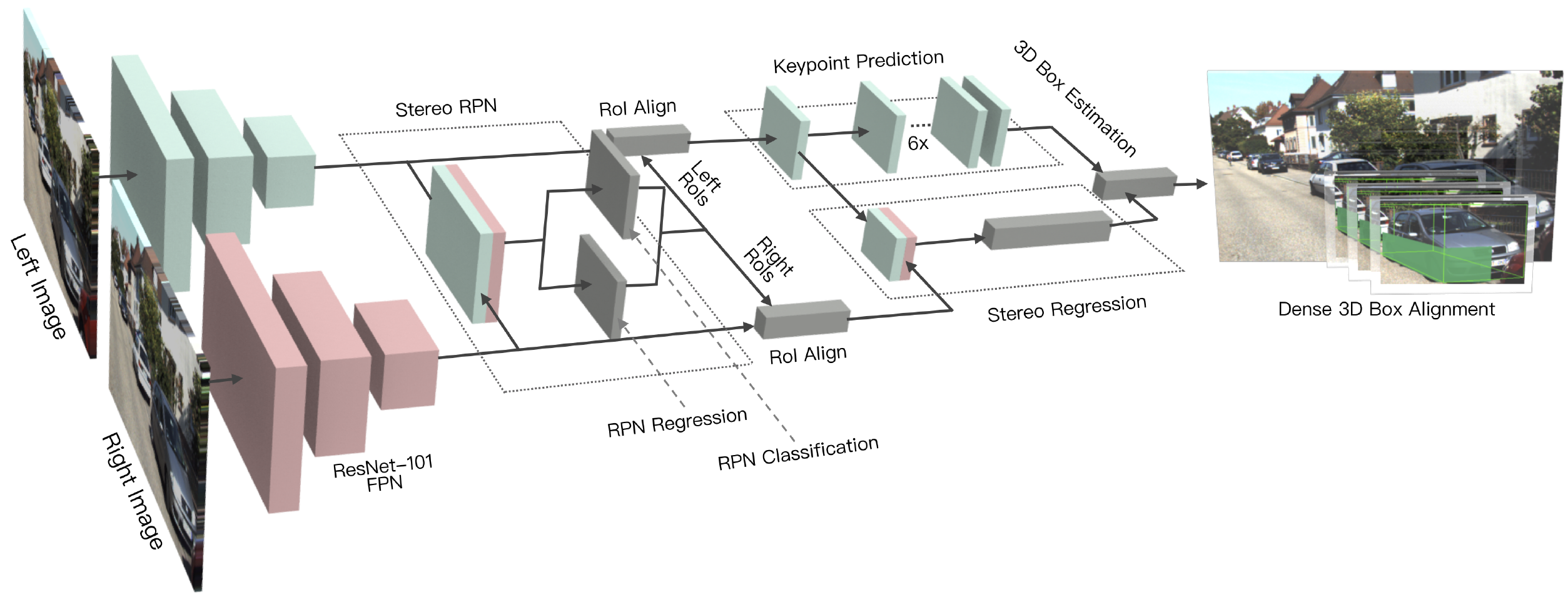
1. Stereo R-CNN Network
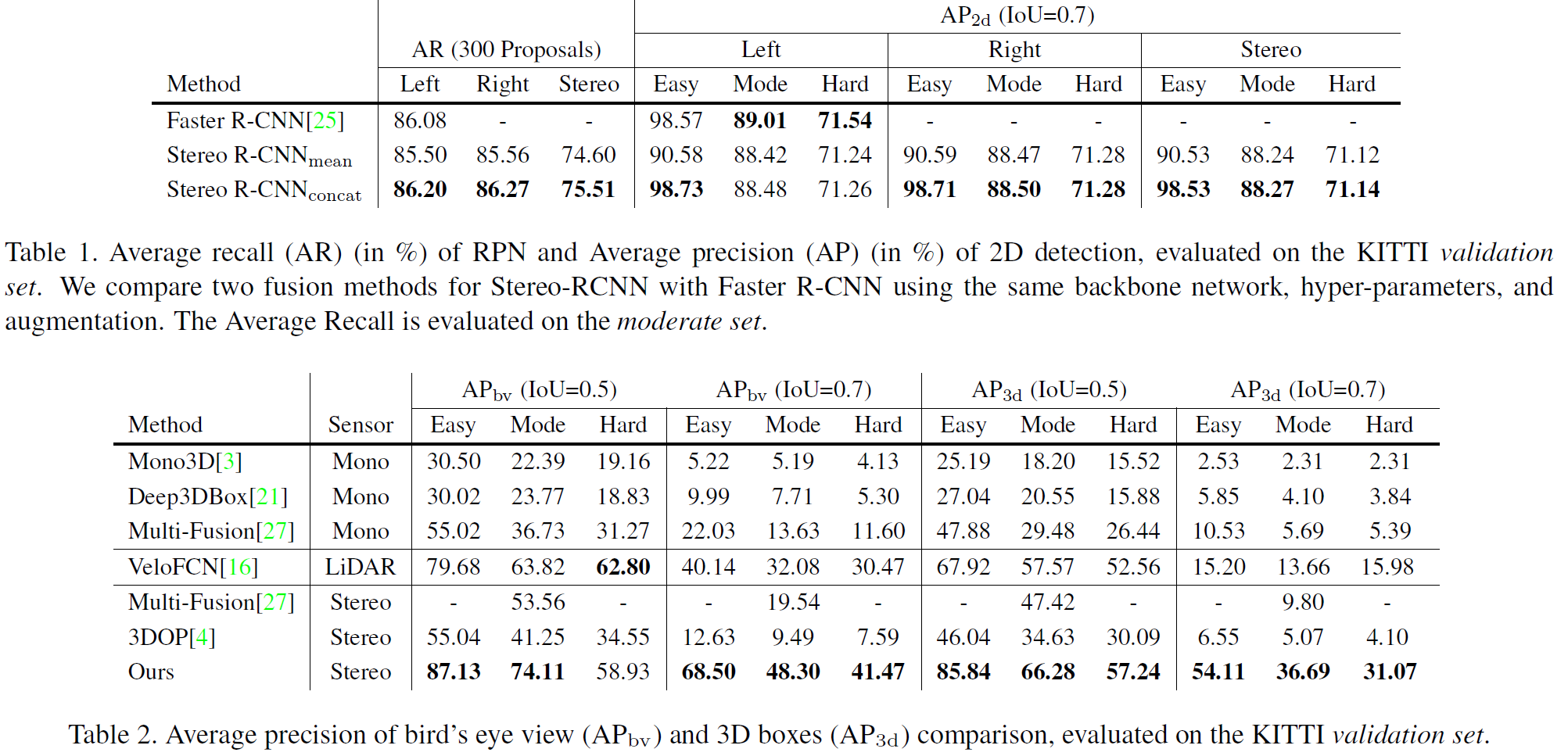
Stereo R-CNN 是在 Faster R-CNN 基础上，同时检测与关联左右目图像 2D 框的微小差异。
1.1. Stereo RPN
在传统 RPN 网络的基础上，本文先对左右图做 paramid features 提取，然后将不同尺度的特征 concatenate 一起，进入 RPN 网络。 
关键的一点是 objectness classification与 stereo box regression 的真值框定义不一样。如图 2 所示，
- 对于 objectness classification，真值框定义为左右目真值框的外接合并（union GT box），一个 anchor 在与真值框的交并比（Intersection-over-Union）大于 0.7 时标记为正样本，小于 0.3 时标记为负样本。分类任务的候选框包含了左右目真值框区域的信息。
- 对于 stereo box regression，真值框定义为左右目分别的真值框。待回归的参数定义为 \([u, w, u', w', v, h]\)，分别为左目的水平位置及宽，右目的水平位置及宽，垂直位置及高。因为输入为矫正过的左右目图像，所以可认为左右目的垂直方向上已经对齐。
每个左右目的 proposal 都是通过同一个 anchor 产生的，自然左右目的 proposal 是关联的。通过 NMS 后，保留左右目都还存在的 proposal 关联对，取前 2000 个用于训练，测试时取前 300 个。
1.2. Stereo R-CNN
网络头包含两大部分：
Stereo Regression
左右目的 proposal 关联对，分别在左右目的 feature 上进行 RoI Align 的操作，然后 concatenate 输入到全链接层。左右目的 RoI 对与真值框的 IoU 均大于 0.5 时定位正样本，左右目的 RoI 对与真值框的 IoU 有一个小于 0.5 且大于 0.1，则定位负样本。用四个分支分别预测：- object class；
- stereo bounding boxes，与 stereo rpn 中一致，左右目的高度已对齐；
- dimension，先统计平均的尺寸，然后预测相对量；
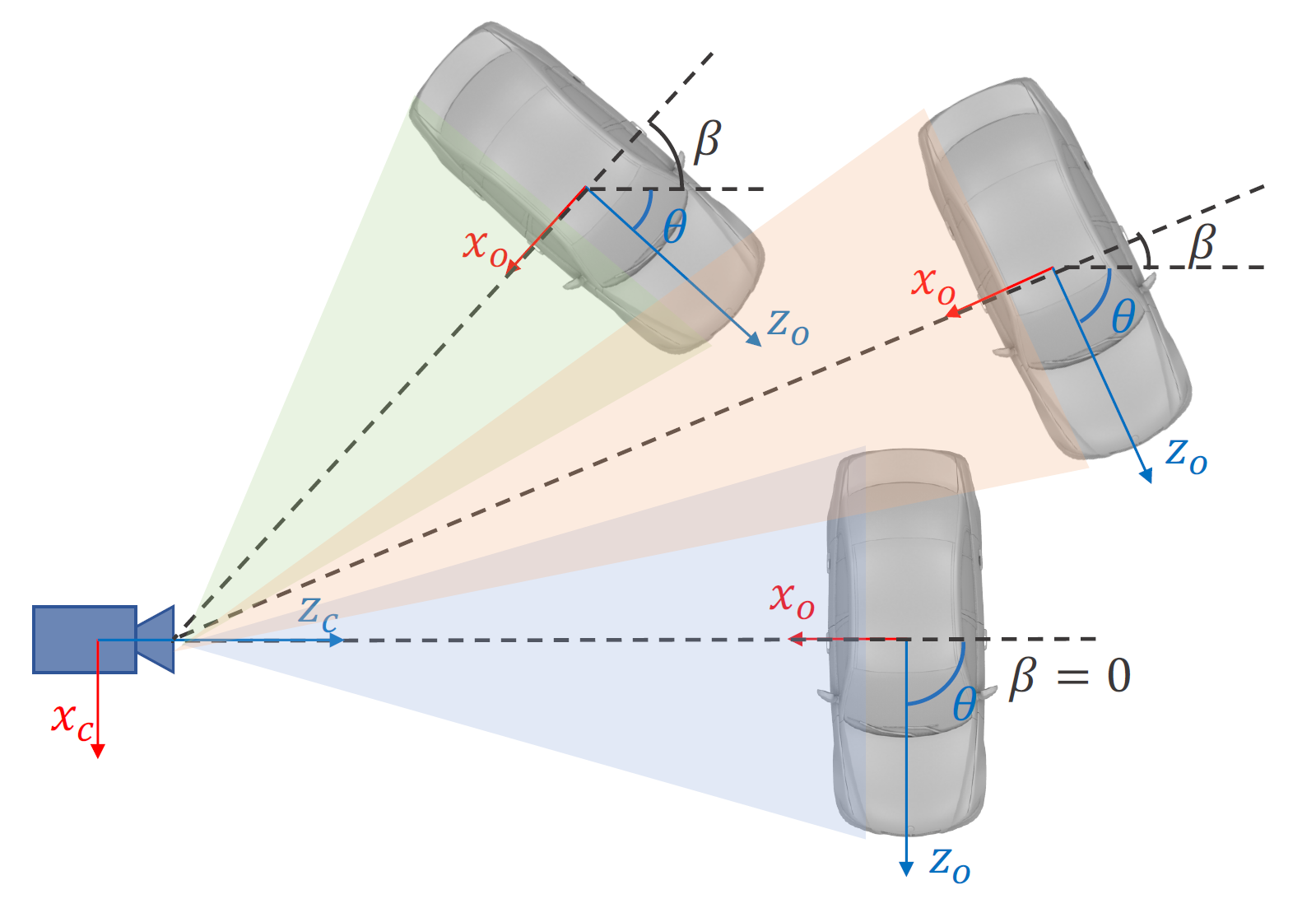
- viewpoint angle，如图 3 所示，\(\theta\) 为相机坐标系下的朝向角，\(\beta\) 为相机中心点下的方位角(azimuth)，这三个目标在相机视野下是一样的，所以我们回归的量是视野角(viewpoint angle) \(\alpha=\theta+\beta\)，其中 \(\beta=arctan\left(-\frac{x}{z} \right) \)。并且为了连续性，回归量为 \([sin\,\alpha,cos\,\alpha]\)。
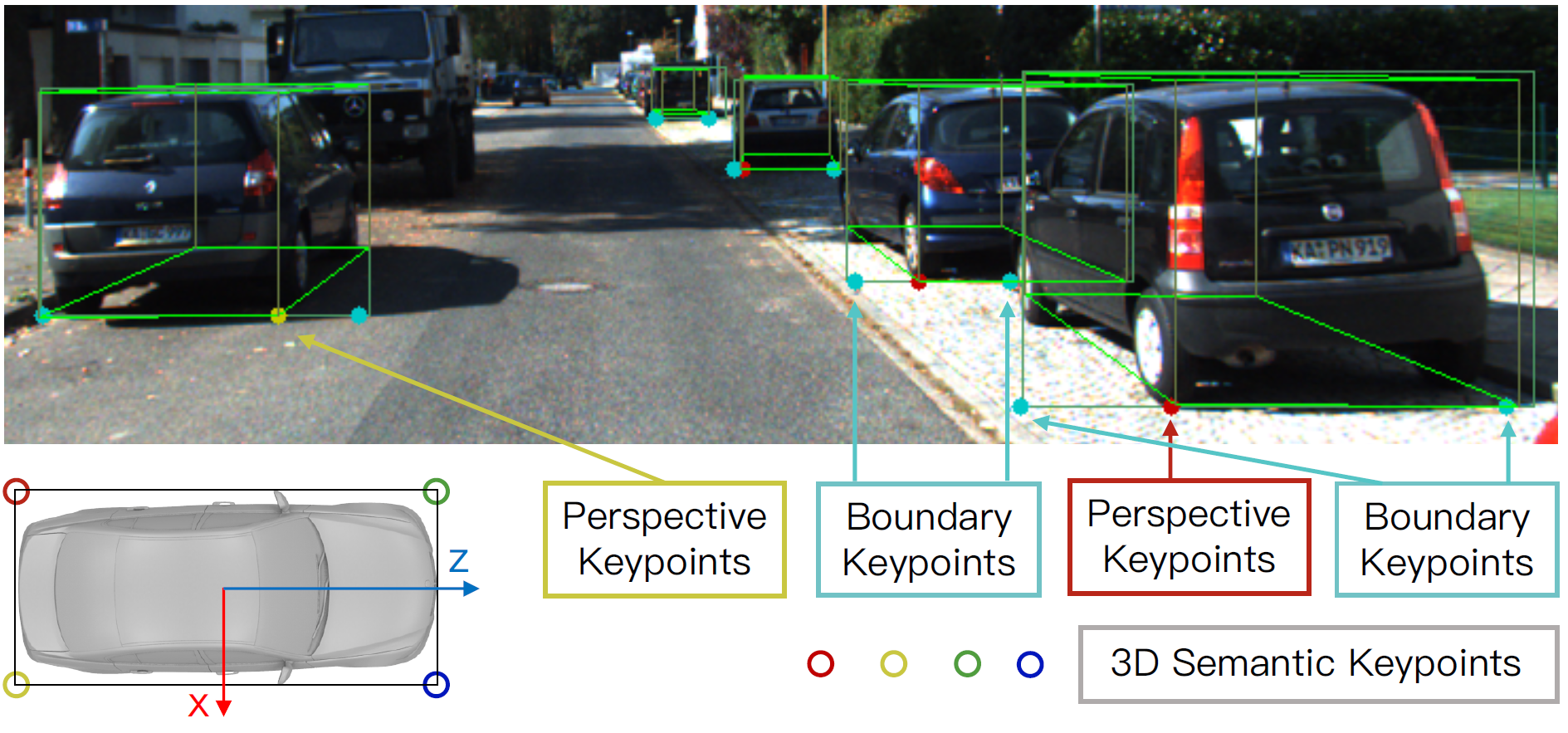
- Keypoint Prediction
如图 4 所示，考虑 3D 框底部矩形的四个关键点，投影到图像平面后，最多只有一个关键点会在图像 2D 矩形框内。对左目图像进行关键点预测，类似 Mask R-CNN，在 6×28×28 的基础上，因为关键点只有图像坐标 u 方向才提供了额外的信息，所以对每列进行累加，最终输出 6×28 的向量。前 4 个通道代表每个关键点作为 perspective keypoint 投影到该 u 坐标下的概率；后 2 个通道代表该 u 坐标是左右边缘关键点(boundary keypoints)的概率。为了找出 perspective keypoint，softmax 应用于 4×28 的输出上；为了找出左右边缘关键点，softmax 分别应用于后两个 1×28 的输出上。训练的时候，4×28 中只有一个被赋予 perspective keypoint，忽略没有 perspective keypoint 的情况（遮挡等），然后最小化 cross-entropy loss；对于边缘关键点，则分别最小化 1×28 维度上的 cross-entropy loss，前景中也会被赋予边缘关键点。
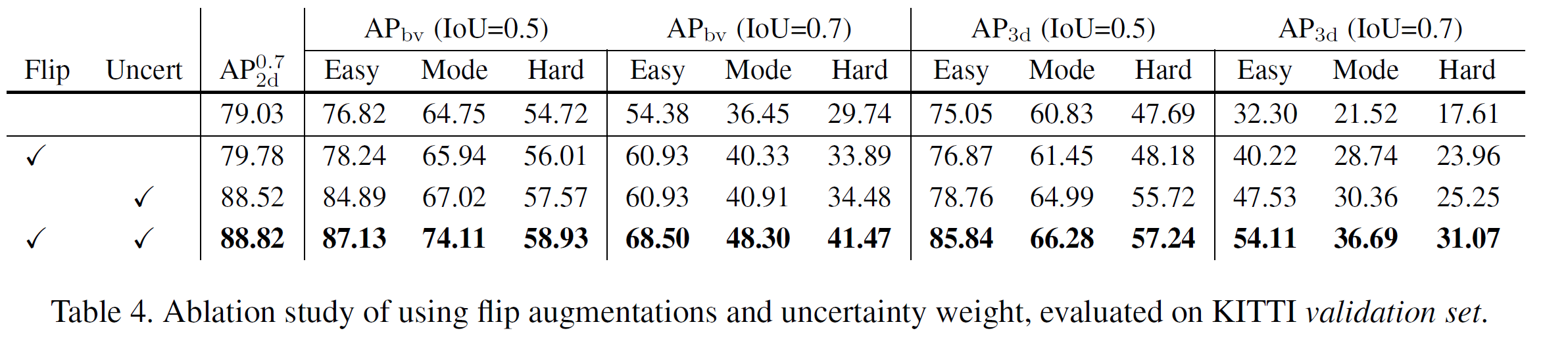
2. 3D Box Estimation
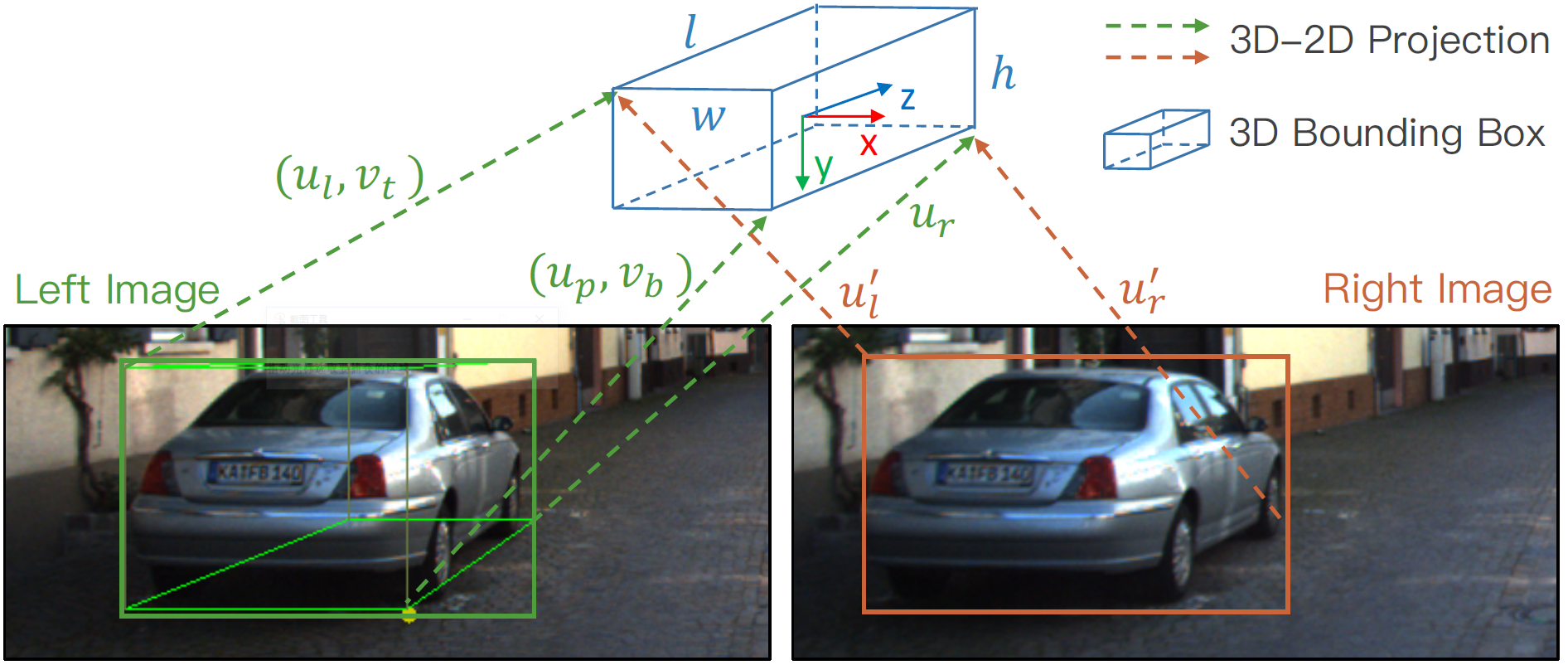已知关键点，2D 框，尺寸，朝向角，我们可以求解出 3D 框 \(\{x,y,z,\theta\}\)。求解目标是最小化 3D 框投影到 2D 框以及关键点的误差。如图 5 所示，已知 7 个观测量 \(z = \{u_l,v_t,u_r,v_b,u_l',u_r',u_p\}\)，分别代表左目 2D 框的左上坐标，右下坐标，右目 2D 框的左右 u 方向坐标，以及 perspective keypoint 的 u 方向坐标。在图 5 的情况下（其它视角下，注意符号变化），左上点投影关系如下： \[\require{cancel}
\begin{bmatrix}
u_l\\
v_t\\
1\\
\end{bmatrix}=K\cdot
\begin{bmatrix}
x_{cam}^{tl}\\
y_{cam}^{tl}\\
z_{cam}^{tl}\\
\end{bmatrix}\doteq \xcancel{K} \cdot T_{cam}^{obj} \cdot
\begin{bmatrix}
x_{obj}^{tl}\\
y_{obj}^{tl}\\
z_{obj}^{tl}\\
\end{bmatrix}=\begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}+
\begin{bmatrix}
cos\theta & 0 &sin\theta\\
0 & 1 & 0\\
-sin\theta & 0 & cos\theta\\
\end{bmatrix} \cdot
\begin{bmatrix}
-\frac{w}{2}\\
-\frac{h}{2}\\
-\frac{l}{2}\\
\end{bmatrix}\] 其中 \(K\) 为相机内参，\(T_{cam}^{obj}\) 为目标中心坐标系在相机坐标系下的表示，\((\cdot)_{cam/obj}\) 分别为点在相机坐标系，目标中心坐标系下的表示。同样的，这个视野下，右下点为： \[\require{cancel}
\begin{bmatrix}
u_r\\
v_b\\
1\\
\end{bmatrix}=K\cdot
\begin{bmatrix}
x_{cam}^{tl}\\
y_{cam}^{tl}\\
z_{cam}^{tl}\\
\end{bmatrix}\doteq \xcancel{K} \cdot T_{cam}^{obj} \cdot
\begin{bmatrix}
x_{obj}^{tl}\\
y_{obj}^{tl}\\
z_{obj}^{tl}\\
\end{bmatrix}=\begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}+
\begin{bmatrix}
cos\theta & 0 &sin\theta\\
0 & 1 & 0\\
-sin\theta & 0 & cos\theta\\
\end{bmatrix} \cdot
\begin{bmatrix}
\frac{w}{2}\\
\frac{h}{2}\\
-\frac{l}{2}\\
\end{bmatrix}\] 右目两个边缘点以及 perspective keypoint 点也可同样得到，由此可整理出 7 个方程组（论文中第一个公式符号有错）： \[\left\{\begin{array}{l}
u_l=(x- \frac{w}{2} cos\theta- \frac{l}{2} sin\theta) / (z+ \frac{w}{2} sin\theta - \frac{l}{2} cos\theta)\\
v_t=(y- \frac{h}{2}) / (z+ \frac{w}{2} sin\theta - \frac{l}{2} cos\theta)\\
u_r=(x+ \frac{w}{2} cos\theta+ \frac{l}{2} sin\theta) / (z- \frac{w}{2} sin\theta + \frac{l}{2} cos\theta)\\
v_b=(y+ \frac{h}{2}) / (z- \frac{w}{2} sin\theta + \frac{l}{2} cos\theta)\\
u'_l=(x-b- \frac{w}{2} cos\theta- \frac{l}{2} sin\theta) / (z+ \frac{w}{2} sin\theta - \frac{l}{2} cos\theta)\\
u'_r=(x-b+ \frac{w}{2} cos\theta+ \frac{l}{2} sin\theta) / (z- \frac{w}{2} sin\theta + \frac{l}{2} cos\theta)\\
u_p=(x+ \frac{w}{2} cos\theta- \frac{l}{2} sin\theta) / (z- \frac{w}{2} sin\theta - \frac{l}{2} cos\theta)\\
\end{array}\right.\] 其中 \(b\) 为双目的基线长(baseline)。以上方程组可用 Gauss-Newton 法求解。
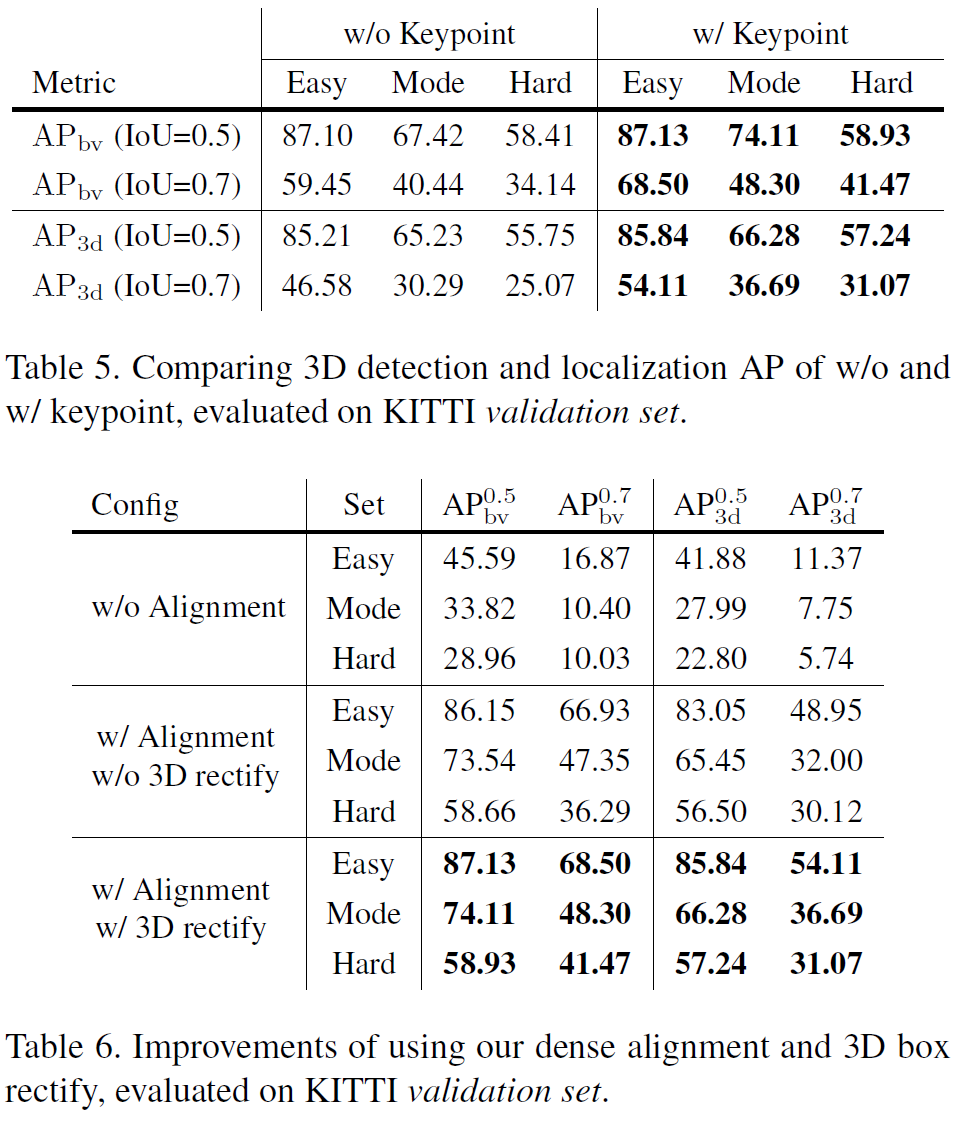
3. Dense 3D Box Alignment
以上得到的目标 3D 位置是 object-level 求解得到的，利用像素信息，还可以进行优化精确求解。首先在图像 2D 目标框内扣取一块 RoI，要使 RoI 能较为确定的在目标上，扣取方式定义为：
- 目标一半以下区域；
- perspective keypoint 与边缘关键点包围区域；
关键点预测的时候只预测了 u 方向的坐标，边缘关键点无 v 方向的信息，看起来会使某些背景像素被划入为目标像素，更好的方法是加入 instance segmentation 信息。定义误差函数为： \[E=\sum_{i=0}^N e_i=\sum_{i=0}^N \left\| I_l(u_i,v_i)-I_r(u_i-\frac{b}{z+\Delta z_i},v_i)\right\|\] 可由三角测量关系 \(z=\) 推出。上式中，\(z_i=z_i-z\) 表示某个像素点 \(i\) 所对应的 3D 点与目标中心点之间的距离。最小化总误差即可求得最优的中心点距离 \(z\)。优化过程可以用 coarse-to-fine 的策略，先以 0.5m 的精度找 50 步，再以 0.05m 的精度找 20 次。
这个 dense alignment 模块是独立的，可以应用到任意的左右目 3D 检测的后处理中。因为目标 RoI 是物理约束，所以这个方法避免了深度估计中不连续、病态的问题，且对光照是鲁棒的，因为每个像素都会对估计起作用。这里，本文只做了中心点的 align，尺寸，甚至朝向角是否能加入优化?
4. Other Details
[1] Li, Peiliang, Xiaozhi Chen, and Shaojie Shen. "Stereo R-CNN based 3D Object Detection for Autonomous Driving." arXiv preprint arXiv:1902.09738 (2019).
