点云注册是是点云数据处理中非常重要的一个方向。Object Registration with Point Cloud 中描述了基于点云的目标注册方法，主要阐述了传统 ICP 原理以及基于深度学习进行目标注册(相对位姿估计)的方法。本文[1]则详细介绍整个点云注册方法的类别与细节。
1. Problem Definition
假设两个点云集 \(X\in\mathbb{R} ^ {M\times 3}, Y\in\mathbb{R} ^ {N\times 3}\)，其中每个点表示为 \(\mathbf{x} _ i(i\in [1,M])\)，\(\mathbf{y} _ i(y\in [1,N])\)。两个点云集合中有 \(K\) 个匹配点对，点云注册问题就是找到参数 \(g\)，即旋转矩阵 \(R\in\mathcal{SO}(3)\) 和位移矩阵 \(t\in\mathbb{R} ^ 3\)，使得： \[\mathop{\arg\min}\limits _ {R\in\mathcal{SO}(3),t\in\mathbb{R} ^ 3}\Vert d(X,g(Y))\Vert ^ 2 _ 2 \tag{1}\] 其中 \(d(X,g(Y))=d(X,RY+t)=\sum _ {k=1} ^ K \Vert \mathbf{x} _ k-(R\mathbf{y} _ k+t)\Vert _ 2\)。这个问题是典型的鸡生蛋蛋生鸡问题，如果匹配点对已知，那么变换矩阵可以求解；如果变换矩阵已知，那么就能得到匹配点对。
2. Challenges
根据数据源类型，点云注册可分为 same-source 以及 cross-source 两类。其挑战分别有：
- Same-source
- Noise and Outliers
- Partial overlap
- Noise and Outliers
- Cross-source
- Noise and Outliers
- Partial overlap
- Density difference
不同传感器获得的数据源，点云密度可能不一样。 - Scale variation
不同传感器获得的数据源，点云的空间尺度可能不一样。
- Noise and Outliers
3. Categories
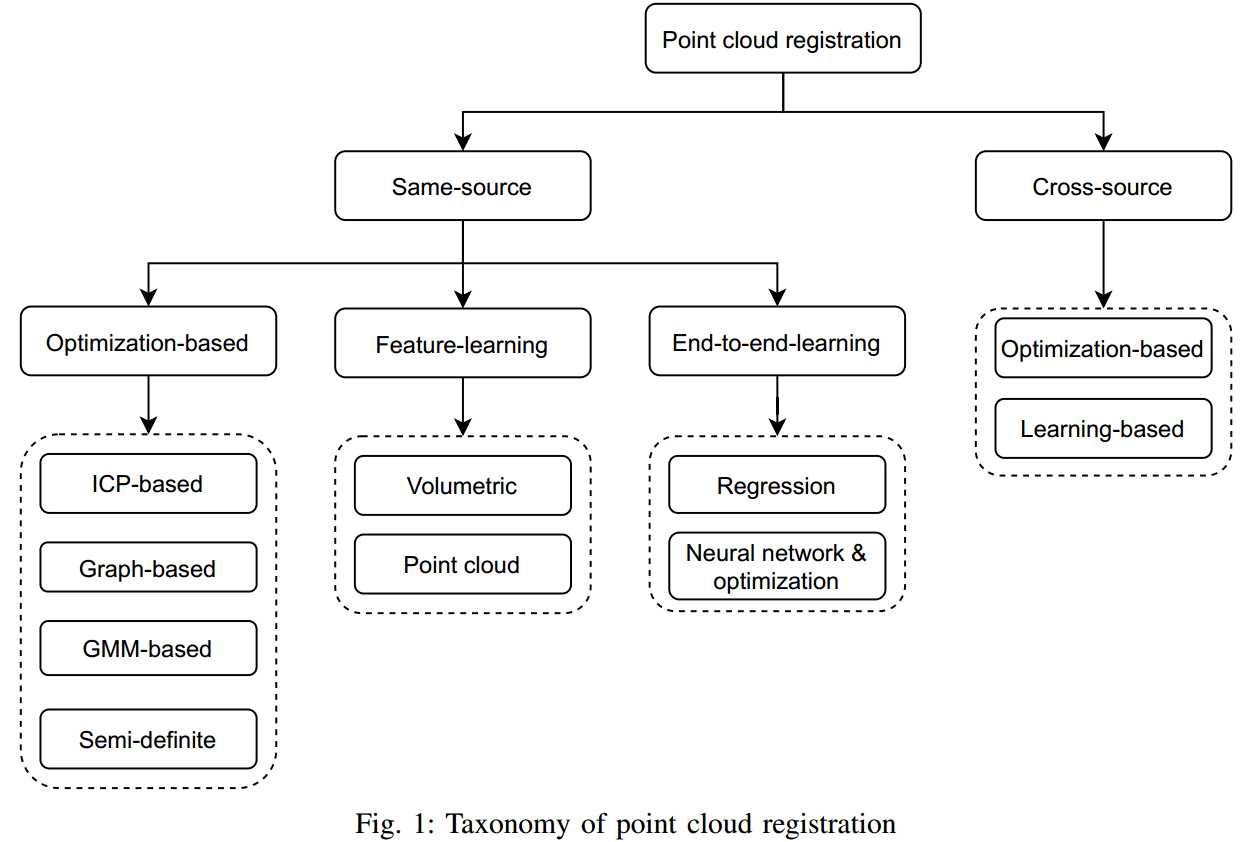
- Optimisation-based
- Feature learning
- End-to-end learning-based
- Cross-source registration
4. Optimisation-based
大多数优化方法都包含两个步骤：匹配点对搜索，以及转换矩阵估计。匹配点对可通过计算 point-point 距离或特征相似度得到。这种方法的好处是有严谨的数学解，能保证收敛，不需要训练数据；缺点是需要复杂的策略来解决噪音，离群点，遮挡等问题。
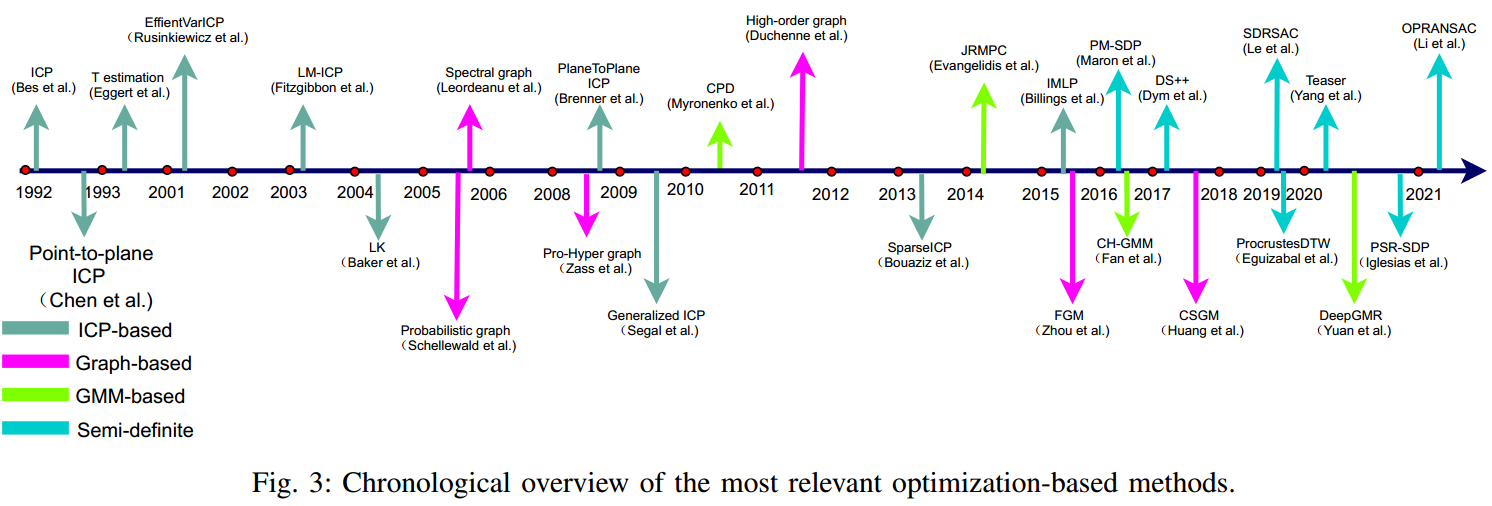对于已搜索到匹配点对后，可用非线性问题求解方法来优化计算转换矩阵。根据优化策略不同，可分为如下几种方法。
4.1. ICP-based
首先匹配点中距离度量方式分为三种：
Point-Point
就是式 (1) 下方的传统方式，计算两个点的欧式距离。Point-Plane
表示点与对应平面之间的距离： \[\mathop{\arg\min}\limits _ {R\in\mathcal{SO}(3),t\in\mathbb{R} ^ 3}\left\{\sum _ {k=1} ^ K w _ k\left\Vert \mathrm{n} _ k * (\mathrm{x} _ k-(R\mathrm{y} _ k+t))\right\Vert ^ 2\right\} \tag{2}\] 其中 \(w _ k\) 是匹配对权重，\(\mathrm{n _ k}\) 是面的法向量。Plane-Plane
表示面与对应平面之间的距离： \[\mathop{\arg\min}\limits _ {R\in\mathcal{SO}(3),t\in\mathbb{R} ^ 3}\left\{\sum _ {k=1} ^ K \left\Vert \mathrm{nx} _ k-(R\mathrm{ny} _ k+t)\right\Vert ^ 2\right\} \tag{3}\] 其中 \(\mathbf{nx,ny}\) 是对应的法向量。Generalized ICP
\[\mathop{\arg\min}\limits _ {T}\left\{\sum _ {k=1} ^ K \left\Vert d ^T(C _ k ^ Y+\mathbf{T} C _ k ^ X\mathbf{T} ^ T) ^ {-1}\right\Vert ^ 2\right\} \tag{4}\] 其中 \(\{C _ k ^ X\}\)，\(\{C _ k ^ Y\}\) 为点云 \(X,Y\) 之间的协方差矩阵。当 \(\{C _ k ^ X=0\}\)，\(\{C _ k ^ Y=I\}\) 时，就是标准的 point-point ICP；\(\{C _ k ^ X = 0\}\)，\(\{C _ k ^ Y = P _ k ^ {-1}\}\) 时就是 pont-plane ICP，其中 \(P _ k ^ {-1}\) 为法向量。
根据匹配点度量方式获得匹配点后，即可优化求解位姿矩阵，有三种方法：SVD-based
用奇异值分解的方式求解。Lucas-Kanade
包括 Levenberg-Marquardt 方法，用雅克比矩阵及近似高斯牛顿法优化求解。Procrustes analysis
将位姿估计转换为线性最小二乘问题。位姿闭式解为 \(P=(X _ 2 ^ HX _ 1)^ { -1 }X _ 2^Hx _ 1\)。
4.2. Graph-based
将点云建模为非参图模型，包括边与顶点。GM 方法目的就是通过边与顶点去寻找两个图中的匹配点，GM 可分为 second-order 与 high-order 方法，前者只考虑边与边，顶点与顶点的相似性，后者则会考虑多于两个点的相似性，比如三角对相似性。
4.3. GMM-based
高斯混合模型法核心是将点云注册问题建模为最大化似然的过程。求解后，可得到位姿和混合高斯参数。
4.4. Semi-definite Registration
将问题近似为其它问题求解。
5. Feature-learning
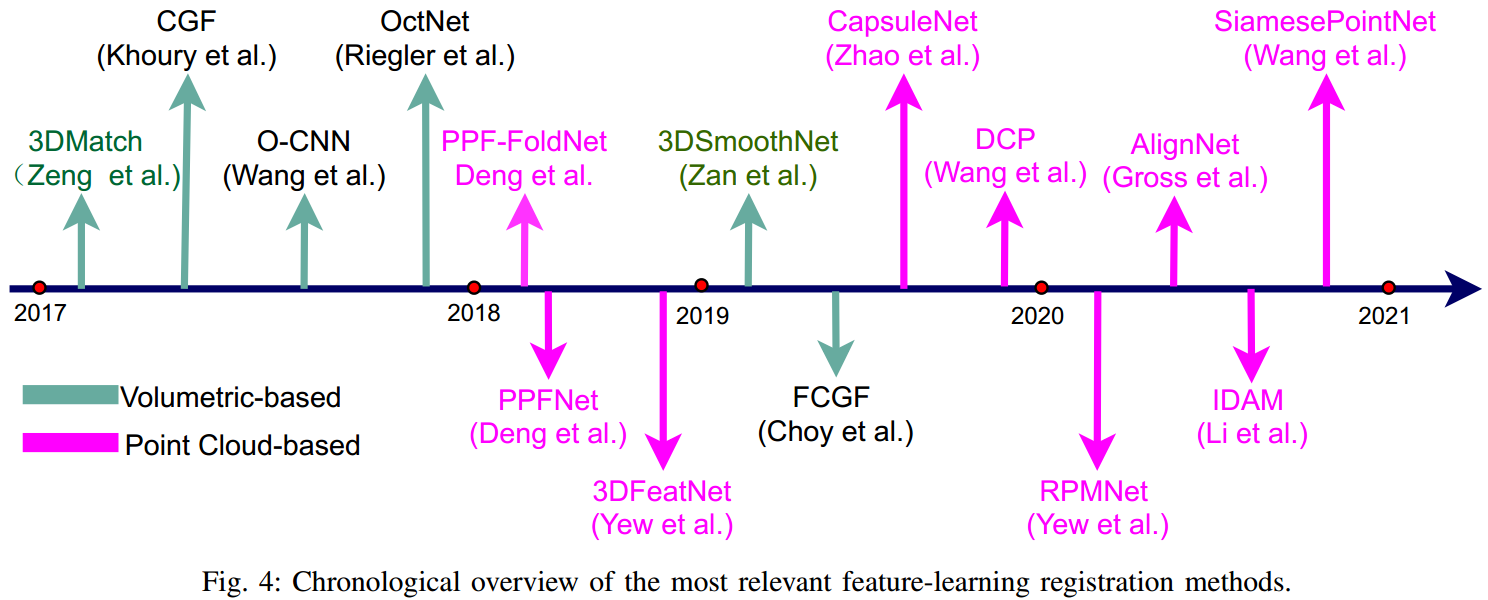基于特征学习的方法，是提取点云的点级别特征，然后作一次性精准匹配，最后直接用 SVD 等后端优化方法得到，无需进行多次迭代。Object Registration with Point Cloud 中介绍的也属于这种方法。
对于点云特征提取的方法，Learning on volumetric data 以及 Learning on point cloud 都介绍的已经非常多了，这里不作展开。
6. End-to-end Learning-based
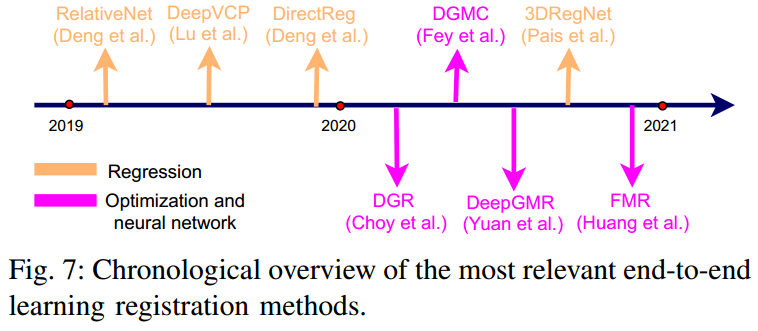如图 4. 所示，端到端的方法主要分为 Registration by regression 和 Registration by optimization and neural network 方法。
7. Cross-source
如图 5. 所示，多源点云数据的注册，方法也分为 Optimization-based 和 Learning-based，思路也差不多，这里不作展开。
3. Reference
[1] Huang, Xiaoshui, et al. "A comprehensive survey on point cloud registration." arXiv preprint arXiv:2103.02690 (2021).
