概率目标检测是将不确定估计应用于目标检测任务中，不确定性估计之前已经描述很多了，包括 Epistemic Uncertainty，Aleatoric Uncertainty，以及 Uncertainty Calibration 相关技术。本文[1]则详细阐述概率目标检测的进展。
在自动驾驶领域，不管是什么传感器，在极端天气环境或不熟悉的场景下，以及远距离或高遮挡情况下，基于深度学习的目标检测模型失效概率会比较大，或者说预测的不确定性会比较大。人类驾驶员在这方面比较擅长，比如在雨夜看不太清的场景，会先降低速度，增加观察时间，以获得观测的高确定性。所以对网络而言，不确定的估计才能为后续增加观测的确定性作准备。
1. Uncertainty Estimation in Deep Learning
Perception Uncertainty in Deep Learning 中已经较为详细得阐述了 Uncertainty 的来龙去脉。贝叶斯神经网络框架下，不确定性可分解为认知不确定性(Epistemic Uncertainty)以及偶然不确定性(Aleatoric Uncertainty)。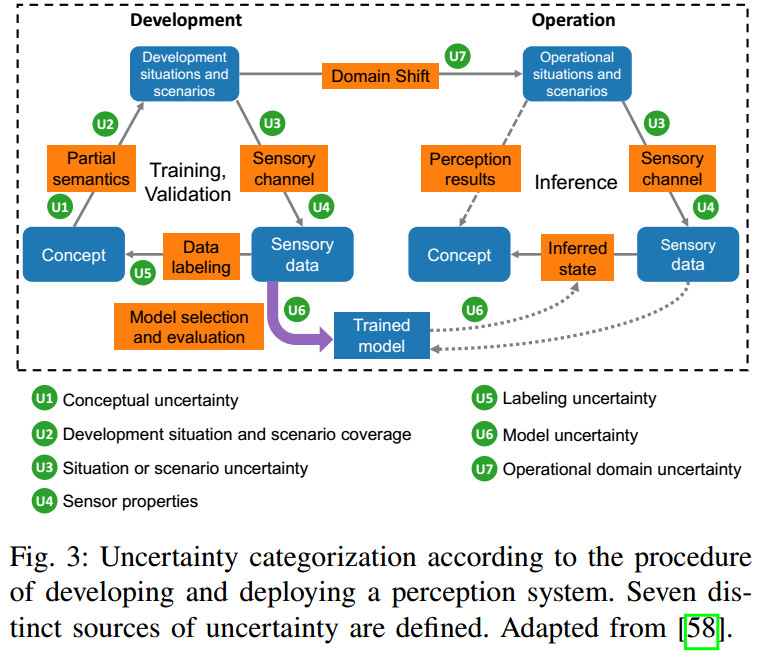 
从感知数据流角度，如图 1. 所示，会引入很多不确定性，从最原始的传感器不确定性，到标注不确定性，再到模型训练测试的不确定性，所有这些不确定性构成了最终模型输出结果的不确定性。
数学上，对于训练数据集 \(\mathscr{D}\) 贝叶斯神经网络的输出分布表示为: \[p(\mathbf{y|x}, \mathscr{D}) = \int p(\mathbf{y|x}, \mathbf{W})p(\mathbf{W}| \mathscr{D}) \mathrm{d}\mathbf{W}\tag{1}\] 其中 \(p(\mathbf{y|x,W})\) 表示观测似然，包含了偶然不确定性；\(p(\mathbf{W}|\mathscr{D})\) 表示模型后验分布，包含认知不确定性。
1.1. Practical Methods for Uncertainty Estimation
实际不确定性的估计需要在效率上考虑到其可行性。可分为用于估计模型认知不确定性的 MC-Dropout，Deep Ensembles 方法；用于估计偶然不确定性的 Direct Modeling 方法；以及用于估计模型认知及偶然不确定性的 Error Propagation 方法，以下作详细描述：
Monte-Carlo Dropout
对网络进行 \(T\) 次前向 Inference，\(\mathbf{W} _ t\) 为网络经过 dropout 后的权重，那么网络预测的概率分布为： \[p(\mathbf{y|x},\mathscr{D})\approx \frac{1}{T}\sum _ {t=1} ^ T p(\mathbf{y|x,W _ t}) \tag{2}\] 对于回归问题，由此可计算其回归量的均值和方差。Deep Ensembles
用网络模型集合来估计输出的概率分布，本质上 Monte-Carlo Dropout 方法也是一种网络模型集合的方法。设 \(M\) 个网络权重为 \(\{\mathbf{W} _ m\} _ {m=1} ^ M\)，那么输出概率分布为： \[p(\mathbf{y|x},\mathscr{D})\approx \frac{1}{M}\sum _ {m=1} ^ M p(\mathbf{y|x,W _ m}) \tag{3}\]Direct Modeling
该方法假设模型的回归输出符合多模态混合高斯分布，即 \(p(y|\mathbf{x,W}) = \mathcal{N}(y|\hat{\mu}(\mathbf{x,W}),\hat{\sigma} ^ 2(\mathbf{x,W}))\)，其中 \(\hat{\mu}(\mathbf{x,W})\) 为网络输出，\(\hat{\sigma} ^ 2(\mathbf{x,W})\) 为输出值的方差。最小化负对数似然函数，即可预测输出量的均值和方差： \[L(\mathbf{x,W})=-\mathrm{log}(p(\mathbf{y|x,W})) \approx \frac{(y-\hat{\mu}(\mathbf{x,W}))^2}{2\hat{\sigma} ^ 2(\mathbf{x,W})}+\frac{\mathrm{log}\hat{\sigma} ^ 2(\mathbf{x,W})}{2}\tag{4}\] 对于分类问题，假设 softmax 预测中的每个 logits 元素符合独立高斯分布，类似回归问题，网络同时预测均值 logits 以及方差 logits。训练的时候，用重采样的方法在每个高斯分布中采样出每个 logits，最后再用标准的分类误差函数计算其损失函数。
直接模型求解只需要增加额外的模型分支即可，引入的计算量并不大，但是会产生预测的方差不准的问题，需要进一步标定。Error Propagation
误差传递方法计算效率最高，直接将数据源的误差通过每个操作层进行传递，比如 A General Framework for Uncertainty Estimation in Deep Learning。
1.2. Evaluation and Benchmarking
评估不确定性估计的指标有：
Shannon Entropy
用来描述分类任务的不确定性： \[\mathcal{H}(y|\mathbf{x},\mathscr{D}) = -\sum _ {c=1} ^ C p(y=c|\mathbf{x},\mathscr{D})\mathrm{log}\left(p(y=c|\mathbf{x},\mathscr{D})\right) \tag{5}\] 当 \(p(y=c|\mathbf{x},\mathscr{D}) = 0 \mathrm{or} 1\) 时，不确定性最小。个人认为，该指标只能描述不确定性的大小，无法描述不确定估计的准确性。Mutual Information
与 SE 类似，也是描述分类任务的不确定性，但是引入了模型不确定性： \[\mathcal{I}(y,\mathbf{W|x},\mathscr{D})=\mathcal{H}(y|\mathbf{x},\mathscr{D})-\mathbb{E} _ {p(\mathbf{W}|\mathscr{D})}\left[\mathcal{H}(y|\mathbf{x,W})\right] \tag{6}\] 其中 conditional Shannon Entropy 通过采样模型权重(MC-Dropout)计算得到： \[\mathcal{H}(y|\mathbf{x,W}) = -\sum _ {c=1} ^ C p(y=c|\mathbf{x,W})\mathrm{log}\left(p(y=c|\mathbf{x,W})\right) \tag{7}\]Calibration Plot
Uncertainty Calibration 中已经较为详细的阐述了 Calibration Plot 的作用，这里不作展开。由此可用 ECE Score 来评估不确定的准确度： \[\mathrm{ECE}=\sum _ {t=1} ^ T\frac{N _ t}{N _ {eval}}|p _ t-\hat{p} _ t| \tag{8}\]Negative Log Likelihood(NLL)
NLL 也是 Direct Modeling 方法中不确定性的预测的 Loss，其描述了预测的概率分布与真值分布的相似性，所以能评估不确定性预测的准确度： \[\mathrm{NLL}=-\sum _ {n=1} ^ {N _ {test}}\mathrm{log}\left(p(\mathbf{y _ n|x _ n}, \mathscr{D})\right) \tag{9}\]Brier Score
用于评估分类概率的准确性: \[\mathrm{BS} = \frac{1}{N _ {test}}\sum _ {n=1} ^ {N _ {test}}\sum _ {c=1} ^ C (\hat{s} _ {n,c} - y _ {n,c}) ^ 2 \tag{10}\] 其中 \(\hat{s} _ {n,c}\) 表示 softmax score, \(y _ {n,c}\in\{0, 1\}\) 表示真值。越小表示估计的不确定性越好。Error Curve
不确定性越大，表示与真值的误差越大。所以逐步去掉不确定性较大的数据，剩下数据的误差会逐渐减少。Total Variance(TV)
在回归任务中，计算 Covariance matrix 的 trace，作为回归任务的总的方差。
2. Probabilistic Object Detection
传统的目标检测方法都是确定性的，而 POD 目的是在目标检测的基础上，在分类及回归任务中，进一步估计可靠的不确定性。
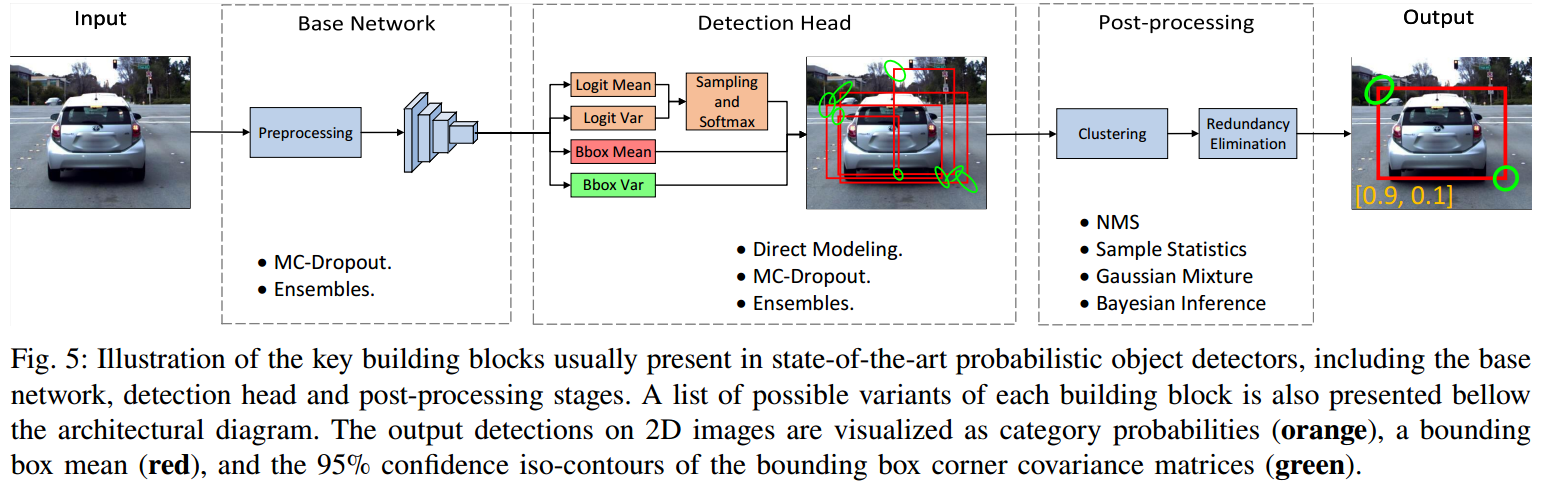我们要估计的不确定性包括 Epistemic Uncertainty 以及 Aleatoric Uncertainty。认知不确定性用 MC-Dropout 来估计。偶然不确定性中的回归问题在 Heteroscedastic Aleatoric Uncertainty 中已经较为详细的描述，基本就是用 NLL LOSS 来优化；对于分类问题，本文采用重采样高斯分布的 softmax logits 的方法，具体的，预测输出与分类 softmax logits 长度一样的 logits variance，然后对每个高斯分布的 logit 作重采样，作为最终的输出以作 Loss 优化。
综上，POD 估计不确定性可归纳为： \[\left\{\begin{array}{l}
\hat{\mu}(\mathbf{x}) = \frac{1}{T}\sum _ {t=1} ^ T(\mathbf{x,W} _ t) \\
\hat{\sigma} ^ 2(\mathbf{x}) = \hat{\sigma} _ e ^ 2(\mathbf{x}) + \hat{\sigma} _ a ^ 2(\mathbf{x}) \\
\hat{\sigma} _ e ^ 2(\mathbf{x}) = \frac{1}{T}\sum _ {t=1} ^ T\left(\hat{\mu}(\mathbf{x,W} _ t)\right) ^ 2 - \left(\hat{\mu}(\mathbf{x})\right) ^ 2\\
\hat{\sigma} _ a ^ 2(\mathbf{x}) = \frac{1}{T} \sum _ {t=1} ^ T \hat{\sigma} ^ 2(\mathbf{x,W} _ t)
\end{array}\tag{11}\right.\] 通过 T 次蒙特卡洛采样，得到最终总的不确定性。
3. Comparative Study
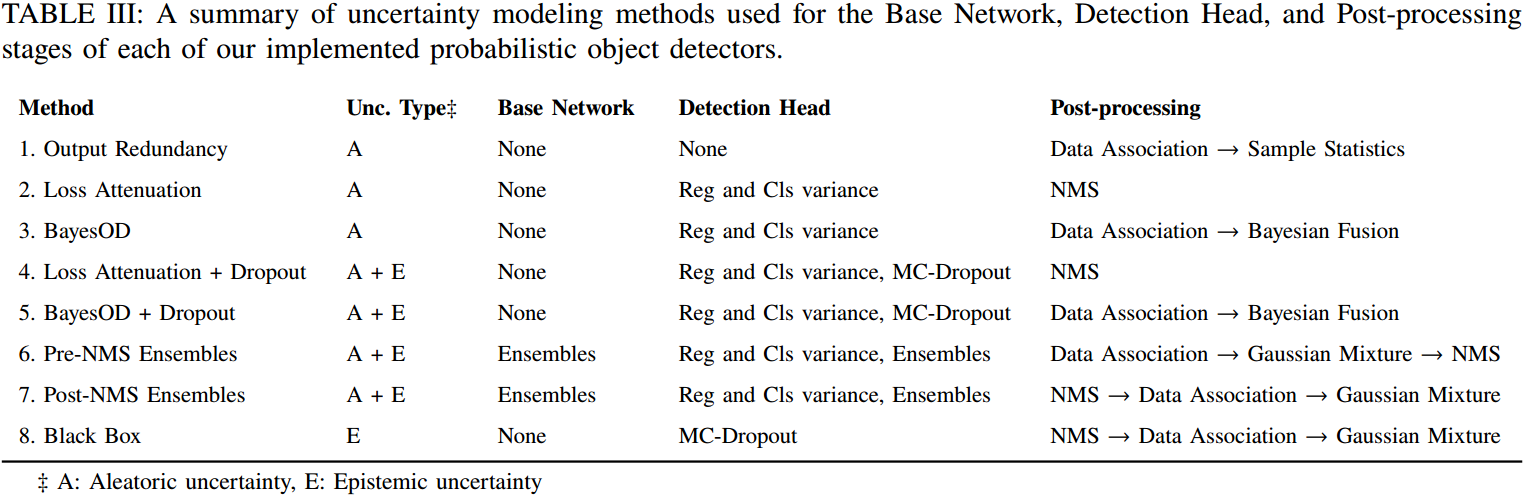用 Droupout 估计 Epistemic Uncertainty，对于 Aleatoric Uncertainty 的估计，实现了三种方法：
Loss Attenuation
网络输出分类 logits 以及回归量的均值和方差，用 Direct Modeling 中的权重 Loss 来优化；BayesOD
与 Loss Attenuation 不同的是，后处理用 Data Association + Bayesian Fusion 来代替标准的 NMS 算法；Output Redundancy
网络输出不作改变，后处理采用 Data Association + Sample Statistics 来估计不确定性；
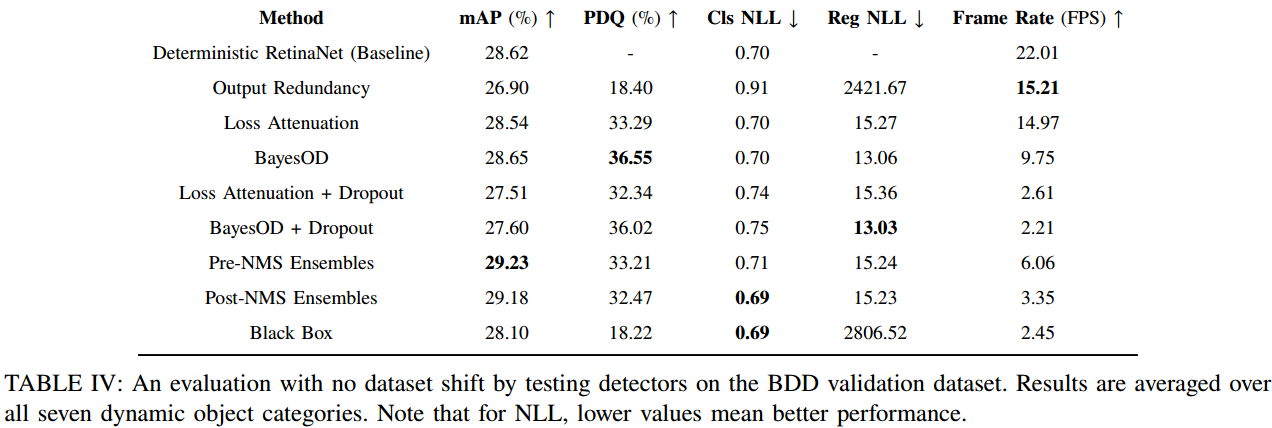这几种方法对比如图 4. 所示，不确定性估计对目标检测性能有所提升，并且能提供预测的不确定性。具体方法的实现细节可见[2]。
4. Reference
[1] Feng, Di, et al. "A Review and Comparative Study on Probabilistic Object Detection in Autonomous Driving." arXiv preprint arXiv:2011.10671 (2020).
[2] https://github.com/asharakeh/pod_compare
