Anchor-Free Detection

　　3D 目标检测的技术思路大多数源自 2D 目标检测，所以图像 2D 检测的技术更迭极有可能在将来影响 3D 检测的发展。目前 3D 检测基本还是 Anchor-Based 方法(也称为 Top-Down 方法)，而今年以来，Anchor-Free(也称为 bottom-Up 法) 的 2D 检测已经达到了 SOTA，所以本文来探讨下 Anchor-Free 的目标检测方法发展历程。
　　如图 1. 所示(图片出自https://zhuanlan.zhihu.com/p/82491218)，每种技术思路的发展都是为了解决目标检测中的一些痛点，这些技术思路又交相互用，才推动目标检测往更简单、更高性能方向发展。列举一些主要的痛点：

• 正负样本不均衡及无法区分困难样本导致网络学习困难，two-stage;
• 网络及后处理复杂，one-stage，包含 Anchor-Free 方法；
• 尺度问题很难同时检测大小目标，pyramid-scale；
• 框与特征的对齐问题导致提取出的目标特征有偏差，deformable；

　　本文包含两大块，一块是 Anchor-Free 方法的概括总结，另一块是代表算法的详细分析。

1. 归纳总结

　　首先推荐下乃爷写的文章——聊聊 Anchor 的“前世今生”，高屋建瓴。本节也是打算聊聊 Anchor-Free 方法的来龙去脉，以及归纳总结下各算法的思路。
　　由之前讨论的，其中一个比较大的问题是，目标检测中正负样本严重不平衡。这会导致网络学习时很难针对性的学习困难样本，而 two-stage 相比 one-stage 多了一级正样本的删选，所以在没有额外困难样本选择策略的情况下，two-stage 普遍比 one-stage 效果好。可以想象的是，更多 stage 这种级联结构效果会更好，但是网络会变得相当复杂。这个痛点极大地阻碍了 one-stage 以及 Anchor-Free(负样本更多) 方法的发展，OHEM 困难样本学习当然是种有效的方法，但是还不够，直到 RetinaNet 中 Focal Loss 的提出，有效解决了正负样本严重不均衡所导致的学习困难问题。由此不仅 Anchor-based one-stage 方法性能达到了 two-stage 高度，甚至 Anchor-Free 方法性能也达到了 SOTA。
　　回顾 Anchor-Free 检测，最早的应该是 YOLO-v1^[1]，DenseBox^[2]，而 RetinaNet^[3] 中 Focal Loss 的提出，使得 Anchor-Free 方法引来爆发式发展。大体上可分为两种：

1. 回归目标角点，后处理需要匹配角点以生成目标框，以 CornerNet^[4] 为代表的一系列改进方法 CornerNet-Lite^[5]，CenterNet(KeyPoint Triplets)^[6]，ExtremeNet^[7]等；
2. 像素级别预测目标框的不同编码量，后处理很容易生成目标框，有 CenterNet(Objects as Points)^[8]，FCOS^[9]，FoveaBox^[10]，FSAF^[11]等；

回归角点的方法继承了人体姿态估计的很多策略，backbone 都使用 Hourglass^[14] 网络，在单尺度上能提取有效的特征；而像素级别预测目标框的不同编码量，引入了 FPN^[15] 网络进行多尺度检测，解决大小框在同一中心点或有相同角点的情况(CenterNet 还是使用了 Hourglass 网络，因为单尺度能很容易融合 3D 检测，人体姿态估计等任务)。此外，RepPoints^[12] 延续了 Deformable Conv 的工作，去掉了角点的框约束，使得角点一定贴合目标的边缘，本质上基本解决了以上所列的问题，其思想很值得借鉴。

2. CornerNet^[4], CornerNet-Lite^[5]

2.1. 网络结构

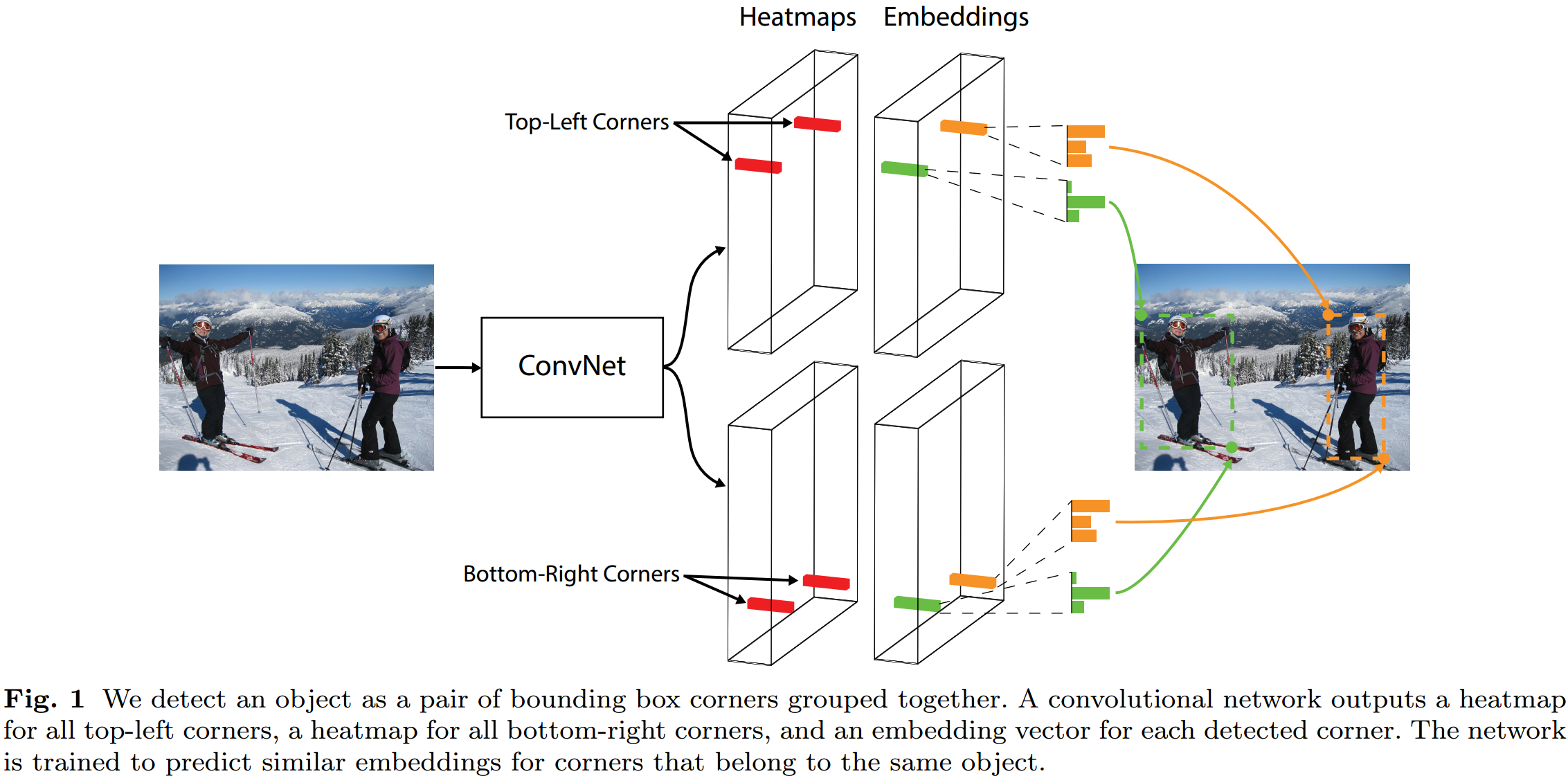
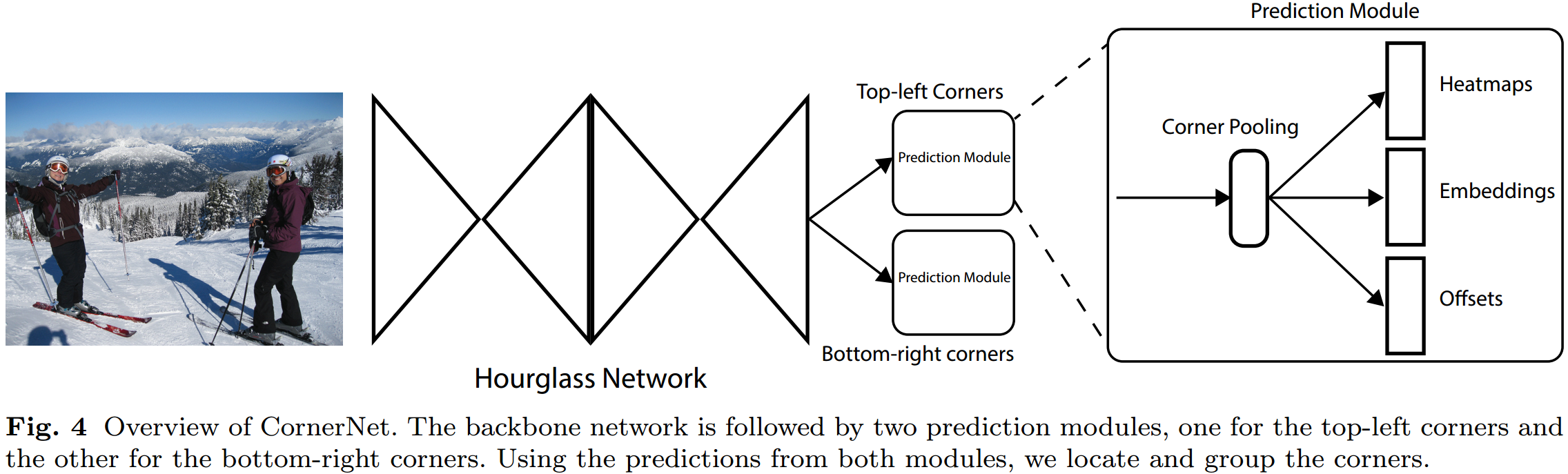　　如图 2.1 与 2.2 所示，CornerNet 的 backbone 采用了人体关键点检测中常用的 Hourglass 网络，这种沙漏网络类似多层 FPN，能有效提取细节信息；网络最终输出的是 Top-Left Corners Heatmaps，Bottom-Right Corners Heatmaps，以及对应的 Embeddings，Offsets。这里以 Top-Left Corners 分支为例，说明其网络计算过程。 　　如图 2.3. 所示，这里引入 Corner Pooling Module，该模块能提取角点的上下文信息，其计算过程是行最大值与列最大值的叠加。网络输出的:

• Score Heatmaps \(\in\mathbb{R}^{C\times H\times W}\)，每个 Channel 的监督项是个二值图，代表了是否是该类别下的角点；
• Embeddings \(\in\mathbb{R}^{C\times H\times W}\)，每个角点都会预测一个 Embedding 值(度量空间下的值)，用来对 top-left 与 bottom-right 角点的配对；
• Offsets \(\in\mathbb{R}^{2\times H\times W}\)，由于 \(H\times W\) 可能是原图的下采样，所以变换到原图的角点坐标会有离散偏差，需要预测 Offsets 修正，类别无关或者类别有关都可以；

Inference 阶段，得到这三个输出后，还需要进行后处理才能得到目标检测框。后处理过程为：

1. 对 Heatmaps 采用点 NMS 处理(可通过 \(3\times 3\) max-pooling 实现)得到分数最高的前 100 个 top-left 角点以及前 100 个 bottom-right 角点；
2. 类内计算 top-left 角点与 bottom-right 角点的 Embedding L1 距离，删除大于 0.5 的配对；
3. 通过 Offsets 调整配对的角点值；
4. 计算配对的角点值的平均分数，作为该目标框的分数；

相比 Anchor-based 方法，整个后处理还是相对较为简单，没有框之间的 IoU 计算。

2.2. Loss

　　网络训练的 Loss 表示为： \[ L= L_{det} + \alpha L_{pull} + \beta L_{push} + \gamma L_{off} \tag{2.1}\] 其中 \(L_{det}\) 是角点检测的 Loss 项，\(L_{pull}, L_{push}\)是 Embedding 距离监督项，\(L_{off}\)是 Offsets 的 Loss 项；\(\alpha,\beta,\gamma\)是权重。

• \(L_{det}\)
  角点检测是 pixel-level 的检测，每个角点虽然只有一个真值，但是靠近角点的像素点作为角点而构成的目标框与真值框重合度也会较高，所以在真值角点处设计高斯函数 \(e^ {-\frac{x^ 2+y^ 2}{2(r/3) ^ 2}}\) 作为标签衰减函数，\(r\) 值等于真值角点周围定义的圆的半径。圆半径由以下准则确定：四个角点为中心构成四个圆，在这区域内构成的目标框与真值框的 IoU 要小于 \(t\)(文中设为 0.3)。所以这里引入超参数 \(t\)。由此得到检测的 Loss 项： \[ L_{det} = -\frac{1}{N}\sum_{c=1}^C\sum_{i=1}^H\sum_{j=1}^W \left\{\begin{array}{l} (1-p_{cij})^{\alpha} \mathrm{log}(p_{cij}) & \mathrm{if} \; y_{cij}=1\\ (1-y_{cij})^{\beta} (p_{cij})^{\alpha} \mathrm{log}(1-p_{cij}) & \mathrm{otherwise} \end{array}\tag{2.2}\right.\] 其中 \(p_{cij}\) 代表 Heatmaps 中 \(c\) 类别的 \((i,j)\) 位置预测的角点分数，\(y_{cij}\) 表示经过高斯衰减后的真值标签值。可以看出这是 Focal Loss 的变种，对平衡正负样本及学习困难样本有重要作用。
• \(L_{off}\)
  原图点 \((x,y)\) 经过网络下采样后变换到 \((\lfloor\frac{x}{n}\rfloor,\lfloor\frac{y}{n}\rfloor)\)，与真值的 Offset 可表示为 \(\mathbf{o}_k=(\frac{x_k}{n}-\lfloor\frac{x_k}{n}\rfloor\, \frac{y_k}{n}-\lfloor\frac{y_k}{n}\rfloor)\)，由此可得 Offsets 的 Loss 项： \[ L_{off}=\frac{1}{N}\sum_{k=1}^N\mathrm{SmoothL1Loss}(\mathbf{o}_k,\mathbf{\hat{o}}_k) \tag{2.3}\]
• \(L_{pull}, L_{push}\)
  每个角点都会预测一个 Embedding 值，期望的是，同一个目标框的 top-left 角点与 bottom-right 角点的 Embedding 值要相近，不同框的角点的 Embedding 值差异要大，由此设计： \[\left\{\begin{array}{l} L_{pull} = \frac{1}{N}\sum_{k=1}^N\left[(e_{t_k}-e_k)^2+(e_{b_k}-e_k)^2\right] \\ L_{push} = \frac{1}{N(N-1)}\sum_{k=1}^N\sum_{j=1, j\not=k}^N\mathrm{max}(0,\Delta-|e_k-e_j|) \end{array}\tag{2.4}\right.\] 其中 \(e_{t_k}, e_{b_k}\) 分别表示 top-left 角点与 bottom-right 角点的 Embedding 值，\(e_k\) 是二者的平均值，\(\Delta\) 设定为 1。与 Offsets 一样，该 Loss 项也只作用于真值角点。

3. CenterNet: KeyPoint Triplets^[6]

3.1. 网络结构

　　CenterNet 的 Motivation是：CornerNet 的 corner pooling 对目标框内的特征提取能力有限，以及角点匹配得到的目标框在没有其它约束下有时候检测结果会出错。由此，如图 3.1 所示，CenterNet 在 CornerNet 基础上增加了 Center 的预测分支，并引入 center pooling 以及 cascade corner pooling 模块。
　　Inference 处理时，预测的 Center 点用于删除不合理的框。具体的，取 top-left 角点与 bottom-right 角点匹配后得到的目标框中心点，在中心点附近检测是否有 Center 点，如没有，则删除该匹配；否则，保留该目标框，并用这三个点的平均分数代表该目标框的分数。 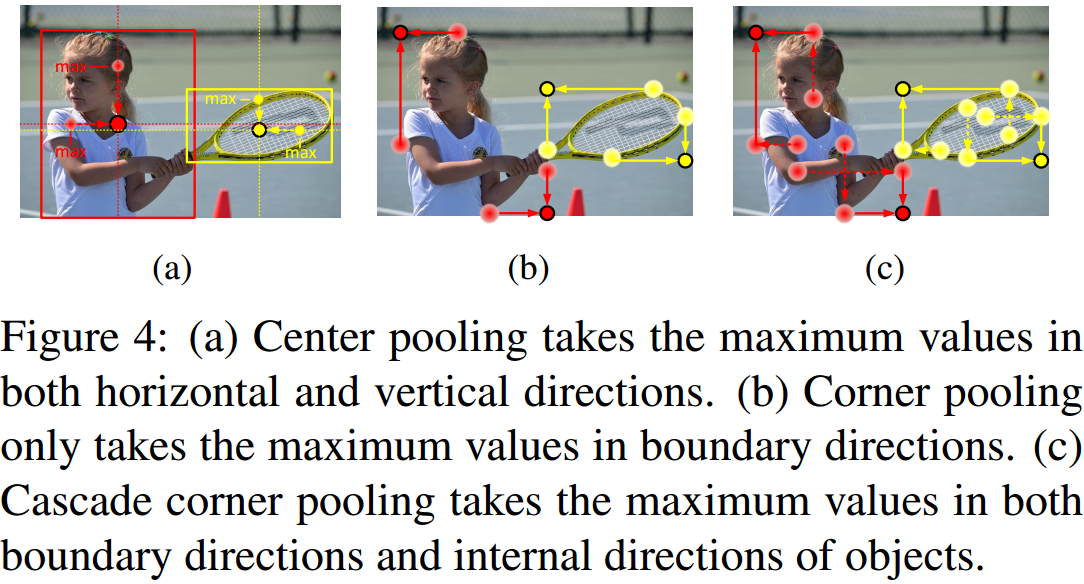　　如图 3.2 所示，CenterNet 引入 center pooling 并升级了 cascade corner pooling，这两个模块极大的提升了目标框内的特征提取融合能力，类似 ROI-pooling 的作用。具体的：

• Center Pooling，叠加了水平和垂直方向上的最大值；
• Cascade Corner Pooling，不同于 Corner Pooling 只在角点所在的目标框边缘处取最大值，它还在目标框的内部取得最大值；

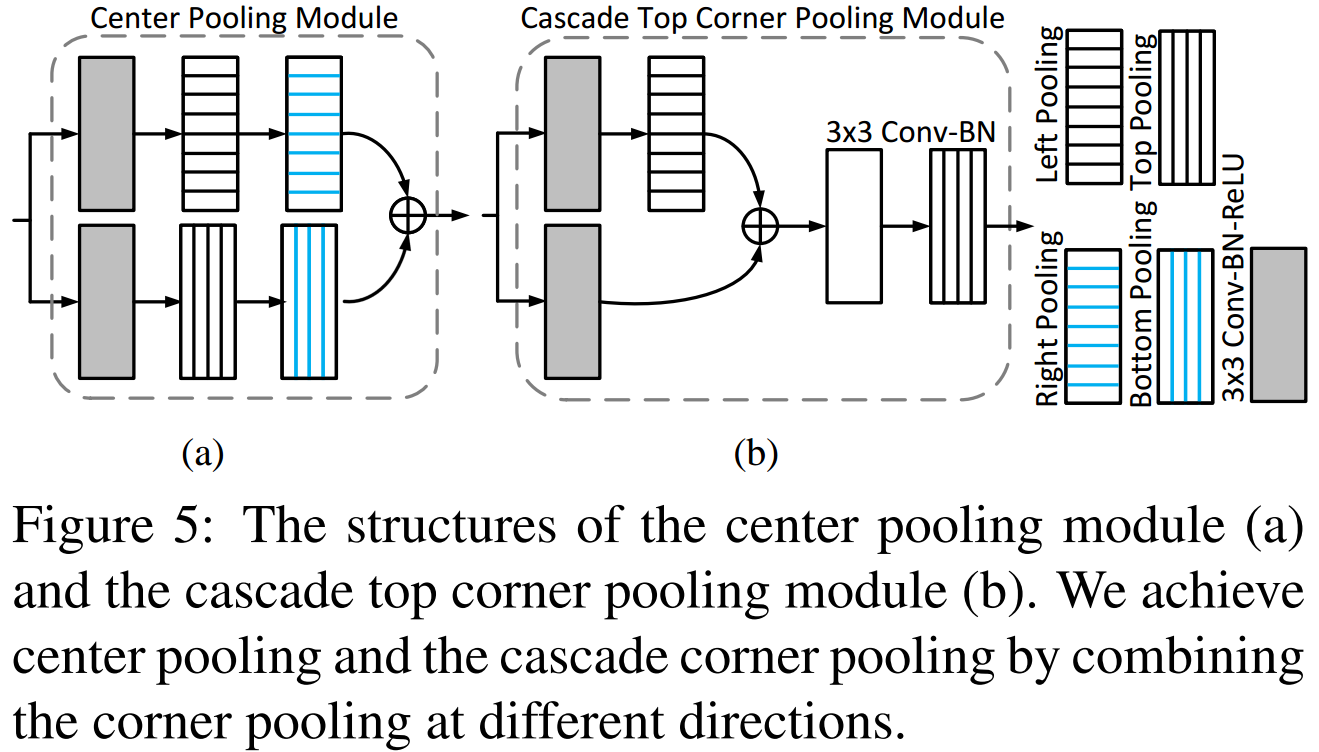　　如图 3.3 所示，这两个模块可通过不同方向的 corner pooling 组合而成，实现也较为简单。

3.2. Loss

　　相比 CornerNet，增加了 center Heatmaps 的 Loss 项，其它都一样： \[ L= L_{det}^{co} + L_{det}^{ce} + \alpha L_{pull}^{co} + \beta L_{push}^{co} + \gamma \left(L_{off}^{co}+L_{off}^{ce}\right) \tag{3.1}\]

4. ExtremeNet^[7]

　　如图 4.1 所示，ExtremeNet 继承了 CornerNet(CenterNet) 主干，所不同的是，ExtremeNet 预测了目标的上下左右四个点，这四个点都是在目标上的，而传统的目标框上的左上及右下点则离目标有一定距离。所以输出上，角点的 Heatmaps \(\in\mathbb{I}^{4\times C\times H\times W}\)，Center 点 Heatmaps \(\in\mathbb{I}^{C\times H\times W}\)，只对角点预测 Offsets \(\in\mathbb{R}^{4\times 2\times H\times W}\)，去掉了 Embedding 的预测。

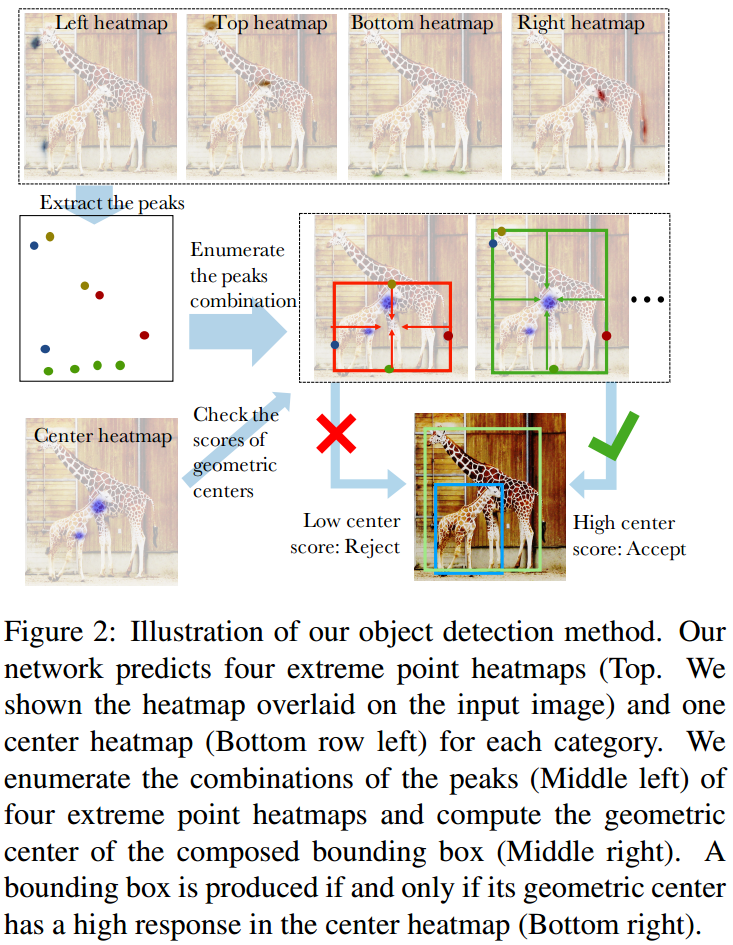　　CornerNet 与 CenterNet 因为预测的角点是目标框的左上及右下点，所以 Embedding 能较好的用于角点配对，而 ExtremeNet 预测的角点可能在目标框的任意位置，所以作者采用暴力穷举匹配的方法，实验表面效果也更好。如图 4.2 所示，最后判断是否是一个匹配到的角点，与 CenterNet 类似，也是判断待匹配角点的中心角点上是否有较强的 Center 响应。

5. CenterNet: Objects as Points^[8]

　　如图 5.1 所示，CenterNet 网络大体上还是继承了 CornerNet，在 2D 检测上，CenterNet 预测目标框的中心点 Center \(\in\mathbb{I}^{C\times H\times W}\)，中心点 Offsets \(\in\mathbb{R}^{2\times H\times W}\)，以及目标框的尺寸 size \(\in\mathbb{R}^{2\times C\times H\times W}\)。其 Loss 为： \[ L_{det}=L_k + \lambda_{size}L_{size}+\lambda_{off}L_{off} \tag{5.1} \] 　　Inference 的后处理只需要对 Center Heatmaps 作 3x3 的 max-pooling，不需要对目标框作 NMS！

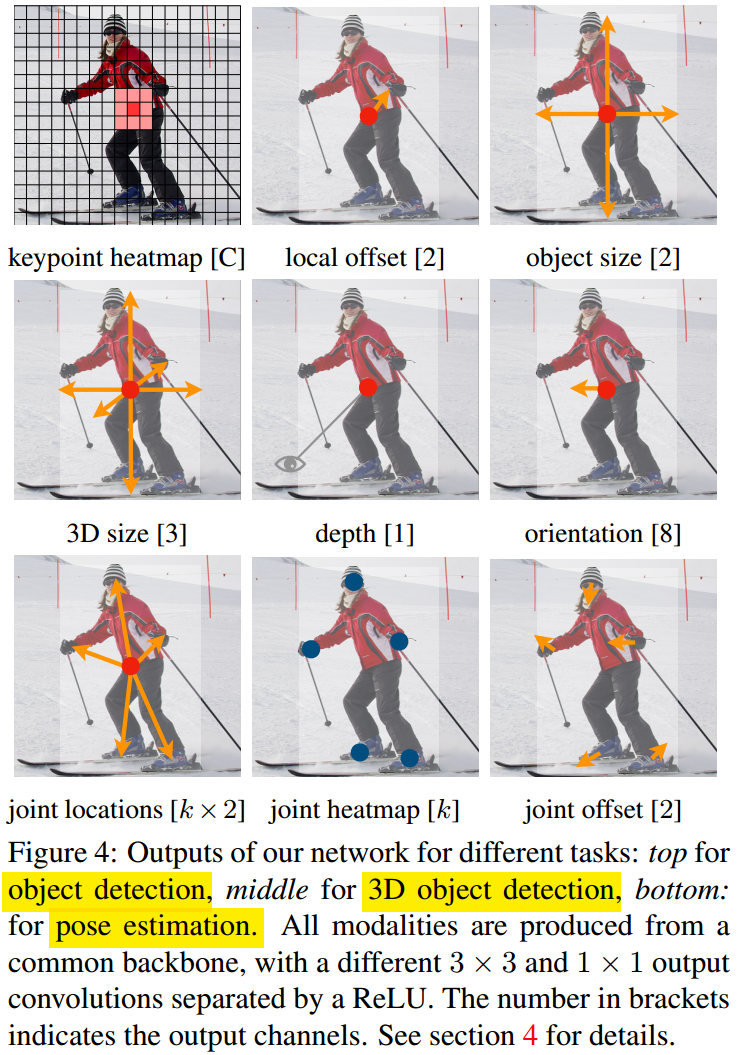　　此外，这种 pixel-level 的预测容易将其它任务也包含进来，如图 5.2 所示，作者还融入了 3D 检测，人体姿态估计。
　　3D 检测任务中，预测项为:

• 目标距离编码量 \(\sigma(\hat{d}_k)\in\mathrm{(0,1)}^{3\times C\times H\times W}\)，由于直接回归距离比较困难，实际距离的回归量为 \(\frac{1}{\sigma(\hat{d}_k)}-1\);
• 三围尺寸 \(\hat{\gamma}_k\in\mathbb{R}^{3\times C\times H\times W}\)，包括长，宽，高；
• 角度 \(\hat{\theta}_k\in\mathrm{[-\pi/2,\pi/2]}^{C\times H\times W}\)，直接回归比较困难，借鉴目前用的比较多的分类+回归的思想，设计编码量 \(\hat{\alpha}_k\in\mathbb{R}^{8\times C\times H\times W}\)，将角度划分为两个 bin，\(B_1=\left[-\frac{7\pi}{6},\frac{\pi}{6}\right]\)，\(B_2=\left[-\frac{\pi}{6},\frac{7\pi}{6}\right]\)，每个 bin 有四个预测量，其中两个预测量用来作 softmax 分类，另外两个预测量作相对于 bin 中心点 \(m_i\) 的 sin，cos 的 Offsets 量；

综上，3D 检测的 Loss 为： \[\left\{\begin{array}{l} L_{dep} = \frac{1}{N}\sum_{k=1}^N\left\vert\frac{1}{\sigma(\hat{d}_k)}-1-d_k\right\vert \\ L_{dim} = \frac{1}{N}\sum_{k=1}^N\left\vert\hat{\gamma}_k-\gamma_k\right\vert \\ L_{ori} = \frac{1}{N}\sum_{k=1}^N\sum_{i=1}^2\left(softmax\left(\hat{b}_i,c_i\right)+c_i\left\vert \hat{a}_i-a_i\right\vert\right) \end{array}\tag{5.2}\right.\] 其中 \(c_i=\mathbb{1}(\theta\in B_i)\)，\(a_i=\left(\mathrm{sin}(\theta-m_i),\mathrm{cos}(\theta-m_i)\right)\)，预测的角度可解码为 \(\hat{\theta}=arctan2\left(\hat{a}_{i1},\hat{a}_{i2}\right)+m_i\)。

6. FCOS^[9]

6.1. 网络结构

　　如图 6.1 所示，FCOS 提出了另一种目标框的表示方式，“参考点”+\((l,t,r,b)\)，当“参考点”是中心点时，就退化为中心点+尺寸的方式了。这种方式弱化了中心点的重要性，一定程度上“更有可能”回归出准确的目标框。 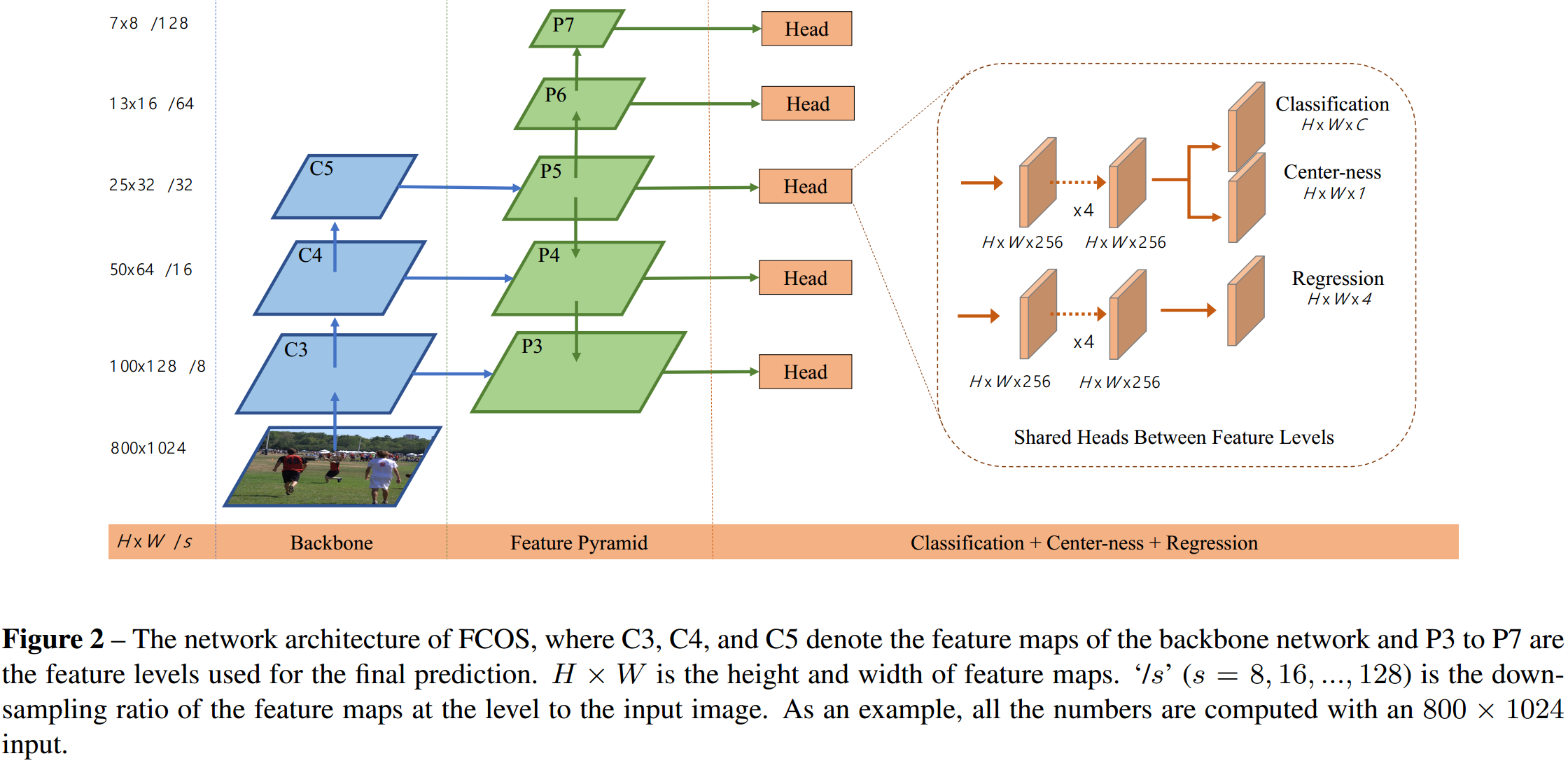　　如图 6.2 所示，FCOS 继承了 RetinaNet 主体网络，采用 FPN 形式，在不同尺度的特征层上进行目标检测。HourGlass 设计之初就是用于 pixel-level 的预测的，而 FPN 多尺度检测一定程度上更有利于框检测，不同尺度上检测不同大小的框能有效解决两个大小框中心点重合的情况，HourGlass 则无法解决，虽然这种情况很少。网络预测量有：

• Score Heatmaps \(\in\mathbb{R}^{C\times H\times W}\)，每个 Channel 的监督项是个二值图，代表了是否是该类别下的角点；
• Regression \(\in\mathbb{R}^{4\times H\times W}\)，“参考点” 上的 \((l,t,r,b)\)；
• Center-ness \(\in\mathbb{R}^{1\times H\times W}\)，监督“参考点”趋向于中心点，因为接近目标框边缘的“参考点”效果会比较差；

6.2. 多尺度检测

　　不同于 Hourglass 网络只在一个尺度上进行预测，FPN 在多尺度上对真值框的划分会比较复杂，基本准则是：不同尺度要检测不同尺寸的目标框，尺度越大(特征层越小)要检测的目标框尺寸越大。所以在真值框监督的划分上，具体的，如图 6.2 所示，多尺度特征表示为 \(\{P_i|i=3,4,5,6,7\}\)，对应每个特征层能回归的最大像素距离设定为 \(\{m_i|i=2,3,4,5,6,7\} = \{0,64,128,256,512,\infty\}\)。监督第 \(i\) 特征层学习的正样本真值框需满足： \[ m_{i-1}<\mathrm{max}(l^{gt},t^{gt},r^{gt},b^{gt})\le m_i \tag{6.1}\]

6.3. Loss

　　Loss 由三部分组成：

• 类别分类
  目标框内的所有点都作为正样本，所以直接采用 Focal Loss 中的 Loss 定义方式： \[ L_{det} = -\alpha(1-p_k)^\gamma\mathrm{log}(p_k) \tag{6.2}\]

• 目标框回归
  传统的 L2 Loss 用于目标框的直接回归有两个问题：

  1. 目标框参数只是作独立的优化；
  2. 较大的目标框有较大的 Loss；

这里采用 UnitBox 中提出的 IoU Loss^[13]： \[ L_{box} = -\mathrm{ln}(IoU_k) \tag{6.3} \]

• 参考点中心化监督
  不像 CornerNet 之流，这里的参考点全作为正样本，并没有向负样本方向的权重衰减，所以为了参考点趋向于中心点，作者提出了 Center-ness，其真值监督项为： \[ centerness^{gt} = \sqrt{\frac{\mathrm{min}(l^{gt},r^{gt})}{\mathrm{max}(l^{gt},r^{gt})} \times \frac{\mathrm{min}(t^{gt},b^{gt})}{\mathrm{max}(t^{gt},b^{gt})}} \tag{6.4} \] 从而可用 L1 Loss 来计算该项的 Loss。

7. FoveaBox^[10]

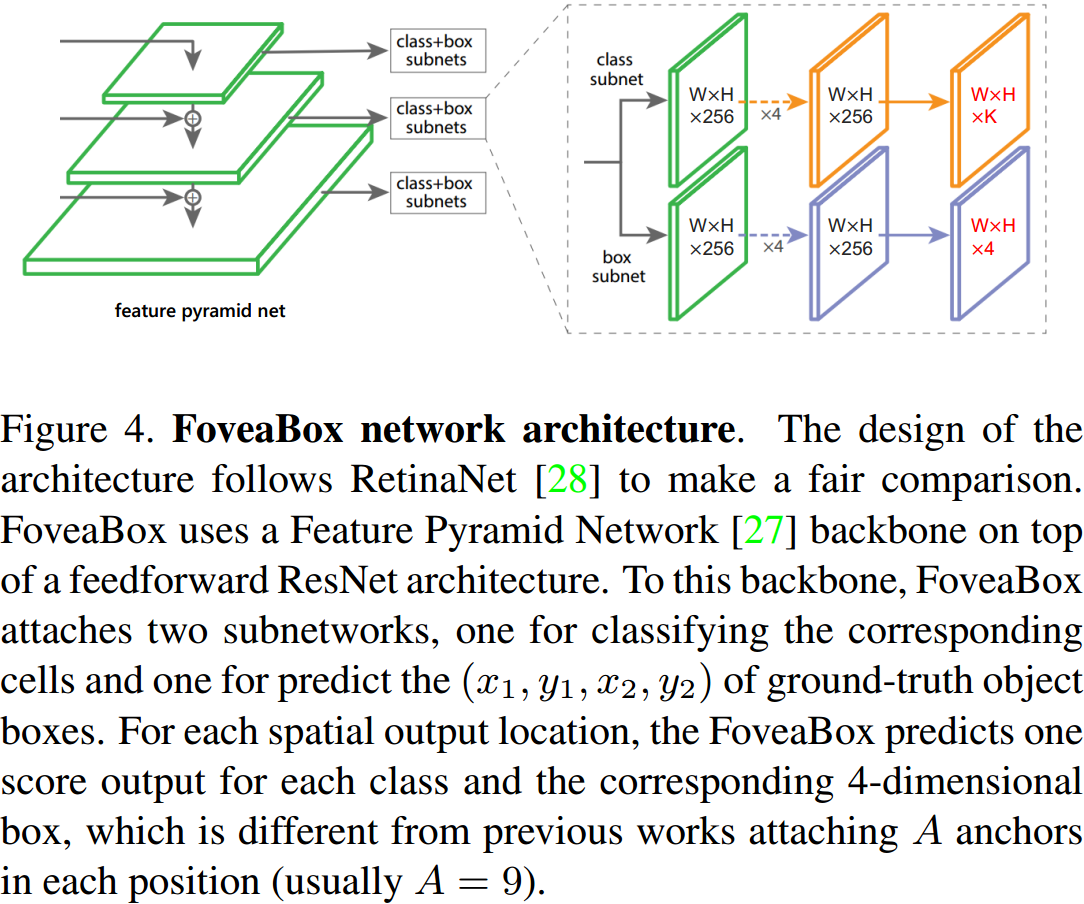　　如图所示，FoveaBox 完全继承了 RetinaNet 的主体网络，采用 FPN 形式。多尺度检测中的真值分配方式基本与 FCOS 一致，这里不做展开。 　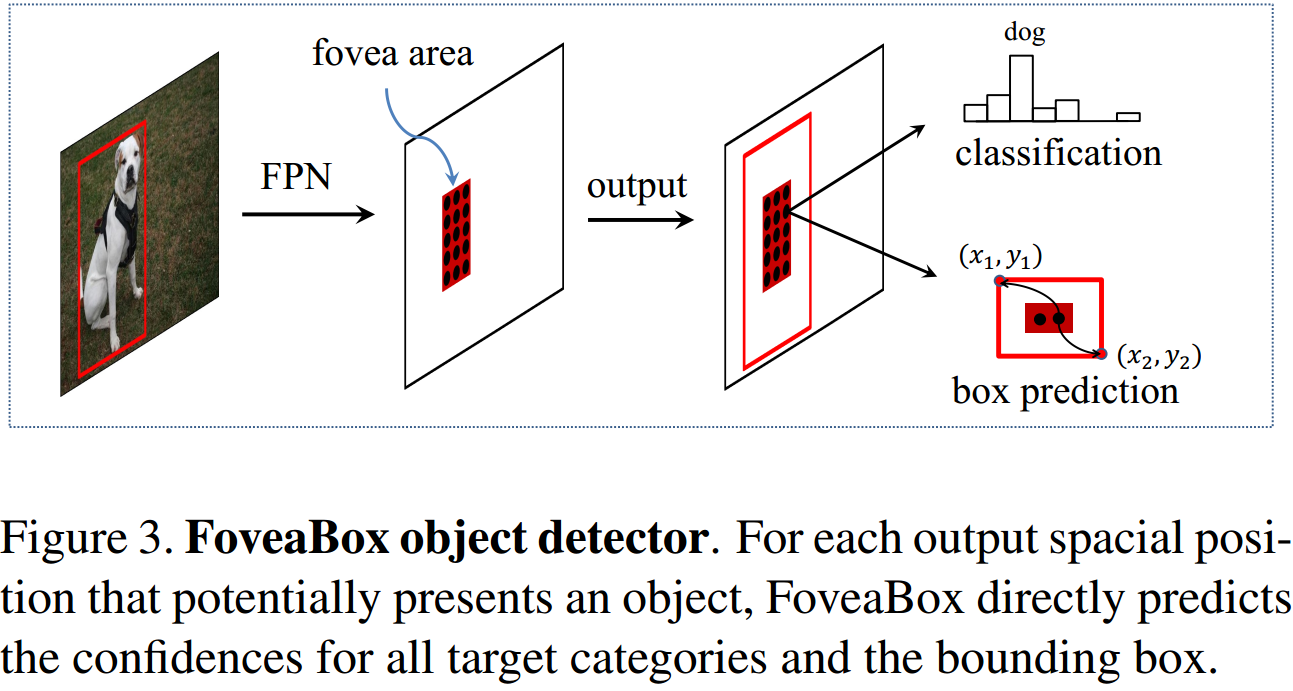　正负样本的分配上，作者提出了 Fovea 区域，如图 7.2 所示，目标框收缩一定比例后的区域定义为正样本，收缩一定比例后的区域外定义为负样本。
　　目标框的回归上，作者提出了另一种回归量，在 \((x,y)\) 像素点上，回归量定义为： \[\left\{\begin{array}{l} t_{x_1^{gt}} = \mathrm{log}\frac{2^l(x+0.5)-x_1^{gt}}{\sqrt{S_l}} \\ t_{y_1^{gt}} = \mathrm{log}\frac{2^l(y+0.5)-y_1^{gt}}{\sqrt{S_l}} \\ t_{x_2^{gt}} = \mathrm{log}\frac{x_2^{gt}-2^l(x+0.5)}{\sqrt{S_l}} \\ t_{y_2^{gt}} = \mathrm{log}\frac{y_1^{gt}-2^l(y+0.5)}{\sqrt{S_l}} \\ \end{array}\tag{7.1}\right.\] 其中 \(S_l\) 为第 \(l\) 特征层设计的最大检测像素长度的平方。

8. FSAF^[11]

　　网络结构及多尺度检测设置上与 FCOS，FoveaBox 并无新意。FSAF 新的东西是提出了多尺度特征层自动选择对应大小的真值目标框，用作本特征层的训练，具体选择的过程就是看每层特征层对该目标框输出的 Loss 大小，思想与 OHEM 或是 Focal Loss 差不多。该模块可与 Anchor-Based 方法一起嵌入到网络中。

9.参考文献

[1] Redmon, Joseph, et al. "You only look once: Unified, real-time object detection." Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.
[2] Huang, Lichao, et al. "Densebox: Unifying landmark localization with end to end object detection." arXiv preprint arXiv:1509.04874 (2015).
[3] Lin, Tsung-Yi, et al. "Focal loss for dense object detection." Proceedings of the IEEE international conference on computer vision. 2017.
[4] Law, Hei, and Jia Deng. "Cornernet: Detecting objects as paired keypoints." Proceedings of the European Conference on Computer Vision (ECCV). 2018.
[5] Law, Hei, et al. "CornerNet-Lite: Efficient Keypoint Based Object Detection." arXiv preprint arXiv:1904.08900 (2019).
[6] Duan, Kaiwen, et al. "Centernet: Keypoint triplets for object detection." Proceedings of the IEEE International Conference on Computer Vision. 2019.
[7] Zhou, Xingyi, Jiacheng Zhuo, and Philipp Krahenbuhl. "Bottom-up object detection by grouping extreme and center points." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019.
[8] Zhou, X., Wang, D., & Krähenbühl, P. (2019). Objects as Points arXiv preprint arXiv:1904.07850
[9] Tian, Zhi, et al. "FCOS: Fully Convolutional One-Stage Object Detection." arXiv preprint arXiv:1904.01355 (2019).
[10] Kong, Tao, et al. "FoveaBox: Beyond Anchor-based Object Detector." arXiv preprint arXiv:1904.03797 (2019).
[11] Zhu, Chenchen, Yihui He, and Marios Savvides. "Feature selective anchor-free module for single-shot object detection." arXiv preprint arXiv:1903.00621 (2019).
[12] Yang, Ze, et al. "RepPoints: Point Set Representation for Object Detection." arXiv preprint arXiv:1904.11490 (2019).
[13] Yu, Jiahui, et al. "Unitbox: An advanced object detection network." Proceedings of the 24th ACM international conference on Multimedia. ACM, 2016.
[14] Newell, Alejandro, Kaiyu Yang, and Jia Deng. "Stacked hourglass networks for human pose estimation." European conference on computer vision. Springer, Cham, 2016.
[15] Lin, Tsung-Yi, et al. "Feature pyramid networks for object detection." Proceedings of the IEEE conference on computer vision and pattern recognition. 2017.