准确的深度信息获取在自动驾驶中非常重要，所以激光点云以其稳定精确的深度测量优势在自动驾驶传感器配置中不可或缺。但是激光雷达昂贵而且获取的点云较为稀疏，由此可考虑两种替代方案：基于单目、双目的深度预测；以及基于单目，激光雷达的深度补全。
深度预测与深度补全都是为了获得稠密的图像像素级别深度信息，所以在自监督的损失函数上，非常相似。本文就提取归纳一些共同的优化点，并对各自的优化方向作阐述。
1. Self-supervised Depth Estimation
室外场景下，图像像素级别的深度信息真值很难获得，在位姿准确的情况下可累积激光点云的测量信息来填充大部分像素区域，以此作为真值；也可以借助 SLAM 建图定位技术，重建场景稠密的深度信息，从而使像素均能索引到真实的深度。但是以上两种方法都只能获得静态场景的深度信息。所以采用自监督的深度估计技术，就显得尤为重要。
本文介绍两篇文章：[1] 是基于图像的深度估计，[2] 是基于图像和激光雷达的深度补全。二者的网络结构都比较简单，主要是无监督/半监督的 Loss 设计。
1.1. Digging Into Self-Supervised Monocular Depth Estimation
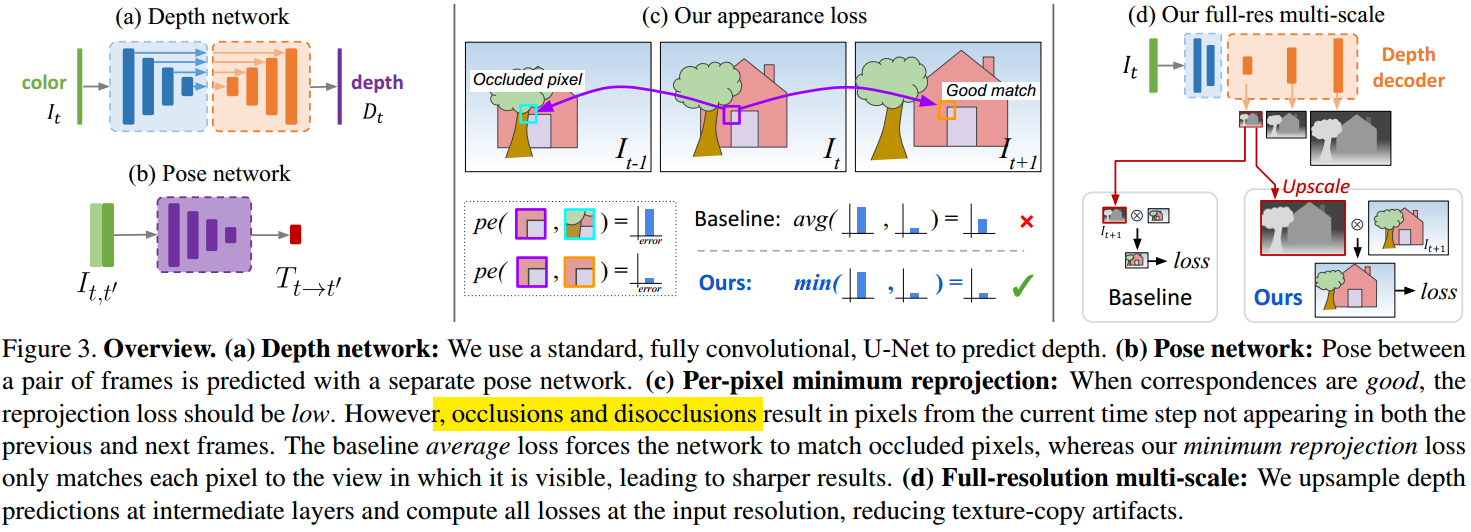如图 1. 所示，深度估计的网络输入为单帧，经过 Encoder-Decoder 输出像素级别的深度。Pose 估计的网络输入前后帧，输出前后帧的本体位姿变换。无监督 Loss 通过当前帧与前后帧的像素匹配计算，在遮挡或是非连续的情况下，当前帧的某些像素区域在前后帧中是不可见的(如图 2. 所示)，所以会产生较大的 Loss，本文提出了取最小化 Loss 的方法，有效解决该问题。此外，计算不同尺度下的 Loss。 
1.2. Self-Supervised Sparse-to-Dense: Self-Supervised Depth Completion from LiDAR and Monocular Camera
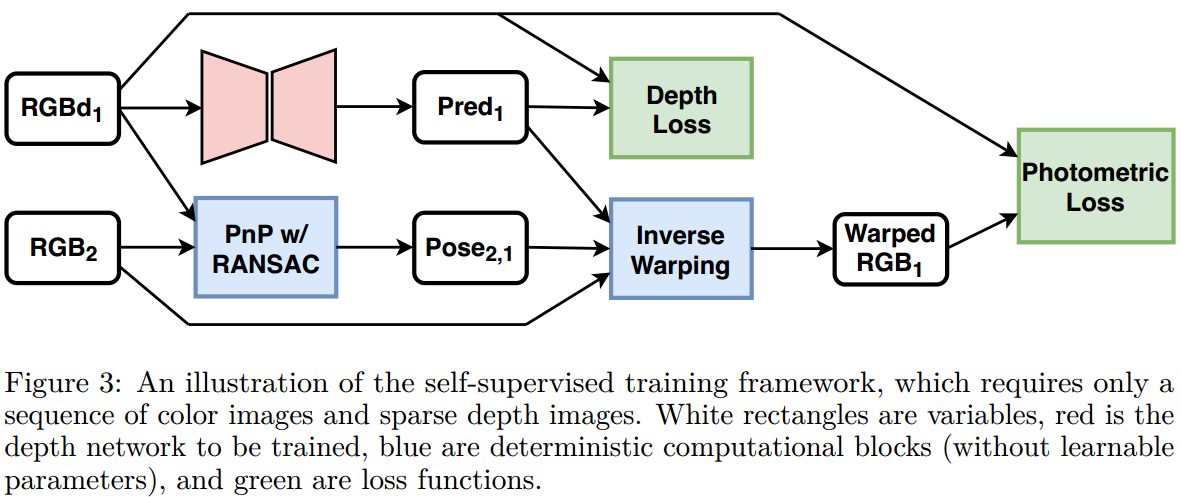如图 3. 所示，类似的，该方法输入为 RGB+Sparse LiDAR 数据，通过 Depth Loss 半监督，通过 Photometric Loss 无监督学习深度信息。其中 Pose 通过提取前后帧角点，匹配，然后求解 PnP 的方式计算得到。
2. Loss
无监督/半监督学习深度信息，Loss 的设计就很关键，以下列举几种常用的 Loss 设计方法。
2.1. Sparse Depth Loss
对于有对应的 LiDAR 点云的情况，可对点云打到的图像像素区域作有监督学习： \[\mathcal{L} _ {depth} = \Vert \mathbb{1} _ {\{d > 0\}}\cdot (\mathbf{pred-d})\Vert _ 2 ^ 2\tag{1}\]
2.2. Smoothness Loss
为了使得估计的深度信息在空间上较为平滑，[2] 采用简单的像素空间二次导数最小化的方法： \[\mathcal{L} _ {smooth} = \Vert\nabla ^ 2\mathbf{pred}\Vert _ 1\tag{2}\] [1] 则采用像素空间 Edge-aware 的平滑 Loss，这样在物理空间上深度信息没有拖影的现象： \[\mathcal{L} _ {smooth} = \vert\partial _ xd _ t ^ * \vert e ^ {-\vert \partial _ xI _ t\vert}+\vert\partial _ yd _ t ^ * \vert e ^ {-\vert \partial _ yI _ t\vert}\tag{3}\]
2.3. Photometric Reprojection Loss
设当前图像帧预测的深度信息为 \(\mathbf{pred} _ 0\)，相机内参矩阵为 \(\mathcal{K}\)，那么对于相机相对位姿为 \(T _ {0\rightarrow 1}\) 的图像 \(\mathbf{RGB} _ 1\)，其像素坐标系关系为：\(p _ 1=\mathcal{K}T _ {0\rightarrow 1}\mathbf{pred} _ 0(p _ 0)\mathcal{K} ^ {-1}p _ 0\)，由此可得到图像从 \(0\rightarrow 1\) 的变换： \[\mathbf{warped _ 1(p _ 0)}=\mathrm{bilinear}(\mathbf{RGB} _ 1(\mathcal{K}T _ {0\rightarrow 1}\mathbf{pred} _ 0(p _ 0)\mathcal{K} ^ {-1}p _ 0)) \tag{4}\] [2] 采用多尺度的 L1 Loss，并只在无激光点云的像素区域作无监督学习： \[\mathcal{L} _ {photometric}(\mathbf{warped _ 1,RGB _ 1})=\sum _ {s\in S} \frac{1}{s}\left\Vert\mathbb{1} ^ {(s)} _ {d==0}\cdot(\mathbf{warped _ 1} ^ {(s)}-\mathbf{RGB _ 1} ^ {(s)})\right\Vert _ 1 \tag{5}\] [1] 采用 L1 与 SSIM[3] 的方式来构造 Photometric 损失函数： \[\mathcal{L} _ {photometric}(\mathbf{warped _ 1,RGB _ 1}) = \frac{\alpha}{2}(1-\mathrm{SSIM}(\mathbf{warped _ 1,RGB _ 1}))+(1-\alpha)\Vert\mathbf{warped _ 1-RGB _ 1}\Vert _ 1\tag{6}\] 其中 SSIM 是描述图像结构信息相似度的函数。此外 [1] 除了多尺度训练外，还作了两点改进：
Per-Pixel Minimum Reprojection
如图 2. 所示，在遮挡以及图像边缘情况，\(\mathbf{warped} _ 1\) 可能在 \(\mathbf{RGB} _ 1\) 上找不到对应的像素点，导致损失函数失真变大，所以引入 \(\mathbf{RGB} _ {-1}\)，同时考虑 \(\mathbf{warped} _ {-1}\) 与其匹配: \[\mathbf{warped _ {-1}(p _ 0)}=\mathrm{bilinear}(\mathbf{RGB} _ {-1}(\mathcal{K}T _ {0\rightarrow -1}\mathbf{pred} _ 0(p _ 0)\mathcal{K} ^ {-1}p _ 0)) \tag{7}\] 取二者最小的误差作为投影误差： \[\mathcal{L} _ {photometric} = \sum _ p \mathop{\min}\limits \{pe _ {-1}, pe _ {1}\} \tag{8}\] 其中 \(pe\) 是像素级别的 SSIM 与 L1 误差。Auto-Masking Stationary Pixels
对于静态场景以及运动物体，投影误差来描述深度估计都是不准确的，所以用一个像素级别的 mask 来计算最终的损失函数，判断一个像素是否计入损失函数的条件为 \(\mathbf{warped}\) 像素值与目标像素值的误差是否小于原始像素值与目标像素值的误差： \[\mu = \left[ \mathop{\min}\limits \{pe _ {-1} ^ {warped}, pe _ {1} ^ {warped}\} <\mathop{\min}\limits \{pe _ {-1} ^ {unwarped}, pe _ {1} ^ {unwarped}\} \right] \tag{9}\] 其中 \([\cdot]\) 使得 \(\mu\in \{0,1\}\)。这样就能在静态场景以及运动物体与本车速度相似的情况下，不计入该区域的投影损失误差值。
3. Reference
[1] Godard, Clément, et al. "Digging into self-supervised monocular depth estimation." Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019.
[2] Ma, Fangchang, Guilherme Venturelli Cavalheiro, and Sertac Karaman. "Self-supervised sparse-to-dense: Self-supervised depth completion from lidar and monocular camera." 2019 International Conference on Robotics and Automation (ICRA). IEEE, 2019.
[3] Wang, Zhou, et al. "Image quality assessment: from error visibility to structural similarity." IEEE transactions on image processing 13.4 (2004): 600-612.
