Heteroscedastic Aleatoric Uncertainty 中详细讨论了 Aleatoric Uncertainty 的建模以及应用。本文讨论 Epistemic Uncertainty 的建模，以及在 Active Learning 中的应用。Epistemic Uncertainty 描述了模型因为缺少训练数据而存在的不确定性，所以其可应用于 Active Learning。应用场景有：
- 减少训练时间：在大数据集下，训练时挑选当前模型认知困难的样本，减少训练数据从而减少训练时间；
- 减少无效标注：只挑选当前模型认知困难的样本进行标注、迭代模型；
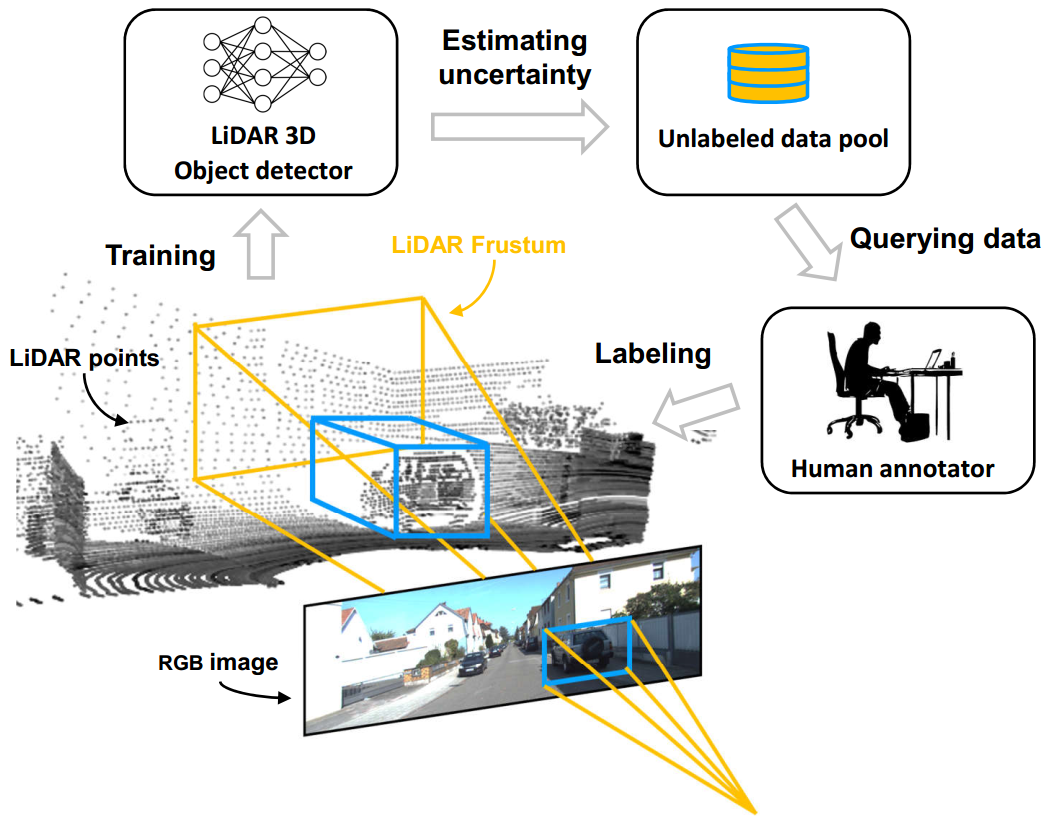[1]中提到的一种 Active Learning 工作流如图 1. 所示，重要环节有 Estimating Uncertainty 以及 Querying Data。该工作流假设了一个完美的图像检测器(至少有个完美的召回率)，图像检测器提供目标 proposal，3D 检测对 proposal 作 uncertainty 估计，从而确定是否标注。 Estimating Uncertainty 指的是 Epistemic Uncertainty 的建模；Querying Data 则设计一种策略，其能通过估计的 Uncertainty 来选择模型认知困难的样本。
由于 Epistemic Uncertainty 只能通过 Monte-Carlo 等方法近似得到，这些方法都是基于模型预测的目标进行 Uncertainty 估计的，所以对于漏检的目标，其 Uncertainty 是无法有效获取的。换句话说，本文讨论的 Epistemic Uncertainty 只能抓取预测的正样本(TP)置信度不高，以及误检(FP)的 Uncertainty 信息，无法获得TP置信度非常低的样本 Uncertainty，即完全没见过的目标。所以基于 Epistemic Uncertainty 的 Active Learning，理论上只能使正样本置信度提高，以及消除误检；对于漏检，需要加入一定的随机性，让模型先“见到”这种类型的目标。
1. Estimating Epistemic Uncertainty
针对一批训练数据集\(\{\mathbf{X,Y}\}\)，训练模型 \(\mathbf{y=f^W(x)}\)，在贝叶斯框架下，预测量的后验分布为[3]： \[p\left(\mathbf{y\vert x,X,Y}\right) = \int p\left(\mathbf{y\,|\,f^W(x)}\right) p\left(\mathbf{W\,|\,X,Y}\right)d\mathbf{W} \tag{1}\] 其中 \(p(\mathbf{W\,|\,X,Y})\) 为模型参数的后验分布，描述了模型的不确定性，即 Epistemic Uncertainty；\(p\left(\mathbf{y\,|\,f^W(x)}\right)\) 为观测似然，描述了观测不确定性，即Aleatoric Uncertainty。接下来讨论如何计算 Epistemic Uncertainty。
1.1. 分类问题
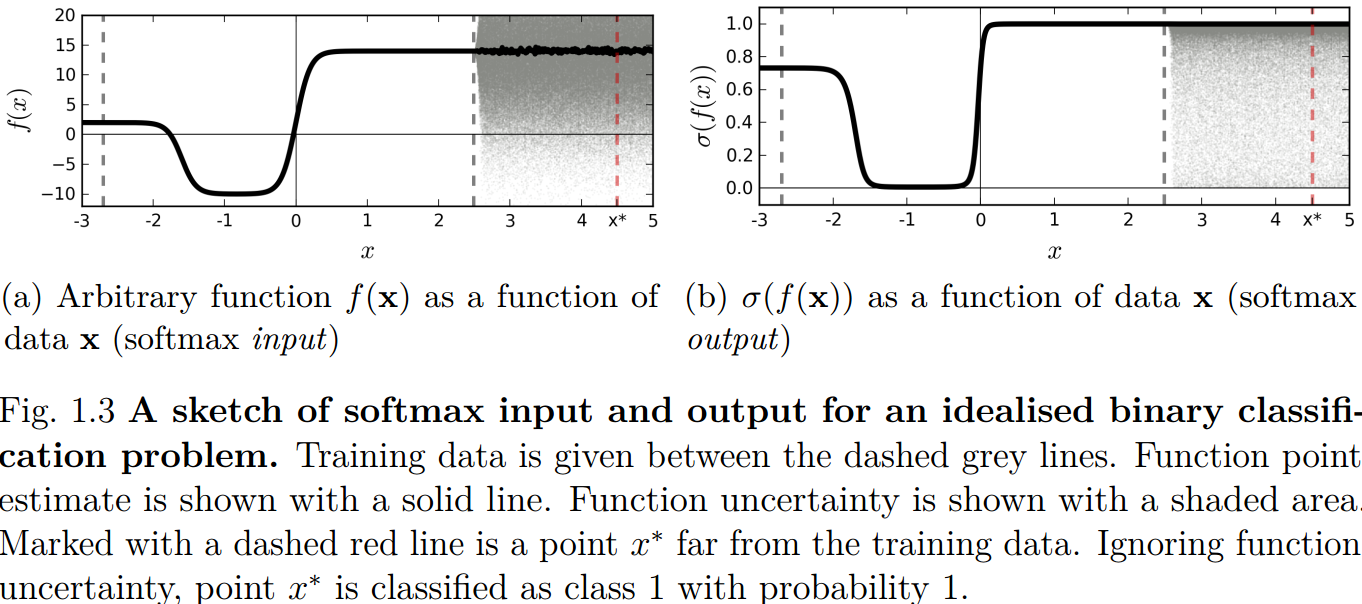如图 2. 所示[2]，softmax 可能会对没见过的目标产生较高的概率输出(如误检)。所以不能直接使用分类的概率输出作为 Uncertainty 估计。
- Monte-Carlo Dropout
[2]中提出了 Monte-Carlo 近似求解 Epistemic Uncertainty 的方法，其指出：在训练阶段，Dropout 等价于优化网络权重 \(W\) 的 Bernoulli 分布；在测试阶段，使用 Dropout 对样本进行多次测试，能得到模型权重的后验分布，即 Epistemic Uncertainty。由此得到： \[p(\mathbf{y|x}) \approx \frac{1}{T}\sum^T_{t=1} p(\mathbf{y|x,W}_t) = \frac{1}{T}\sum^T_{t=1}softmax_{(\mathbf{W}_t)}(\mathbf{x}) \tag{2}\] 其中 \(\mathbf{W}_t\) 为第 \(t\) 次 Inference 网络权重。 - Deep Ensembles
Deep Ensemble 则是一种非贝叶斯的方法，该方法用不同的初始化方法训练一系列网络 \(\{\mathbf{M} _ e\} _ {e=1}^E\)。那么： \[p(\mathbf{y|x}) \approx \frac{1}{E}\sum^E_{e=1} p(\mathbf{y|x,M}_e) = \frac{1}{E}\sum^E_{e=1}softmax_{(\mathbf{M}_e)}(\mathbf{x}) \tag{3}\]
有了预测的概率后，可用 Shannon Entropy 或者 Mutual Information 来计算目标的信息量，即 Uncertainty。
- Shannon Entropy(SE)
SE 计算公式为: \[\mathcal{H}[\mathbf{y|x}] = -\sum^C_{c=1}p(y=c|\mathbf{x})\,\mathrm{log}\,p(y=c|\mathbf{x}) \tag{4}\] - Mutual Information(MI)
由于 Monte-Carlo 以及 Deep Ensembles 获取的是概率分布，以 Monte-Carlo 为例，由此可计算 MI： \[\mathcal{I}[\mathbf{y;W}] = \mathcal{H}[\mathbf{y|x}] - \mathbb{E}\mathcal{H}[\mathbf{y|x,W}] \approx \mathcal{H}[\mathbf{y|x}] + \frac{1}{T}\sum_{t=1}^T\sum_{c=1}^Cp(y=c|\mathbf{x,W}_t)\,\mathrm{log}\,p(y=c|\mathbf{x,W}_t) \tag{5}\]
SE 测量的是预测 Uncertainty，MI 测量的是模型对该数据的 Uncertainty。根据该 Uncertainty，即可挑选样本进行标注。Uncertainty 越高，代表该样本对模型的信息量更大，所以需要进一步标注来训练模型。
1.2. 回归问题
Monte-Carlo 采样下，假设获得的回归量为 \(\{\mathbf{v}\}_{t=1}^T\)。那么其均值和方差为： \[\left\{\begin{array}{l} \mathcal{M}_{\mathbf{v}} \approx \frac{1}{T}\sum_{t=1}^T\mathbf{v}_t \\ \mathcal{C}_{\mathbf{v}} = \frac{1}{T}\sum_{t=1}^T\mathbf{v}_t\mathbf{v}_t^T-\mathcal{M}_{\mathbf{v}}\mathcal{M}_{\mathbf{v}}^T \end{array}\tag{6}\right.\] 由此得到回归量的 Uncertainty： \[TV_{\mathbf{v}} = trace\left(\mathcal{C}_{\mathbf{v}} \right) \tag{7}\] 该 Uncertainty 越大，说明该数据对模型的信息也越多，所以可进一步标注训练。
2. Metrics
TODO
3. Reference
[1] Feng, Di, et al. "Deep active learning for efficient training of a lidar 3d object detector." arXiv preprint arXiv:1901.10609 (2019).
[2] Gal, Yarin. Uncertainty in deep learning. Diss. PhD thesis, University of Cambridge, 2016.
[3] Feng, Di, Lars Rosenbaum, and Klaus Dietmayer. "Towards safe autonomous driving: Capture uncertainty in the deep neural network for lidar 3d vehicle detection." 2018 21st International Conference on Intelligent Transportation Systems (ITSC). IEEE, 2018.
