文章 pruning 中详细阐述了模型压缩中 Pruning 的基本方法与理论。Pruning 可分为 Structured Pruning 与 Unstructured Pruning 两种，由于 Structured Pruning 不需要特定的芯片支持，可直接在现有 CPU/GPU 架构下进行加速，所以值得作研究及应用。而 Structured Pruning 主要指 Filter Pruning，以及伴随的 Channel Pruning。本文对近期 Filter Pruning 的进展作一个阐述及思考。
[1] 得出结论：Pruning 的本质并不应该是选择重要的 filter/channel，而应该是确定 filter/channel 的数量，在此基础上，从零开始训练也能达到原来的性能。所以 Pruning 其实只是 AutoML/NAS 领域的一个子任务，即用 AutoML/NAS 是能解决 Pruning 问题的，但是 AutoML/NAS 方法又相对复杂且耗时，所以短期内可能传统的预定义剪枝方法更容易得到应用。本文从预定义剪枝方法和自动学习剪枝方法两大块来作归纳思考。
1. 问题描述
假设预训练好的网络 \(F\)，其有 \(L\) 层卷积，所有卷积层的 Filter 表示为： \[ W=\{W^i\} _ {i=1}^L= \left\{\{W^i_j\} _ {j=1}^{c_i}\in\mathbb{R}^{d_i\times c_i}\right\} _ {i=1}^L \tag{1} \] 其中 \(d_i=c_{i-1}\times h_i\times w_i\)；\(c_i,h_i,w_i\) 分别是第 \(i\) 层卷积的 filter 数量，高，宽；\(W_j^i\) 是第 \(i\) 层卷积第 \(j\) 个 filter。
目标是搜索被剪枝的网络 \(\mathcal{F}\)，剪枝后的 Filter 表示为： \[ \mathcal{W}=\{\mathcal{W}^i\} _ {i=1}^L= \left\{\{\mathcal{W}^i_j\} _ {j=1}^{\tilde{c}_i}\in\mathbb{R}^{d_i\times \tilde{c} _ i}\right\} _ {i=1}^L \tag{2} \] 其中 \(\tilde{c} _ i=\lfloor p_i\cdot c_i\rceil\)，\(p_i\) 为 Pruning Rate。
Filter Pruning 会导致输出的特征 Channel 数减少，对应的下一层的每个 Filter 参数需要相应的裁剪，如 pruning 中提到的三种结构下的 Pruning，尤其需要注意后两种有交点的结构，剪枝时需要作一定的约束(为了简单，交点对应的 Filter 可以选择不剪枝)。
2. 预定义剪枝方法
预定义剪枝网络方法通常预定义的是 \(P=\{p_i\} _ {i=1}^L\)，其剪枝步骤为：
- Training
根据任务训练网络； - Pruning
设计 Filter 重要性度量准则，然后根据预定义的剪枝率，进行 Filter 剪枝； - Fine-tuning
对剪枝好的网络，进行再训练；
2.1. Soft Filter Pruning[2][12]
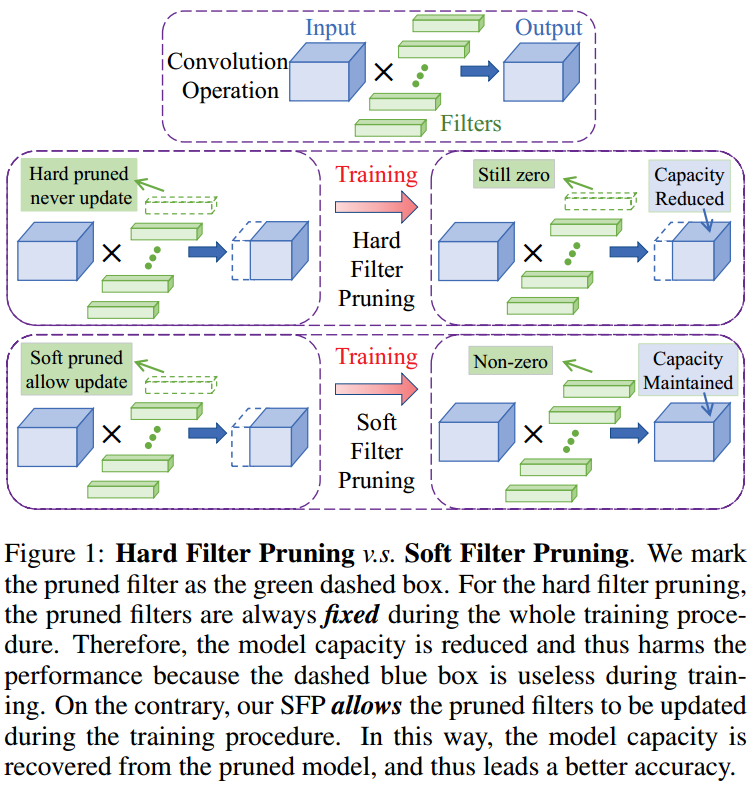如图 1. 所示，其核心思想就是剪枝后的 Filter 在 Fine-tuning 阶段还是保持更新，由此 Pruning，Fine-tuning 迭代获得较优剪枝结果。Filter 重要性度量准则为： \[\left\Vert W_j^i\right\Vert _ p = \sqrt[p]{\sum_{cc=0}^{c_{i-1}-1}\sum_{k_1=0}^{h_i-1}\sum_{k_2=0}^{w_i-1}\left\vert W_j^i(cc,k_1,k_2)\right\vert ^p} \tag{3}\]
2.2. Filter Sketch[3][13]
选择 Filter 进行剪枝，另一种思路是，如何选择一部分 Filter，使得该 Filter 集合的信息量与原 Filter 集合信息量近似: \[\Sigma_{W^i}\approx \Sigma_{\mathcal{W}^i} \tag{4}\] 这里的信息量表达方式采用了协方差矩阵: \[\begin{align}
\Sigma_{W^i} &= \left(W^i-\bar{W}^i \right)\left(W^i-\bar{W}^i \right)^T \\
\Sigma_{\mathcal{W}^i} &= \left(\mathcal{W}^i-\mathcal{\bar{W}}^i \right)\left(\mathcal{W}^i-\mathcal{\bar{W}}^i \right)^T \\
\end{align} \tag{5}\] 其中 Filter 权重符合高斯分布，即 \(\bar{W}^i=\frac{1}{c_i}\sum _ {j=1}^{c _ i}W _ j ^ i\approx 0\)，\(\mathcal{\bar{W}} ^ i=\frac{1}{\tilde{c} _ i}\sum _ {j=1}^{\tilde{c} _ i}\mathcal{W} _ j^i\approx 0\)。由式(4)(5)，构建最小化目标函数： \[\mathop{\arg\min}\limits_{\mathcal{W}^i}\left\Vert W^i(W^i)^T-\mathcal{W}^i(\mathcal{W}^i)^T \right\Vert \tag{6}\] 将该问题转换为求取 \(W^i\) 矩阵的 Sketch 问题，则： \[\left\Vert W^i(W^i)^T-\mathcal{W}^i(\mathcal{W}^i)^T \right\Vert _F \leq \epsilon\left\Vert W^i\right\Vert^2_F \tag{7}\] 
式(7)可用图 2. 所示的算法求解，最终的 Pruning 算法过程如图 3. 所示，改进的地方主要是 Filter 选择的部分，采用了 Matrix Sketch 算法。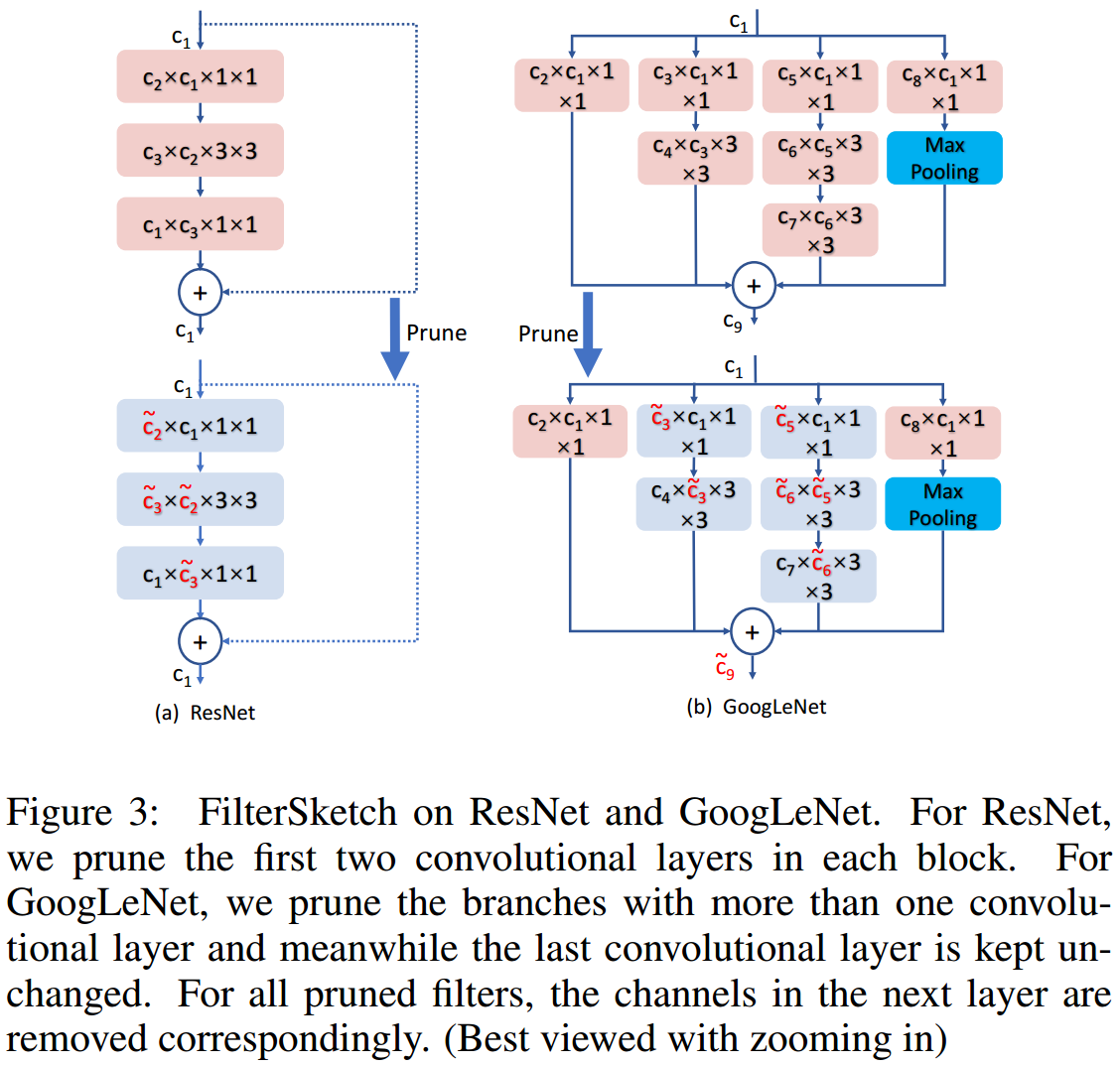 
pruning 中提到有分支结构的裁剪会比较麻烦，所以如图 4. 所示，本方法对分支节点的 Filter 不做裁剪处理，简化了问题。
2.3. Filter Pruning via Geometric Median[4][14]
在预定义剪枝网络方法的三个步骤中，大家普遍研究步骤二中 Filter 的重要性度量设计。Filter 重要性度量基本是 Smaller-norm-less-informative 思想，[5] 中则验证了该思想并不一定正确。Smaller-norm-less-informative 假设成立的条件是：
- Filter 权重的规范偏差(norm deviation)要大；
- Filter 权重的最小规范要小；
只有满足这两个条件，该假设才成立，即可以裁剪掉规范数较小的 Filter。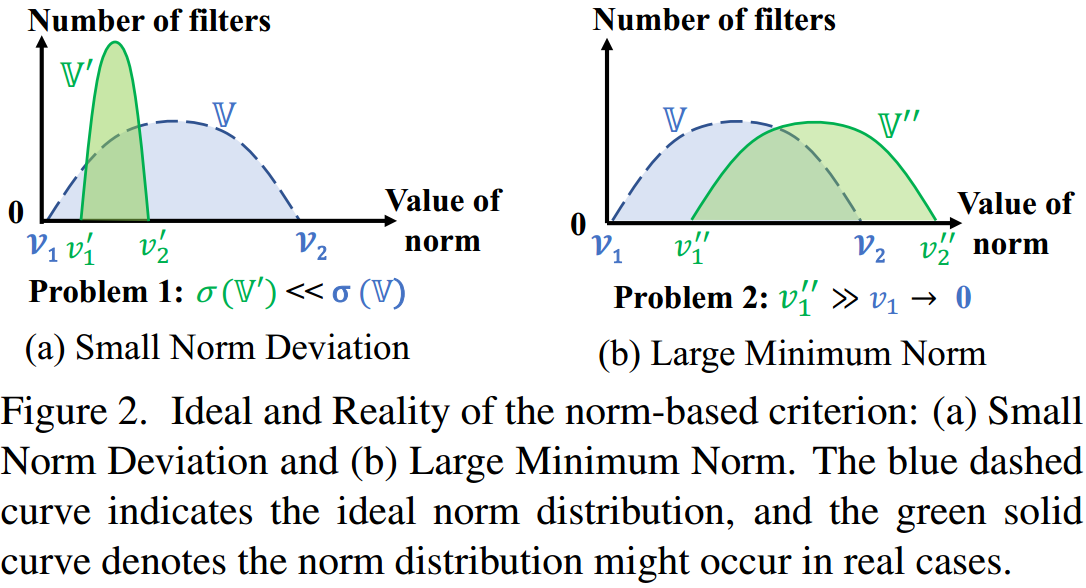 
但是，如图 5. 所示，实际 Filter 的权重分布和理想的并不一致，当 Filter 分布是绿色区域时，采用 Smaller-norm-less-informative 就不合理了，而这种情况还比较多。一般性的，前几层网络的权重规范数偏差会比较大，后几层则比较小。
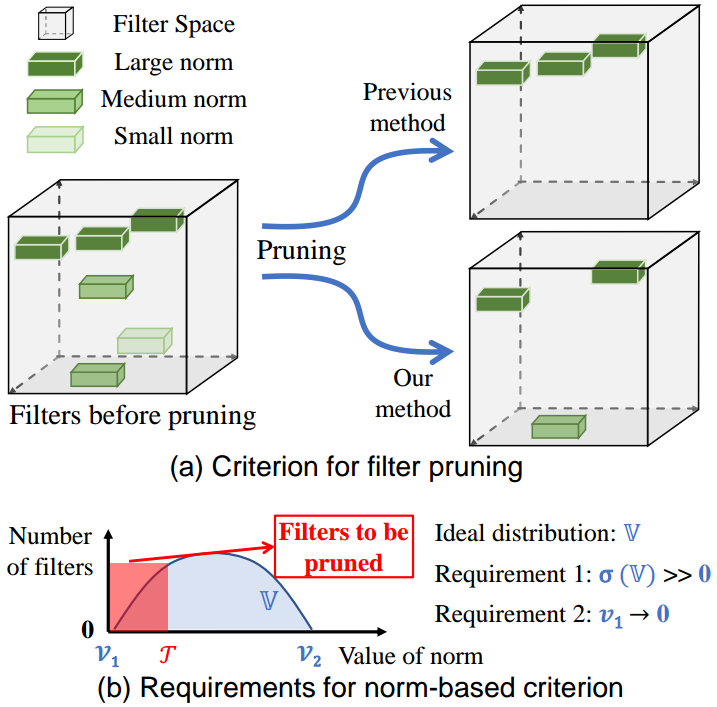由此，本方法提出一种基于 Geometric Median 的 Filter 选择方法，如图 6. 所示，基于 Smaller-norm-less-informative 的裁剪后留下的均是规范数较大的 Filter，这还存在一定的冗余性，本方法则通过物理距离测算，剪掉冗余的 Filter。另一个角度可理解为最大程度的保留 Filter 集合的大概及具体信息，其思想与 FilterSketch 类似。
根据 Geometric Median 思想，第 \(i\) 层卷积要裁剪掉的 Filter 为： \[W^i_{j^\ast}=\mathop{\arg\min}\limits_{W^i_{j^\ast}\,|\,j^\ast\in[0,c_i-1]}\sum_{j'=0}^{c_i-1}\left\Vert W^i_{j^\ast}-W^i_{j'}\right\Vert_2 \tag{8}\] 由此裁剪掉满足条件的 \(W _ {j^*}^i\)，直至符合裁剪比率。本方法的思想非常类似于 Farthest Point Sampling 采样，留下的 Filter 即为原 Filter 集合采样的结果，且最大程度的保留了集合的信息。
3. 自动学习剪枝方法
3.1. ABCPruner[6][16]
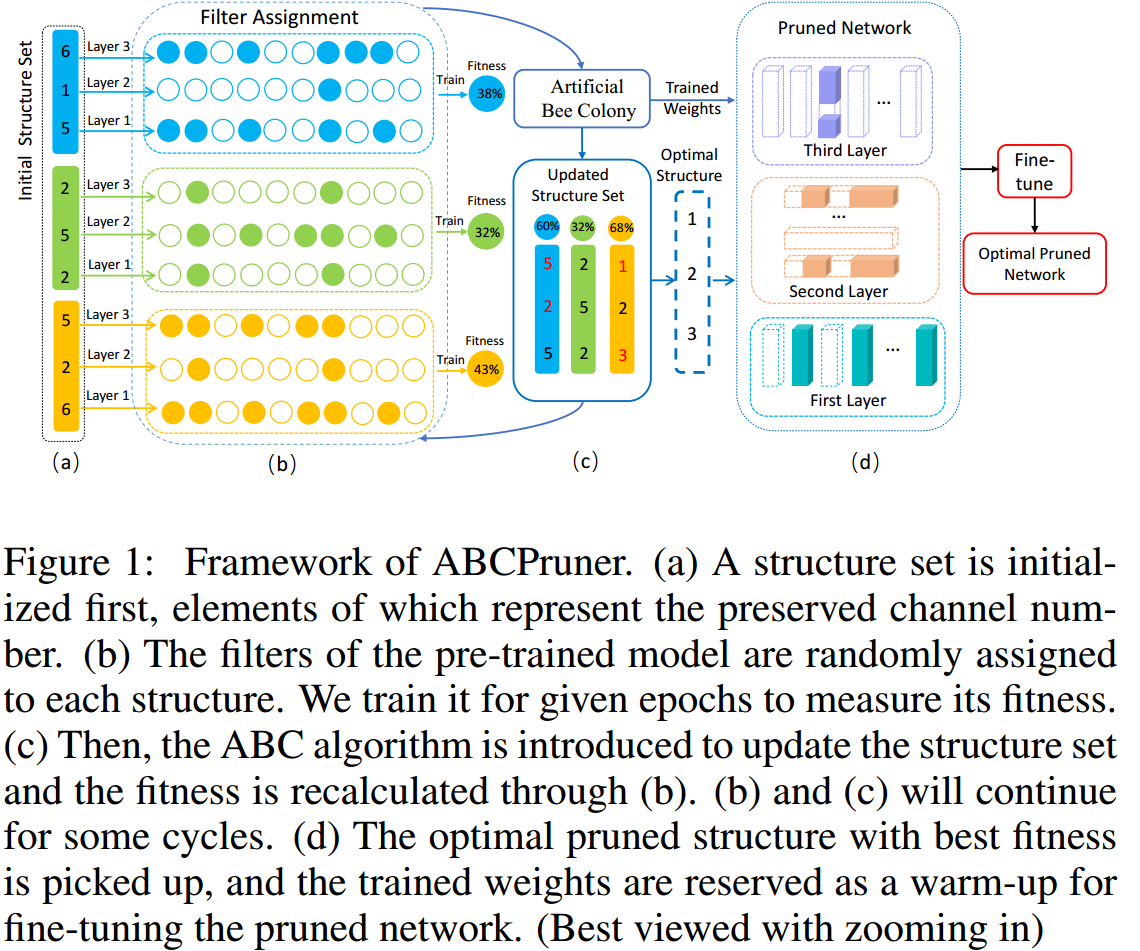出于[1]的结论：剪枝的本质应该是直接找到每层卷积最优的 Filter 数量，在此基础上从零开始训练也能达到原来的性能。ABCPruner 的目标就是搜索每层最优的 Filter 数量，如图 7. 所示，ABCPruner 步骤为：
- 初始化一系列不同 Filter 数量的网络结构；
- 每个网络结构从 pre-trained 网络中继承权重值，fine-tune 获得每个网络的 fitness(即 accuracy)；
- 用 ABC 算法更新网络结构；
- 重复迭代 2,3 步骤，获取最高的 fitness 网络作为最终网络结构；
3.2. MetaPruning[7][17]
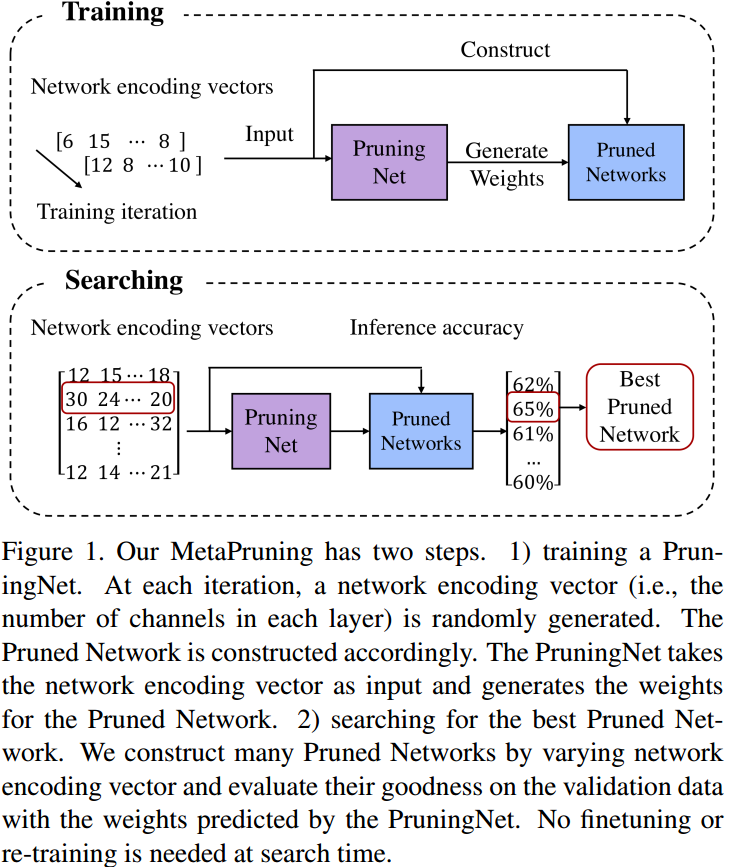同样，本方法也是基于[1]的结论。这里设计 PruningNet 来控制裁剪，步骤为：
- Training PruningNet
PruningNet 输入为网络编码向量，即每层卷积的 Filter 数量，输出为产生网络权重的编码量，如 size reshape，crop。每次训练时随机生成网络编码量，网络编码量与 PruningNet 输出共同决定了 PrunedNet 权重，两个网络联合训练； - Searching for the Best Pruned Net
即 Inference 过程，寻找最优的网络编码量，使得 PrunedNet 精度最高；得到最优网络后，不需要 fine-tuning。
3.3. Generative Adversarial Learning[8]
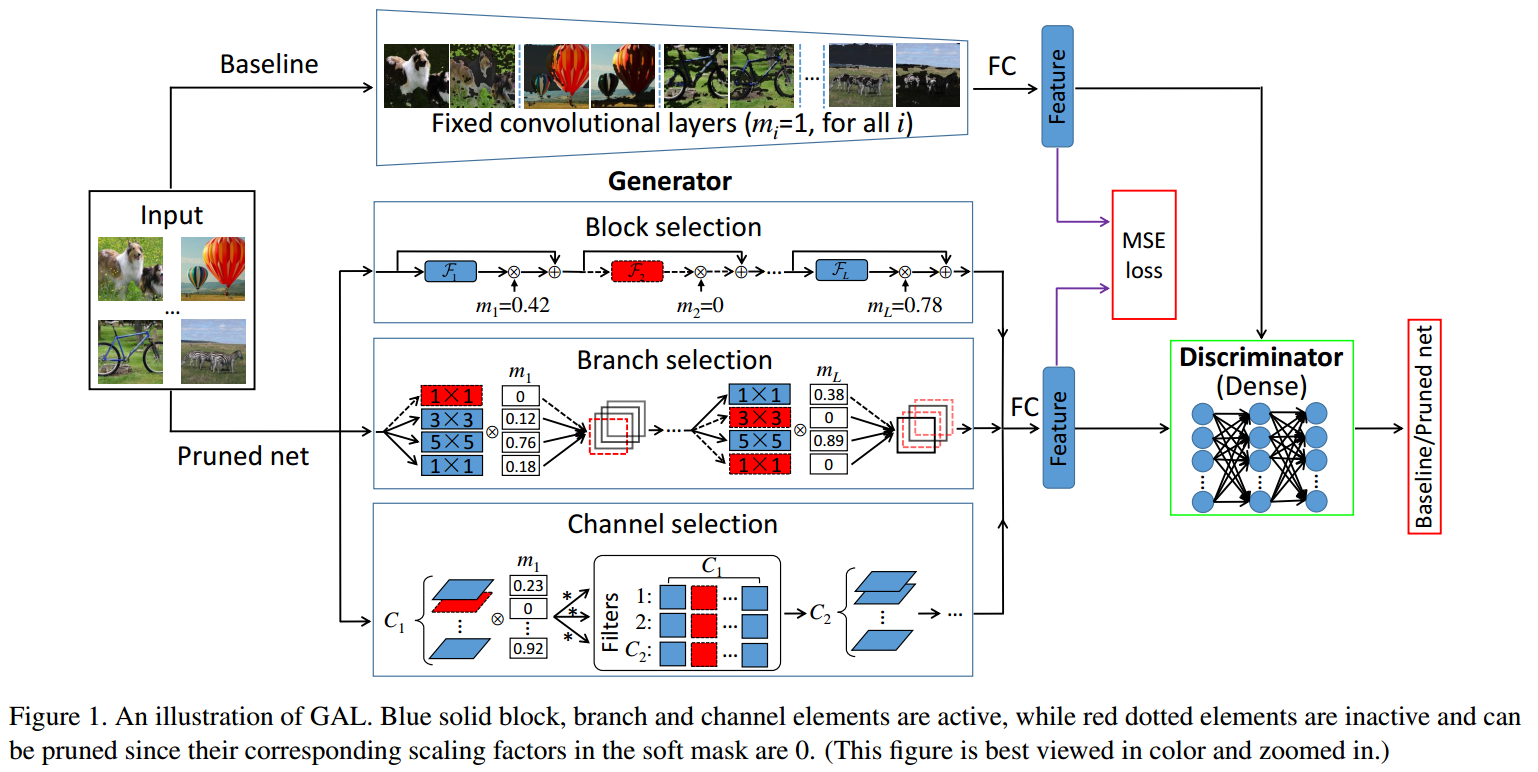本方法主要思想来自知识蒸馏(Knowledge Distillation)和生成对抗网络(Generative Adversarial Network)，如图 9. 所示，Baseline 为完整的原始网络，PrunedNet 是为了学习一个 soft mask 来动态选择 block，branch，channel，最终裁剪后的网络由 soft mask 决定。
从知识蒸馏的角度：Baseline 就是一个大容量的教师网络，Pruned Net 就是个小容量的学生网络，用大容量网络来监督小容量网络学习。从生成对抗学习的角度：Baseline 是原始网络，PrunedNet 是生成的对抗网络，用一个 Discriminator 网络来区分原始网络与生成的对抗网络的区别，使生成的对抗网络输出逼近于原始网络。
4. Reference
[1] Liu, Zhuang, et al. "Rethinking the Value of Network Pruning." International Conference on Learning Representations. 2018.
[2] He, Yang, et al. "Soft filter pruning for accelerating deep convolutional neural networks." arXiv preprint arXiv:1808.06866 (2018).
[3] Lin, Mingbao, et al. "Filter Sketch for Network Pruning." arXiv preprint arXiv:2001.08514 (2020).
[4] He, Yang, et al. "Filter pruning via geometric median for deep convolutional neural networks acceleration." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019.
[5] Ye, Jianbo, et al. "Rethinking the smaller-norm-less-informative assumption in channel pruning of convolution layers." arXiv preprint arXiv:1802.00124 (2018).
[6] Lin, Mingbao, et al. "Channel Pruning via Automatic Structure Search." arXiv preprint arXiv:2001.08565 (2020).
[7] Liu, Zechun, et al. "Metapruning: Meta learning for automatic neural network channel pruning." Proceedings of the IEEE International Conference on Computer Vision. 2019.
[8] Lin, Shaohui, et al. "Towards optimal structured cnn pruning via generative adversarial learning." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019.
[9] Singh, Pravendra, et al. "Play and prune: Adaptive filter pruning for deep model compression." arXiv preprint arXiv:1905.04446 (2019).
[11] https://github.com/Eric-mingjie/rethinking-network-pruning
[12] https://github.com/he-y/softfilter-pruning
[13] https://github.com/lmbxmu/FilterSketch
[14] https://github.com/he-y/filter-pruning-geometric-median
[16] https://github.com/lmbxmu/ABCPruner
[17] https://github.com/liuzechun/MetaPruning
