Multi-task Learning Using Uncertainty to Weigh Losses 已经详细描述了贝叶斯模型中几种可建模的不确定性(uncertainty)，并应用了任务依赖/同方差不确定性(Task-dependent or Homoscedastic Aleatoric Uncertainty)来自动学习多任务中的 Loss 权重。本文讨论同为偶然不确定性(Aleatoric Uncertainty)的数据依赖/异方差不确定性(Data-dependent or Heteroscedastic Aleatoric Uncertainty)。需要注意的是，偶然不确定性(Aleatoric Uncertainty)描述的是数据不能解释的信息，只能通过提高数据的精度来消除；而认知不确定性(Epistemic Uncertainty)描述的是模型因为缺少训练数据而存在的未知，可通过增加训练数据解决。
为什么要建模 Heteroscedastic Aleatoric Uncertainty？Learning 算法一个比较致命的问题是，网络能输出预测量，但是网络不知道其预测的不确定性，如目标状态估计中，需要获得观测的协方差矩阵(检测作为观测模块，理论上需要出检测的 Uncertainty，包括 Aleatoric 与 Epistemic Uncertainty，但是 Epistemic Uncertainty 只能通过多次采样近似得到，不能实时应用，所以一般只考虑 Aleatoric Uncertainty 作为观测的不确定性)。尤其在自动驾驶领域，我们不仅关注模型知道什么，更要关注模型不知道什么。
本文通过贝叶斯神经网络来建模 Aleatoric Uncertainty，并分析其应用效果。
1. Aleatoric Uncertainty 建模
针对一批训练数据集\(\{\mathbf{X,Y}\}\)，训练模型 \(\mathbf{y=f^W(x)}\)，在贝叶斯框架下，预测量的后验分布为： \[p\left(\mathbf{y\vert x,X,Y}\right) = \int p\left(\mathbf{y\,|\,f^W(x)}\right) p\left(\mathbf{W\,|\,X,Y}\right)d\mathbf{W} \tag{0}\] 其中 \(p(\mathbf{W\,|\,X,Y})\) 为模型参数的后验分布，描述了模型的不确定性，即 Epistemic Uncertainty；\(p\left(\mathbf{y\,|\,f^W(x)}\right)\) 为观测似然，描述了观测不确定性，即Aleatoric Uncertainty。Epistemic Uncertainty 只能通过近似推断获得，本文不作讨论。
Multi-task Learning Using Uncertainty to Weigh Losses 已经详细推导了 Aleatoric Uncertainty 的建模过程，这里摘抄如下：
\[\mathcal{L}(\mathbf{W}, s_1, s_2) = \frac{1}{2}\mathrm{exp}(-s_1)\mathcal{L}_1(\mathbf{W}) + \mathrm{exp}(-s_2)\mathcal{L}_2(\mathbf{W}) + \mathrm{exp}(\frac{1}{2}s_1) + \mathrm{exp}(\frac{1}{2}s_2) \tag{1}\] 其中 \(\mathcal{L}(\mathbf{W},s_1)\) 为回归项，\(\mathcal{L}(\mathbf{W},s_2)\) 为分类项。
[1][2][3] 中建模的回归项 loss uncertainty 与式(1)有细微出入(可以认为是 Uncertainty 的正则项不同，但是效果类似)，其负log似然为： \[-\mathrm{log}p\left(\mathbf{y}\vert\mathbf{f^W(x)}\right) \propto \frac{1}{2\sigma ^2} \Vert \mathbf{y-f^W(x)} \Vert ^2 + \frac{1}{2}\mathrm{log}\sigma^2 \tag{2}\] 所以其回归项 loss 为： \[\mathcal{L}(\mathbf{W}, s_1) = \frac{1}{2}\mathrm{exp}(-s_1)\mathcal{L}_1(\mathbf{W}) + \frac{1}{2}s_1 \tag{3}\]
1.1. 3D Object Detection by regressing corners[2]
该方案是在俯视图下回归 3D 框的 8 个角点，总共 24 个参数。假设观测为多变量的高斯分布，即： \[\left\{\begin{array}{l} p\left(\mathbf{y}\vert\mathbf{f^W(x)}\right) = \mathcal{N}\left(\mathbf{f^W(x)}, \Sigma(\mathbf{x}) \right) \\ \Sigma(\mathbf{x}) = diag(\sigma _ {\mathbf{x}}^2) \end{array}\tag{4}\right.\] 其中 \(\mathbf{y}\) 是预测的目标框参数，\(\sigma _ {\mathbf{x}}^2\) 是 24 维的向量，表示了观测数据的噪声水平，由式(3)可知，噪声越大，其对 Loss 的作用越小。
如图 1. 所示，同一目标，靠近本车的 corner 点，其 Aleatoric Uncertainty 越小；距离越远，目标被遮挡的越严重，其 Aleatoric Uncertainty 越高。
1.2. 3D Object Detection by regressing location and orientation [3]
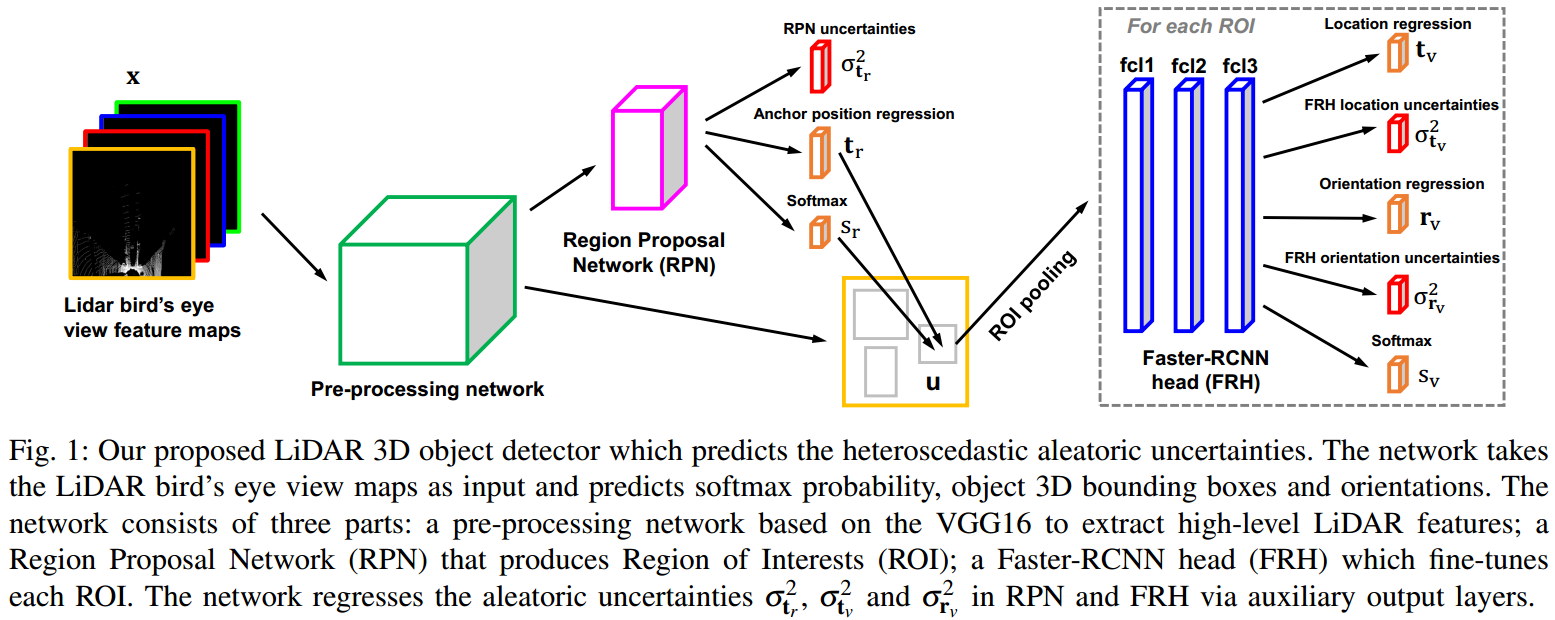如图 2. 所示，网络结构比较简单，这里建模了三种 uncertainty: RPN bbox regression \(\sigma^2_{\mathbf{t_r}}\)；Head 中的 location \(\sigma^2_{\mathbf{t_v}}\)；Head 中的 orientation \(\sigma^2_{\mathbf{r_v}}\)。最终的 Loss 由三项式(3) 以及两项分类 loss 构成。
如图 3. 所示，TV(Total Variance) 与目标状态的关系。对于距离越远，遮挡越严重的目标，其 Aleatoric Uncertainty 会越高，因为其观测到的点云会比较少。
1.3. Semantic Segmentation [1]
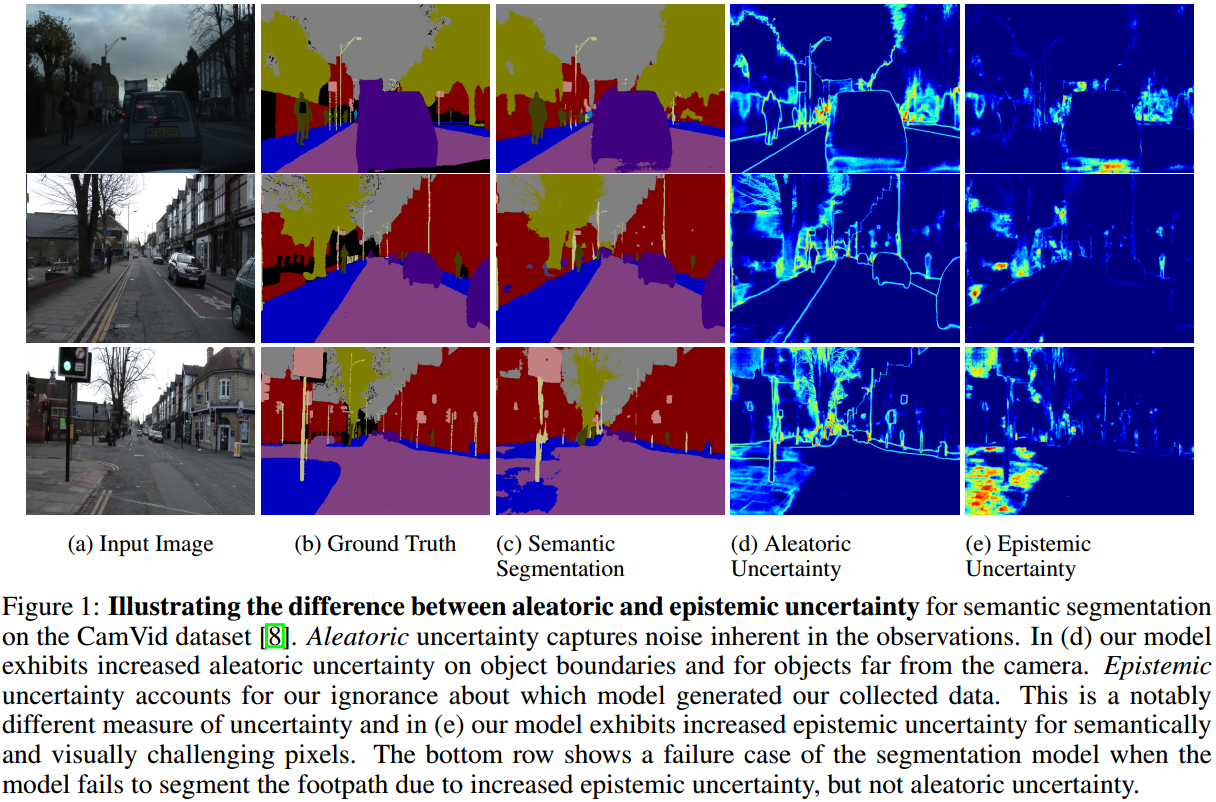如图 4. 所示，Aleatoric Uncertainty 在远处，边缘处较大；而 Epistemic Uncertainty 对没见过的数据/区域较大。
2. Aleatoric Uncertainty 预测
Multi-task Learning Using Uncertainty to Weigh Losses 中 Uncertainty 不需要作为预测输出，可将其设计为网络的 weights，且每个任务都设计为单变量高斯分布的形式。[2][3] 中则将 Uncertainty 设计为网络的输出，且是多变量高斯分布。更一般的，假设模型输出为混合高斯分布： \[\left\{\begin{array}{l} p\left(\mathbf{y}\vert\mathbf{f^W(x)}\right) = \sum_k \alpha_k \mathcal{N}\left(\mathbf{f^W(x)}_{(k)}, \Sigma(\mathbf{x})_{(k)} \right)\\ \sum_k \alpha_k = 1 \end{array}\tag{5}\right.\] 对于 3D Detection 问题，网络输出的 3D 框参数为 \(\mathbf{y}=(x,y,z,l,h,w,\theta)\)，当输出满足 \(K\) 个混合高斯分布时，网络的输出量有：
- \(K\) 组目标框参数预测量 \(\{\mathbf{y}_k\}\)；
- \(K\) 个对数方差 \(\{s_k\}\)；
- \(K\) 个混合高斯模型权重参数 \(\{\alpha_k\}\)；
训练时，找出与真值分布最近的一组预测量，混合高斯模型权重用 softmax 回归并用 cross-entropy loss，找到最相似的分布后，将该分布的方差用式(3)作用于回归的 Loss 项；测试时，找到混合高斯模型最大的权重项，对应的高斯分布，即作为最终的输出分布。这里只考虑了输出 3D 框的一个整体的方差，也可以输出定位方差+尺寸方差+角度方差，只要将该方差作用于对应的 Loss 项即可。当 \(K=1\) 时，就是多变量单高斯模型，一般也够用。
3. Metrics
TODO
4. Reference
[1] Kendall, Alex, and Yarin Gal. "What uncertainties do we need in bayesian deep learning for computer vision?." Advances in neural information processing systems. 2017.
[2] Feng, Di, Lars Rosenbaum, and Klaus Dietmayer. "Towards safe autonomous driving: Capture uncertainty in the deep neural network for lidar 3d vehicle detection." 2018 21st International Conference on Intelligent Transportation Systems (ITSC). IEEE, 2018.
[3] Feng, Di, et al. "Leveraging heteroscedastic aleatoric uncertainties for robust real-time lidar 3d object detection." 2019 IEEE Intelligent Vehicles Symposium (IV). IEEE, 2019.
