检测的发展基本上是从 Anchor-based 这种稀疏的方式到 Anchor-free 这种密集检测方案演进的。相比于 Anchor-free 这种特征层像素级别的回归与分类来检测，更密集的方式，是直接作 Instance Segmentation，然后经过聚类等后处理来得到目标框属性。越密集的检测方案，因为样本较多(一定程度增大了样本空间)，所以学习越困难，但是理论上有极高的召回率。随着一系列技术的发展，如 Focal-loss 等，密集检测性能得以超过二阶段的 Anchor-based 方案，具体描述可参考 Anchor-Free Detection。
本文[1]借鉴 2D Instance Segmentation 思路，提出了一种同时作 3D Instance Segmentation 与 Detection 的方法。百度 Apollo 中的点云分割方法就是俯视图下 Instance Segmentation 然后后处理得到目标 Polygon 与 BBox 的思路，这种方法虽然后处理较为复杂，但是有超参数较少且召回率高的特点。本文算是该方法的 3D 版本(想法很自然，被人捷足先登。。)。
1. Framework
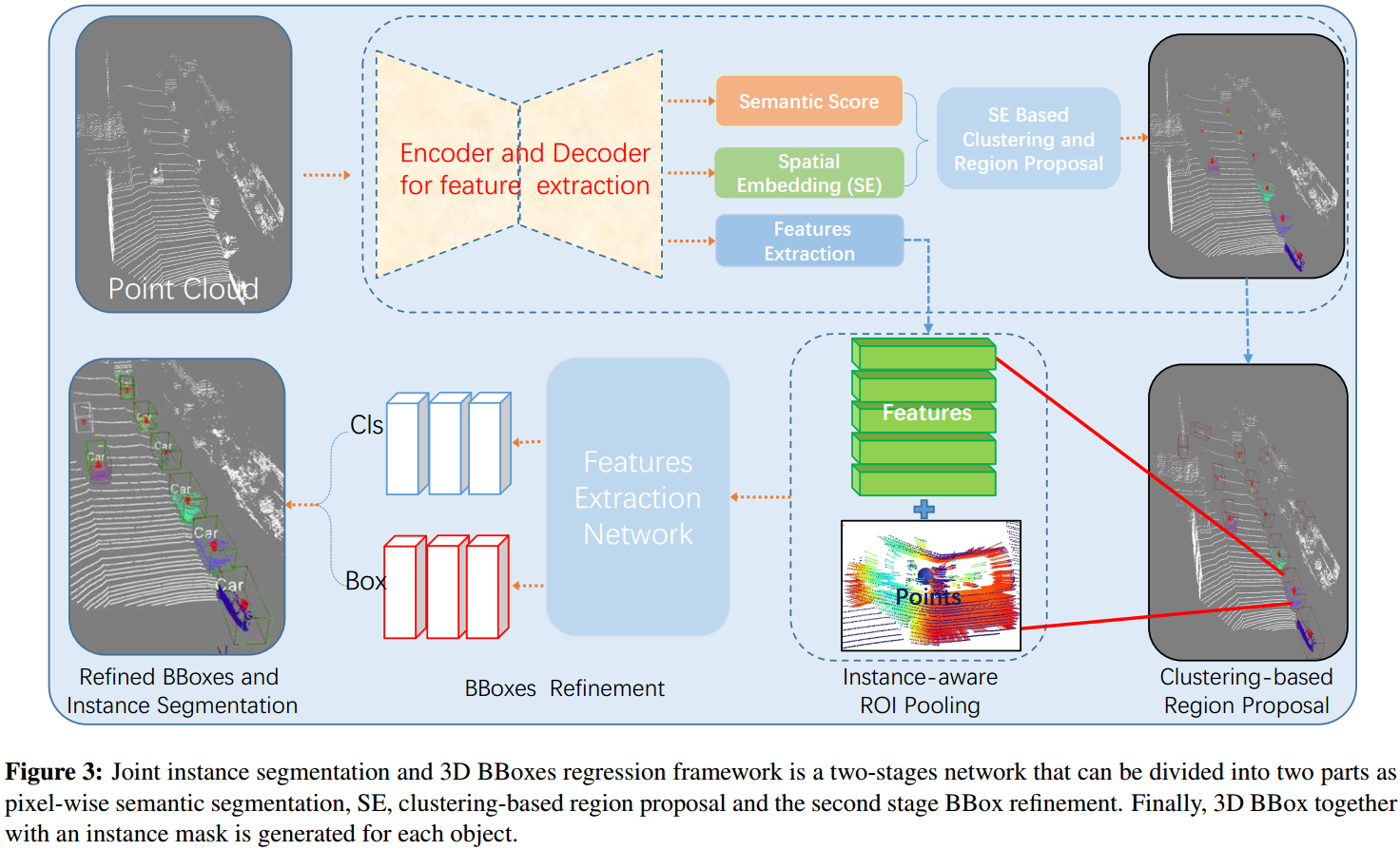如图 1. 所示，本方法由三部分构成：点级别的分类及回归，候选目标聚类，目标框优化。
- 点级别的分类与回归
原始点云经过 Backbone 网络提取局部及全局特征，这里的 Backbone 网络可以是任意能提取点级别特征的网络。基于 Backbone 网络提取的特征，可进行点级别的 Semantic Segmentation 以及 Instance-aware SE(Spatial Embedding)。SE 回归的是每个点距离目标中心点的 offset，该目标的 size，以及该目标的朝向。 - 候选目标聚类
基于预测的 SE，将每个点的位置加上距离目标中心点的 offset，然后可通过简单的聚类算法(如 K-means)即可得到各个目标的点云集合，取 top k 个该点云集合回归的目标框属性，作下一步的目标框进一步优化。 - 目标框优化
基于候选目标聚类得到的目标框，提取目标点集，将其转换到该目标 Local 坐标系下，作进一步的目标框优化。
2. Instance-aware SE
该框架的关键是 Instance-aware SE 的回归，回归量有：距离目标中心点的 offset，目标 size，目标 orientation。传统的 Instance Segmentation 做法是 Feature Embedding，将相同 Instance 的特征拉近，不同的 Instance 的特征推远，这种方法很难构造有效的 Loss 函数，而且同为车的不同 Instance，其特征已经非常接近。而本文 Spatial Embedding 中 offset 的回归量，经过聚类后处理，可以很容易的得到 Instance Segmentation 结果。
Apollo 点云分割的方案中，是在俯视图的 2D 栅格下做的，主要回归量也是这三种，不同的是，2D 栅格是离散的，所以根据 offset 找某一点的中心点时，可以迭代的进行，然后投票出中心点位置，后处理可以做的更细致。这里不做展开，有机会以后写一篇详解。
3. Loss
Loss 项由 Semantic Segmentation，SE，3D BBox regression 组成： \[ L = L _ {seg-cls}+L _ {SE}+L _ {reg} \tag{1}\] Semantic Segmentation Loss 为： \[ L _ {seg-cls}=-\sum _ {i=1}^C (y _ i\mathrm{log}(p _ i)(1-p _ i)^{\gamma}\alpha _ i+(1- y _ i)\mathrm{log}(1-p _ i)(p _ i)^{\gamma}(1-\alpha _ i)) \tag{2}\] 其中 \(C\) 表示类别数；如果某点属于某类，那么 \(y _ i=1\)；\(p _ i\) 表示预测为第 \(i\) 类的概率；\(\gamma,\alpha\) 为超参数。
SE Loss 为： \[ L _ {SE} = \frac{1}{N}\sum _ {i=1}^N\frac{1}{N _ c}\sum _ {i\in ins _ c}^{N _ c}(\mathcal{l} _ {offset}^i+\mathcal{l} _ {size}^i+\mathcal{l} _ {\theta}^i) \tag{3}\] 其中 \(N\) 为 Instance 个数，\(N _ c\) 为内部点数，\(\mathcal{l}\) 为 L1 Smooth Loss。
BBox regression Loss 为 rotated 3D IOU Loss： \[ L _ {reg} = 1-\mathbf{IoU}(B _ g,B _ d)\tag{4}\]
4. Reference
[1] Zhou, Dingfu, et al. "Joint 3D Instance Segmentation and Object Detection for Autonomous Driving." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020.
