PointCloud Feature Extraction

　　机器学习中，特征提取是非常重要的一个环节（认为是最重要的一环也不为过）。对图像数据的特征提取操作已经较为成熟，如卷积；而点云数据由于无序性，所以对其进行高效的特征提取则比较困难。 一个好的点云特征提取操作需要具备以下特征：

• 能提取点云的局部以及全局特征；
• 计算高效；

　　目前已知的点云特征提取方法可分为两大类：Voxel-level，以及 Point-level。Voxel-Level 的特征提取也已经相当成熟，基本思路是将点云空间网格化，每个网格进行手工特征填充或者 Point-level 的特征提取，然后就可以应用标准的 2D/3D 卷积操作进行局部及全局特征提取。这种方法提取的特征细粒度取决于空间栅格化的分辨率，针对点级别的任务（如 semantic segmentation，Scene flow等），其特征的细粒度还是不够的。
　　本文主要介绍 Point-level 的方法，这种方法能提取点级别的局部、全局特征信息，是处理点云的有效手段。这种方法首先要将无序的点云进行一定的结构化组织，由此可分为若干方法，如下阐述。

1. 基于原始三维空间操作

　　在三维空间下进行点的局部特征提取，需要快速找到每个点周围的点，所以需要对点云构建 Kd-tree(或 Ball-tree)，来加速邻近点的快速查询。Kd-tree 的算法复杂度为：

• 构建：\(\mathcal{O}(\mathrm{log}^2n)\)
• 插入：\(\mathcal{O}(\mathrm{log}n)\)
• 删除：\(\mathcal{O}(\mathrm{log}n)\)
• 查询：\(\mathcal{O}(n^{1-\frac{1}{k}}+m)\)，其中 \(m\) 为要查询的最近点个数

1.1. 问题描述

　　设点云集合：\(P=\{p_1,...,p_n\}\in R^{F}\)，每个点有 \(F\) 维的特征，以及每个点的三维坐标为：\(p_i=(x_i,y_i,z_i)\)（注意，坐标也可作为特征包含于 \(F\) 维中）。因为点云的无序性，定义点云集合的最近邻图(k-nearest neighbor graph) \(\mathcal{G=(V,E)}\)，其中 \(\mathcal{V}\) 表示点云中的点，\(\mathcal{E}\) 表示点 \(p_i\) 与最近的 \(k\) 个点 \(P_i^k=\{p_j ^ {i1},...,p_j ^ {ik}\}\) 所构成的有向边集合 \(\{(i,j_{i1}),...,(i,j_{ik})\}\)。由此定义点级别特征提取操作： \[ p_i' = \displaystyle\Box_{j:(i,j)\in\mathcal{E}} h_\Theta(p_i,p_j) \tag{1}\] 其中 \(h _ {\Theta}\) 表示非线性映射函数，将特征空间：\(\mathbb{R} ^ F \times \mathbb{R} ^ F \to \mathbb{R} ^ {F'}\)；\(\Box\) 为用于特征聚合的对称函数。该操作类似图像二维卷积操作，将输入的点云集合：\(P=\{p_1,...,p_n\}\in R^{F}\) 映射到相同点数的：\(P'=\{p_1',...,p_n'\}\in R^{F'}\)。

1.2. \(h,\Box\) 的选择

1.2.1. Euclidean Conv

　　设计 \(h_{\Theta}(p_i,p_j)=\theta_jp_j\)，\(\Box=\sum\)，得到传统的 Euclidean convolution： \[ p_i' = \displaystyle\sum_{j:(i,j)\in\mathcal{E}}(\theta_jp_j) \tag{2}\] 其中 \(\Theta=(\theta_i,...,\theta_k)\) 为滤波器的权重。

1.2.2. PointNet^[1]

　　设计 \(h_{\Theta}(p_i,p_j)=h_{\Theta}(p_i) = \mathrm{MLP}(p_i)\)，\(\Box=\mathrm{MAX} 或 \sum\)，得到 PointNet 中的操作： \[ p_i' = \displaystyle\left\{ \sum|\mathrm{MAX}\right\}(\theta_ip_i) = \displaystyle\left\{\sum|\mathrm{MAX}\right\}\, \mathrm{MLP}(p_i) \tag{3}\] 感知机的权重可以共享。

1.2.3. Deep Parametric Continuous Convoluion^[2]

　　设计 \(h_{\Theta}(p_i,p_j)=\mathrm{MLP}(p_j^{xyz}-p _ i^{xyz})\cdot p _ j^{\mathrm{exclude}\,xyz}\)，\(\Box=\mathrm{\sum}\)，得到 Deep Parametric Continuous Convolution 操作： \[ p_i' = \displaystyle\sum_{j:(i,j)\in\mathcal{E}}\left(\mathrm{MLP}(p_j^{xyz}-p _ i^{xyz})\cdot p _ j^{\mathrm{exclude}\,xyz}\right) \tag{4}\] 根据邻近点的距离，显示的来学习其对中心点的特征贡献。Continuous Fusion Layer 中证明没必要显示的学习，直接将相对距离 Concate 到特征上，隐式的学习同样有效。

1.2.4. PointNet++^[3]/FlowNet3D^[4]/Continuous Fusion Layer^[5]

　　设计 \(h _ {\Theta}(p_i,p_j)=\mathrm{MLP}\,\left(p _ j^{\mathrm{exclude}\,xyz}\oplus (p _ j ^ {xyz}-p _ i^{xyz})\right)\)，\(\Box=\left\{\mathrm{MAX}|\sum\right\}\)，得到 PointNet++/FlowNet3D/Continuous Fusion Layer(前两者是 \(\mathrm{MAX}\)，后者是 \(\sum\) 操作) 中的操作： \[ p_i' = \displaystyle\left\{\mathrm{MAX}|\sum\right\}_{j:(i,j)\in\mathcal{E}}\mathrm{MLP}\,\left(p _ j^{\mathrm{exclude}\,xyz}\oplus (p _ j ^ {xyz}-p _ i^{xyz})\right) \tag{5}\] 将点 \(p_j\) 中的坐标都转换到以中心点 \(p_i\) 为参考的局部坐标。这样能更好的提取局部信息，但是丢失了点的绝对坐标信息。

1.2.5. EdgeConv(DGCNN)^[6]

　　设计 \(h _ {\Theta}(p_i,p_j)=\mathrm{MLP}\,\left(p _ j^{\mathrm{exclude}\,xyz}\oplus (p _ j ^ {xyz}-p _ i^{xyz})\oplus p _ i^{xyz}\right)\)(这里只是猜测是这么做的，EdgeConv paper 中没有具体说怎么做的)，\(\Box=\mathrm{MAX}\)，得到 EdgeConv 中的操作： \[ p_i' = \displaystyle\mathrm{MAX}_{j:(i,j)\in\mathcal{E}}\mathrm{MLP}\,\left(p _ j^{\mathrm{exclude}\,xyz}\oplus( p _ j ^ {xyz}-p _ i^{xyz})\oplus p _ i^{xyz}\right) \tag{6}\] 额外加上点　\(p_i\) 的世界坐标，保留点的全局信息。 　　如图 1. 所示，DGCNN 网络结构与 PointNet 网络差不多，区别就在核心的点特征提取操作。
　　代码实现可参考[14], [15]，其中 [15]是完整的 DGCNN，每次卷积操作都是要在该点的新特征下取寻找 \(k\) 个最近邻，而 [14] 是简化版，最近邻点是固定的，分析代码可知其步骤：

1. 针对每个点 \(p_i\)，首先找到该点最近的 \(k\) 个点及对应的特征，得到 tensor 维度：\(B\times N\times k\times F\);
2. 然后将本点 \(p_i\) 的特征 concate 到对应的 \(k\) 个点特征，得到 tensor 维度： \(B\times N\times k\times 2F\)；
3. 不同层 conv，bn，relu 的作用，得到多个 tensor，其维度：\(B\times N\times k\times \{F'|F'_1,...,F'_s\}\)；
4. 对 \(k\) 个点作最大化聚合，得到各 tensor 维度：\(B\times N\times \{F'|F_1',...,F_s'\}\)
5. 每个点的特征进行 concate，然后作 conv，bn，relu 操作，最终得到点的特征 tensor，维度为 \(B\times N\times F^{final}\)；

该实现与式 (6) 有点出入，该实现没有显示计算本点坐标与对应的 \(k\) 个点坐标的差值。但是总体思想一致。

1.2.6. RandLA-Net^[7]

　　设计 \(h _ {\Theta}(p_i,p_j)=\mathrm{MLP}\,\left(p _ j^{\mathrm{exclude}\,xyz}\oplus\left\Vert p _ j^{xyz}-p _ i^{xyz}\right\Vert\oplus (p _ j ^ {xyz}-p _ i^{xyz})\oplus p _ j^{xyz}\oplus p _ i^{xyz}\right)\)，\(\Box=\sum \mathrm{softmax\,MLP}(h_{\Theta}(p_i,p_j))\)，得到 RandLA-Net 中的操作(详见 RandLA-Net)： \[ p_i' = \displaystyle\sum_{j:(i,j)\in\mathcal{E}}\left(\mathrm{softmax\,MLP'}\,\left(p _ j^{\mathrm{exclude}\,xyz}\oplus\left\Vert p _ j^{xyz}-p _ i^{xyz}\right\Vert\oplus (p _ j ^ {xyz}-p _ i^{xyz})\oplus p _ j^{xyz}\oplus p _ i^{xyz}\right)\right)\cdot \left(\mathrm{MLP}\,\left(p _ j^{\mathrm{exclude}\,xyz}\oplus\left\Vert p _ j^{xyz}-p _ i^{xyz}\right\Vert\oplus (p _ j ^ {xyz}-p _ i^{xyz})\oplus p _ j^{xyz}\oplus p _ i^{xyz}\right)\right) \tag{7}\] 这里的 \(\Box\) 函数称为 Attention Pooling，即将特征维度进行加权求和。

1.2.7. TANet^[12]

　　如图 2. 所示，TANet 中提出了 TA Module，该模块包含三种注意力机制：point-wise，channel-wise，voxel-wise。其中前两种注意力可用于任意点的特征提取。对应的前两种注意力构成了 \(h _ {\Theta}(p_i,p_j)\) 函数： \[h_{\Theta} = \left(\mathrm{MLP_1}(\mathrm{MaxPool_{feats}}\,P_i^k) \times \mathrm{MLP_2}(\mathrm{MaxPool_{points}}\, P_i^k)\right) \cdot P_i^k \tag{8}\] 其中 point-wise attention 为 \(\mathrm{MLP_1}(\mathrm{MaxPool_{feats}}\,P_i^k) = S \in \mathbb{R}^{K\times 1}\)；channel-wise attention 为 \(\mathrm{MLP_2}(\mathrm{MaxPool_{points}}\,P_i^k) = T \in \mathbb{R}^{F\times 1}\)；由此构成 \(M=S\times T\in\mathbb{R}^{K\times F}\)，作为权重作用于 \(P_i^k\)，最后用 \(\sum |\mathrm{MAX}\) 操作对点维度进行特征聚合。注意，这里的 point-wise attention 是与点的顺序有关的，看起来这里经过训练，可以消除点顺序的影响。

1.2.8. PointConv^[13]

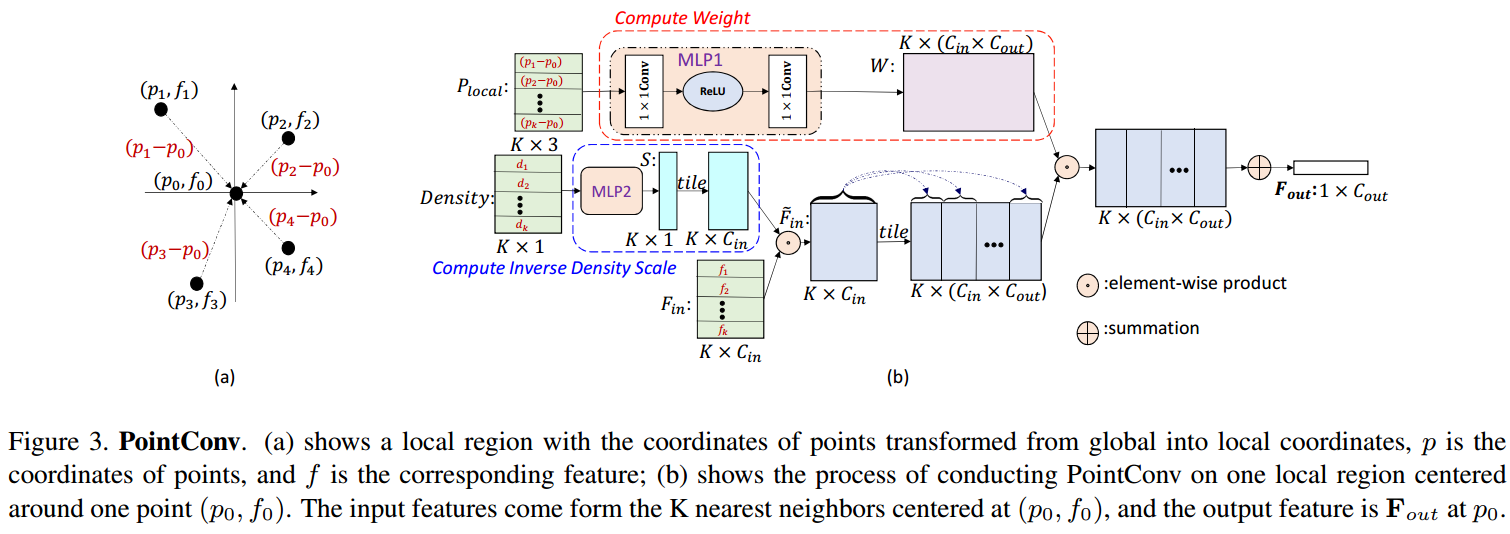
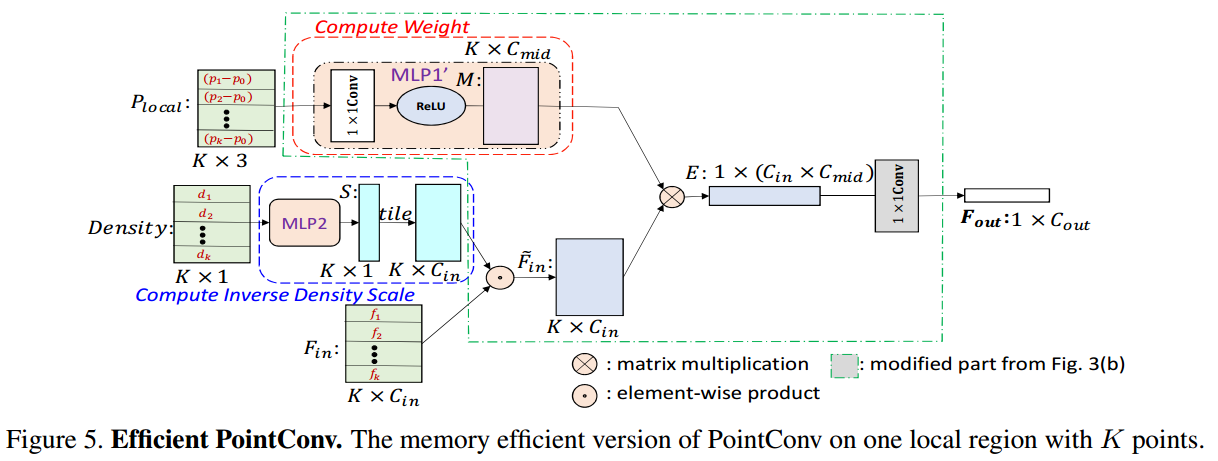　　如图 3. 以及 4. 所示，PointConv 设计的 \(h_{\Theta}\) 有两部分组成。一是根据 \(P_i^k\) 点集计算权重矩阵 \(W\)；二是用核密度函数(Kernel Density Estimation)计算点的密度，然后根据密度计算权重。这里加入基于点密度的权重，是因为，点密度高的区域，需要显式地降低其特征权重，避免最终特征学不到稀疏点的特征。图 4. 是高效版本。

2. 基于映射空间操作

　　基于原始三维空间的点特征提取操作，其算法复杂度直接依赖点数；而如果将其映射到高维空间，则点数只会影响映射与反映射的过程，核心特征提取操作将不受点的个数影响。
　　三维空间下点云无法有序组织，将点云映射到更高维空间，在高维空间下进行结构化组织后，即可应用传统的卷积操作进行特征提取。

2.1. Bilateral Convolutional Layer(BCL^[8])(SPLATNet^[9]/HPLFlowNet^[10])

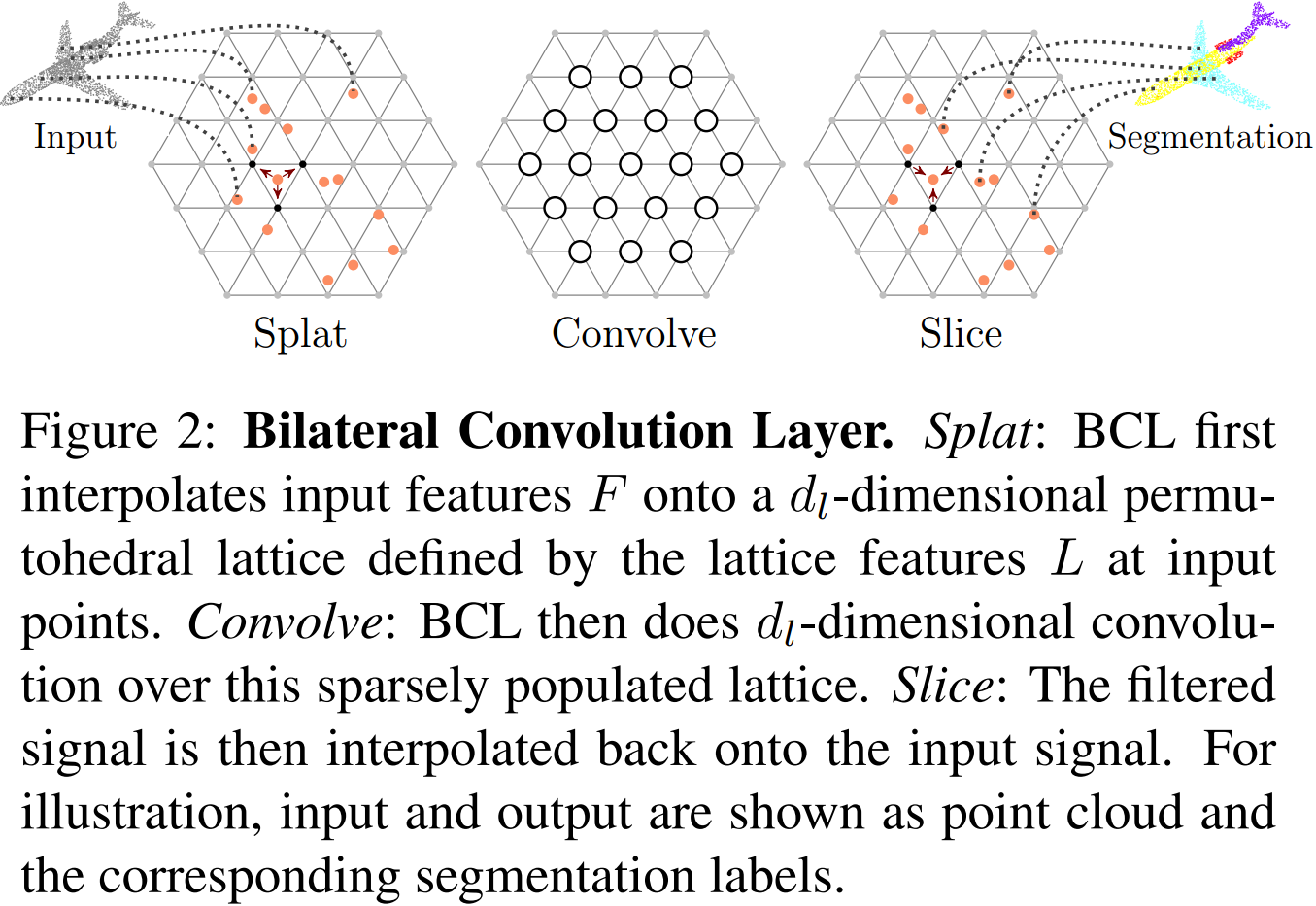　　如图 3. 所示，BCL 操作有三部分组成：

• Splat
  将三维空间的点 \(p_i^{xyz}\) 投影到高维空间，实际操作中直接乘以一个预定义的 \(4\times 3\) 矩阵。4 维空间的晶格顶点聚合晶格内映射点的信息，聚合过程中以映射点与格点的距离作为权重；
• Convolve
  因为晶格空间内空间是栅格化的，所以直接进行传统的 2D 卷积操作；
• Slice
  卷积得到的是晶格空间的特征图，反映射到三维空间，即得到点级别的包含周围信息的特征向量；

　　映射与反映射的操作实现上需要建立哈希表作点的快速查询，需要记录的辅助信息也比较多。后期有时间再对着代码分析。

3. 参考文献

[1] Qi, Charles R., et al. "Pointnet: Deep learning on point sets for 3d classification and segmentation." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017.
[2] Wang, S., Suo, S., Ma, W.C., Urtasun, R.: Deep parameteric convolutional neural networks. In: CVPR (2018)
[3] Qi, Charles Ruizhongtai, et al. "Pointnet++: Deep hierarchical feature learning on point sets in a metric space." Advances in neural information processing systems. 2017.
[4] Liu, Xingyu, Charles R. Qi, and Leonidas J. Guibas. "Flownet3d: Learning scene flow in 3d point clouds." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019.
[5] Liang, Ming, et al. "Deep continuous fusion for multi-sensor 3d object detection." Proceedings of the European Conference on Computer Vision (ECCV). 2018.
[6] Wang, Yue, et al. "Dynamic graph cnn for learning on point clouds." ACM Transactions on Graphics (TOG) 38.5 (2019): 146.
[7] Hu, Qingyong, et al. "RandLA-Net: Efficient Semantic Segmentation of Large-Scale Point Clouds." arXiv preprint arXiv:1911.11236 (2019).
[8] Kiefel, Martin, Varun Jampani, and Peter V. Gehler. "Permutohedral lattice cnns." arXiv preprint arXiv:1412.6618 (2014).
[9] Su, Hang, et al. "Splatnet: Sparse lattice networks for point cloud processing." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018.
[10] Gu, Xiuye, et al. "Hplflownet: Hierarchical permutohedral lattice flownet for scene flow estimation on large-scale point clouds." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019.
[11] Xie, Liang, et al. "PI-RCNN: An Efficient Multi-sensor 3D Object Detector with Point-based Attentive Cont-conv Fusion Module." arXiv preprint arXiv:1911.06084 (2019).
[12] Liu, Zhe, et al. "TANet: Robust 3D Object Detection from Point Clouds with Triple Attention." arXiv preprint arXiv:1912.05163 (2019).
[13] Wu, Wenxuan, Zhongang Qi, and Li Fuxin. "Pointconv: Deep convolutional networks on 3d point clouds." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019.
[14] https://github.com/WangYueFt/dcp/blob/master/model.py
[15] https://github.com/WangYueFt/dgcnn/blob/master/pytorch/model.py