点云的 Scene Flow 与 Semantic 一样是一个较低层的信息，通过 Point-Wise Semantic 信息可以作物体级别的检测，这种方式有很高的召回率，且超参数较少。同样，通过 Point-Wise Scene Flow 作目标级别的运动估计(当然也可作物体点级别聚类检测的线索)，也会非常鲁棒。本文[1] 将点级别/Voxel 级别的 Scene Flow 与 3D 目标检测融合在一起，作物体级别的运动估计，工作系统性较强。
1. 问题描述
设 \(t\) 时刻点云 \(\mathbf{P} _ t\in\mathbb{R}^{M\times 3}\)，那么需要求解的未知量有：
- 每个点的 Scene Flow: \(\mathbf{v} _ i\in\mathbb{R} ^3\);
- 每个点集的 Rigid Motion: \(\mathbf{R} _ i\in\mathbb{R}^{3\times 3}\)，\(\mathbf{t} _ i\in\mathbb{R}^{3}\);
- 每个物体的 3D 属性：Location，Orientation，Size，Rigid Motion;
2. 算法框架
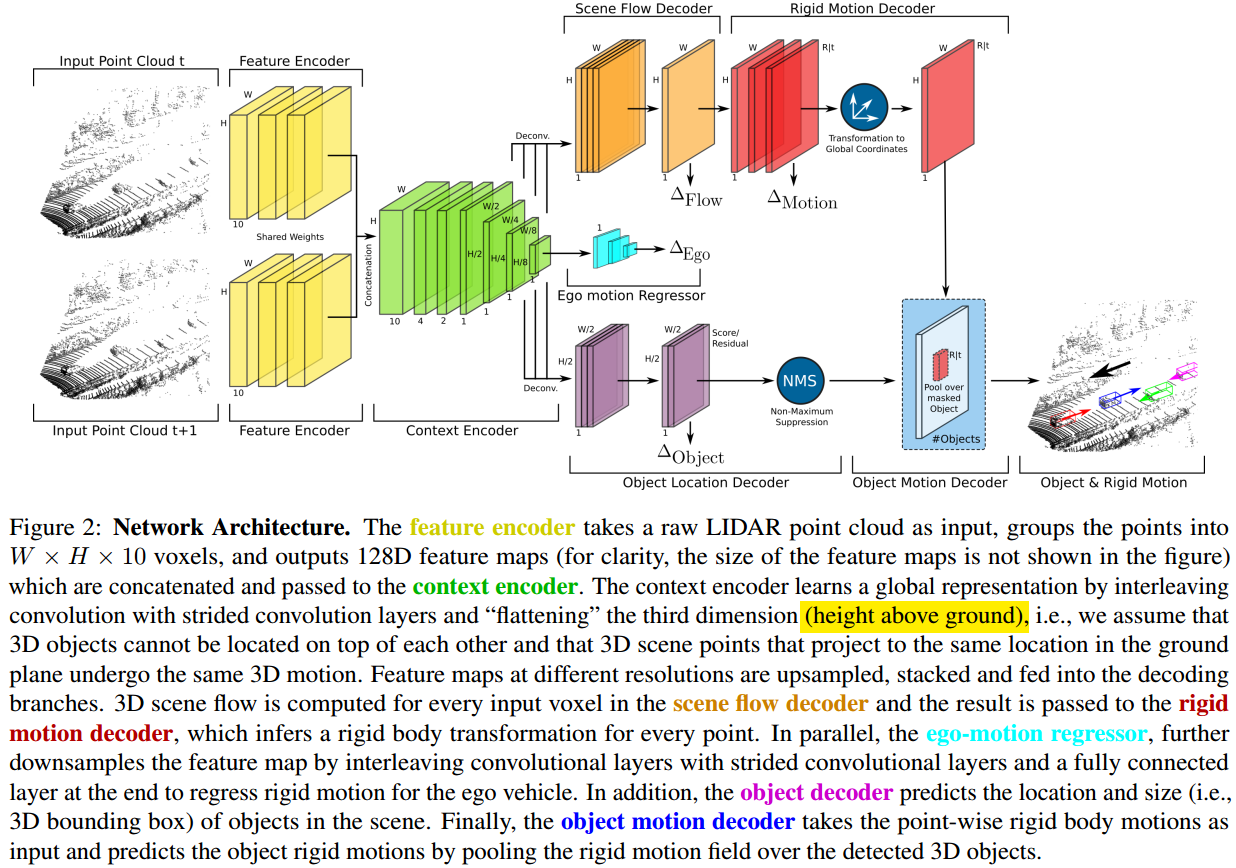如图 1. 所示，PointFlowNet 由四部分组成，分别为：Feature Encoder，Scene Flow/Ego-motion Estimation and 3D Object Detection，Rigid Motion Estimation，Object Motion Decoder。Feature Encoder 将前后帧点云栅格化后作特征提取，然后 Context Encoder 作进一步的特征融合去提取；输出的特征第一个分支作 Voxel 级别的 Scene Flow 预测，进一步作每个点的 Rigid Motion 预测(每个点属于对应物体的 Motion 在该 Voxel 坐标系下的表示)；第二个分支作 Ego-Motion 的预测；第三个分支作 3D 目标检测，进一步作目标的 Motion Decoder。
2.1. Feature Encoder
不同的点云特征提取方式都可采用，本文采用传统的 Bird-View Voxel 表示方式，然后作 2D/3D 卷积。同时还需要将前后帧的点云作特征融合，这里也完全可以采用 FlowNet3D 的特征提取形式。
2.2. Scene Flow/Rigid Motion Decoder
Scene Flow 是作 Bird-View 下 Voxel 级别的场景流预测，然后再预测 Rigid Motion。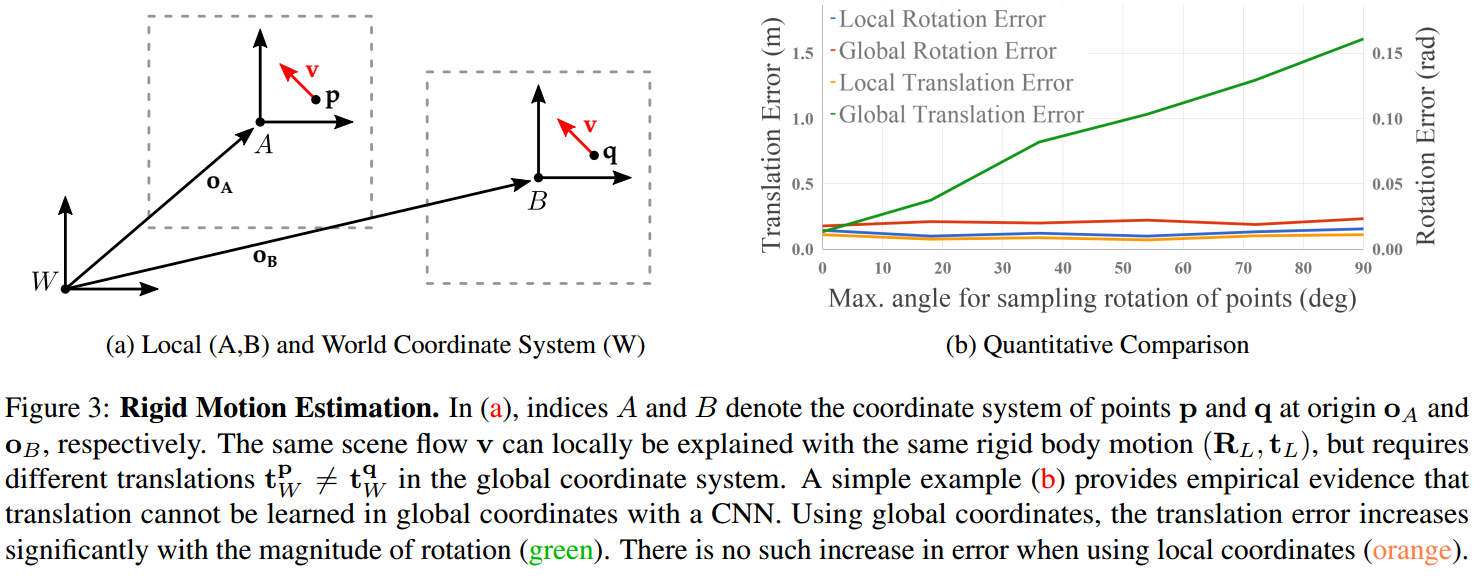 
如图 2. 所示，世界坐标系 \(\mathbf{W}\) 下点 \(\mathbf{p}\) 的 scene flow 表示为 \(\mathbf{v}\)，刚体物体的局部坐标系从 \(\mathbf{A}\) 经过 \((\mathbf{R _ A, t _ A})\) 运动到 \(\mathbf{B}\) ，那么其 scene flow 可表示为： \[\mathbf{v=[R _ A(p-o _ A)+t _ A]-(p-o _ A)} \tag{1}\] 本文论证了两个定理：
- scene flow 只能通过刚体局部坐标系的运动导出，不能直接通过世界坐标系下的刚体运动导出(除非运动无旋转量)。所以如图 1. 所示，通过 scene flow 预测出的 voxel motion 是局部坐标系下的，还需通过坐标变换到世界坐标系下。这里每个 Voxel 预测量的局部坐标系采用 Voxel 中心点。作目标运动估计时，"世界坐标系"其实可以定义为物体坐标系(Voxel 为局部坐标系)，最后再通过 Ego-motion 变换到世界坐标系。
- 不管是局部坐标系 \(\mathbf{A}\) 还是 \(\mathbf{B}\)，都能导出 scene flow。
如图 2. 所示，实验也验证了 scene flow 不能直接学习到世界坐标系下的 translation 运动。
2.3. Ego-motion Regressor
根据前后帧的点云回归本车的运动(ego-motion)，ego-motion 建立局部坐标系与世界坐标系的联系。如果有更精准的外部模块估计的 ego-motion，则可以直接替换采用。
2.4. 3D Object Detection and Object Motion Decoder
Bird-view 下 Voxel 后的 3D 检测方法很多，可以是 Anchor-based，Anchor-free，Semantic Segmentation 等方法，其中如果采用 Semantic Segmentation + cluster 方法，那么 scene flow 的结果也可作为 cluster 的线索。
有了 3D 目标以及目标内 Voxel 的 Rigid Motion 后，取平均或中值即可得到目标的 Motion。
Voxel Rigid Motion 可以有两种回归方法：
- translation 真值为实际该 Voxel 的位移，rotation 为对应刚体的旋转量；
- translation 与 rotation 均为对应刚体的位移与旋转量；
我理解的本文是采用方法 1. 这种形式，这种形式的好处是回归的就是真实 Voxel 的位移，与输入的特征是 Voxel 级别对应的，但是简单的对目标内的 Voxel 取平均或中值只是目标位移的近似，实际目标的真实位移应该为旋转中心 Voxel 的位移。而方法 2. 是物体级别的回归量，均值即可反应物体的运动，只要构建物体级别的 Loss，用 Voxel 去学习物体级别的运动应该问题不大，所以可能方法 2. 更合理。
3. Loss Functions
采用 Voxel 级别的 Loss，总的 Loss 为： \[\mathcal{L}=\alpha\mathcal{L} _ {flow}+\beta\mathcal{L} _ {rigmo} + \gamma\mathcal{L} _ {ego}+\mathcal{L} _ {det}\tag{2}\] 这四部分具体的形式为：
- Scene Flow Loss
对于有效的 Voxel，作预测值与真值的 \(\mathcal{l} _ 1\) 误差： \[\mathcal{L} _ {flow}=\frac{1}{K}\sum _ j\Vert \mathbf{v} _ j-\mathbf{v} _ j ^ * \Vert \tag{3}\] - Rigid Motion Loss
对于有效的 Voxel，作预测值与真值(真值有两种形式，详见 2.4 讨论)的 \(\mathcal{l} _ 1\) 误差： \[\mathcal{L} _ {rigmo} = \frac{1}{K}\sum _ j\Vert\mathbf{t} _ j-\mathbf{t} _ j^ * \Vert+\lambda\Vert\theta _ j-\theta _ j^ * \Vert\tag{4}\] - Ego-motion Loss
同样的对预测值与真值作 \(\mathcal{l} _ 1\) Loss: \[\mathcal{L} _ {ego}=\Vert\mathbf{t} _ {BG}-\mathbf{t} _ {BG}^ * \Vert+\lambda\Vert\theta _ {BG}-\theta _ {BG}^ * \Vert \tag{5}\] - Detection Loss
不作赘述。
4. Reference
[1] Behl, Aseem, et al. "Pointflownet: Learning representations for rigid motion estimation from point clouds." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019.
