基于点云的神经网络学习方法在 Deep Learning for 3D Point Clouds 中已经有较为详细的描述，从网络结构上看，可分为 Multi-view-based(Projection-based)，Volumetric-based，Point-based 等三种方法。其中 Point-based 方法对点云的信息提取分辨率最高，但是前两种将点云空间离散化的方法更容易学到特征信息。所以如何结合这两种网络结构来更有效得学习点云特征就显得非常重要。
此外，Rethinking of Sparse 3D Convolution 中阐述了 Sparse Convolution 相比传统卷积在点云特征学习中的优势，其能更有效学习点云特征信息。
本文[1] 提出了一种 Sparse Point-Voxel 的基本网络结构，并采用 NAS 网络搜索方法来搜索最优的卷积通道数量及深度。
1. Sparse Point-Voxel Convolution(SPVConv)
Voxel-based 特征提取会损失信息源，但是提取效率较高；Point-based 能保留信息分辨率，但是提取效率较低。本文设计的 SPVConv 则融合了二者的优势。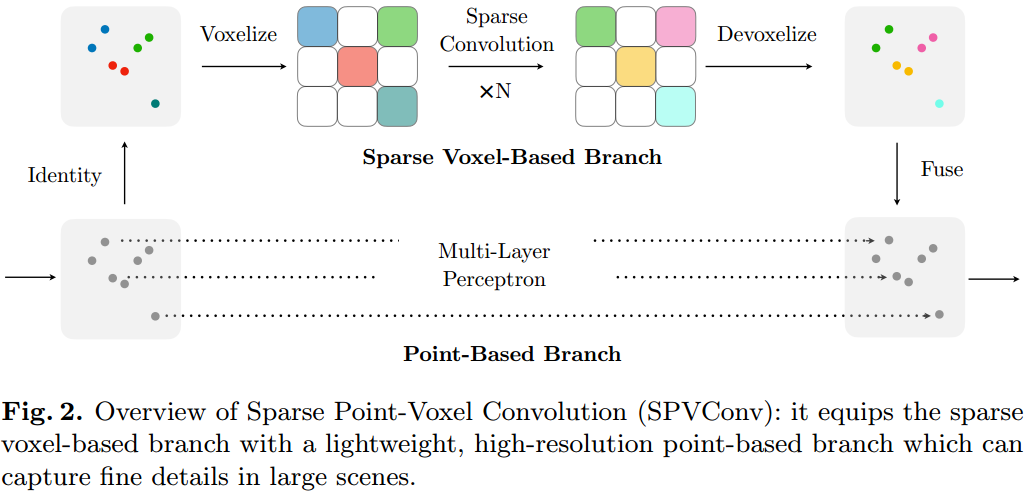 
如图 1. 所示，网络模块由两个分支组成，Point-Based 分支对点云进行点级别的 MLP 运算；Sparse Voxel-Based 分支将点云进行体素化，然后用稀疏卷积进行特征提取，然后反体素化得到点级别的特征。最后将二者提取的特征融合到一起。
数学描述上，首先是数据表示：
- 稀疏体素化张量(Sparse Voxelized Tensor)表示为 \(\mathbf{S}=\{(\mathbf{p} _ m ^ s,\mathbf{f} _ m ^ s),v\}\)，其中 \(\mathbf{p} _ m ^ s=(\mathbf{x} _ m ^ s,\mathbf{y} _ m ^ s, \mathbf{z} _ m ^ s)\) 表示第 \(m\) 个体素的 3D 坐标，\(\mathbf{f} _ m ^ s\) 表示其特征向量；\(v\) 是该层级下的体素尺寸；
- 点云张量(Point Cloud Tensor)表示为 \(\mathbf{T} = \{(\mathbf{p} _ k ^ t,\mathbf{f} _ k ^ t)\}\)，其中 \(\mathbf{p} _ k=(\mathbf{x} _ k, \mathbf{y} _ k,\mathbf{z} _ k)\) 表示第 \(k\) 个点的 3D 坐标，\(\mathbf{f} _ k\) 为其特征向量。
然后将点云进行稀疏体素化映射，计算每个体素的特征向量：
\[\hat{\mathbf{p}} _ k ^ t=(\hat{\mathbf{x}} _ k ^ t,\hat{\mathbf{y}} _ k ^ t,\hat{\mathbf{z}} _ k ^ t) = \left(\mathrm{floor}(\mathbf{x} _ k ^ t/v),\mathrm{floor}(\mathbf{y} _ k ^ t/v),\mathrm{floor}(\mathbf{z} _ k ^ t/v)\right) \tag{1}\] \[\mathbf{f} _ m ^ s=\frac{1}{N _ m}\sum _ {k=1} ^ n\mathbb{1}[\hat{\mathbf{x}} _ k ^ t=\mathbf{x} _ m ^ s,\hat{\mathbf{y}} _ k ^ t=\mathbf{y} _ m ^ s,\hat{\mathbf{z}} _ k ^ t=\mathbf{z} _ m ^ s]\cdot\mathbf{f} _ k ^ t\tag{2}\] 直接计算的复杂度为 \(\mathcal{O}(mn)\)，为了实时计算，需要对体素化和反体素化进行哈希索引。哈希表的 key 为 3D 坐标，value 为稀疏张量的 index，所以最终的建立哈希表和查询复杂度为 \(\mathcal{O}(m+n)\)。
对于反体素化，采用 trilinear interpolation，在稀疏体素中采样得到点级别的特征。该特征与点级别 MLP 得到的特征作特征维度的串联操作，即得到提取的点特征向量。
2. 3D-NAS
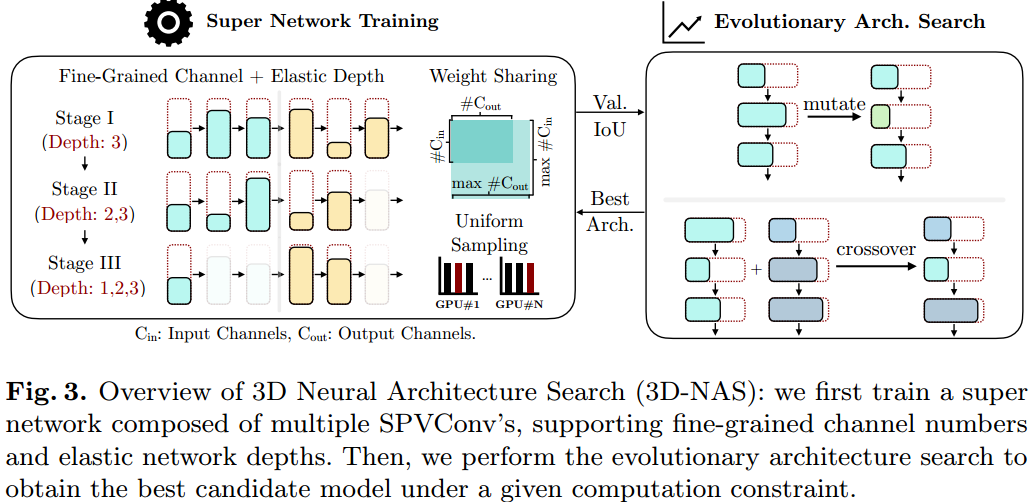
以 SPVConv 模块为基础结构，搜索最优的网络 channel 数，以及网络深度。卷积核固定为 3x3。
搜索策略为：首先训练一个最大的网络，那么搜索的子网络权重可以从大网络中继承，具体搜索策略可参考代码。
3. Reference
[1] Tang, Haotian, et al. "Searching efficient 3d architectures with sparse point-voxel convolution." European Conference on Computer Vision. Springer, Cham, 2020.
