目前业界比较流行的基于激光雷达的 SLAM 是 LOAM，其中 Mapping 又是非常重要的一环，LOAM 提取 Edge 点与 Surf 点然后建立以 Voxel 约束点个数的点云地图，该地图用于 Lidar Odometry 时的匹配定位。实际应用于工业界时，Mapping 的数据结构设计及存取管理对整体系统的效率至关重要，具体可优化的细节以后再写文阐述。
本系列文章[1][2] 提出了一种基于 Surfel 和语义信息的建图及定位方法。整体框架与 LOAM 类似，只是这里只用了面区域的特征点，其它模块，如优化方式，也有很大的差异。
1. SuMa
设 \(A\) 坐标系下的点 \(p _ A\)，\(B\) 坐标系下的点 \(p _ B\)，其变换矩阵 \(T _ {BA}\in\mathbb{R}^{4\times 4}\)，使得 \(p _ B = T _ {BA} p _ A\)。变换矩阵 \(T _ {BA}\) 又由 \(R _ {BA}\in\mathbf{SO}(3)\) 和 \(t _ {BA}\in\mathbb{R}^3\) 构成。设每帧点云的雷达坐标系为 \(C _ k,k\in\{0,...,t\}\)，那么 Lidar Odometry 要求解的问题就是当前雷达坐标系在世界坐标系下的表示： \[T _ {WC _ t} = T _ {WC _ 0}T _ {C _ 0C _ 1}\cdots T _ {C _ {t-1}C _ t} \tag{1}\] 其中 \(T _ {WC _ 0}\) 为已标定的变换矩阵。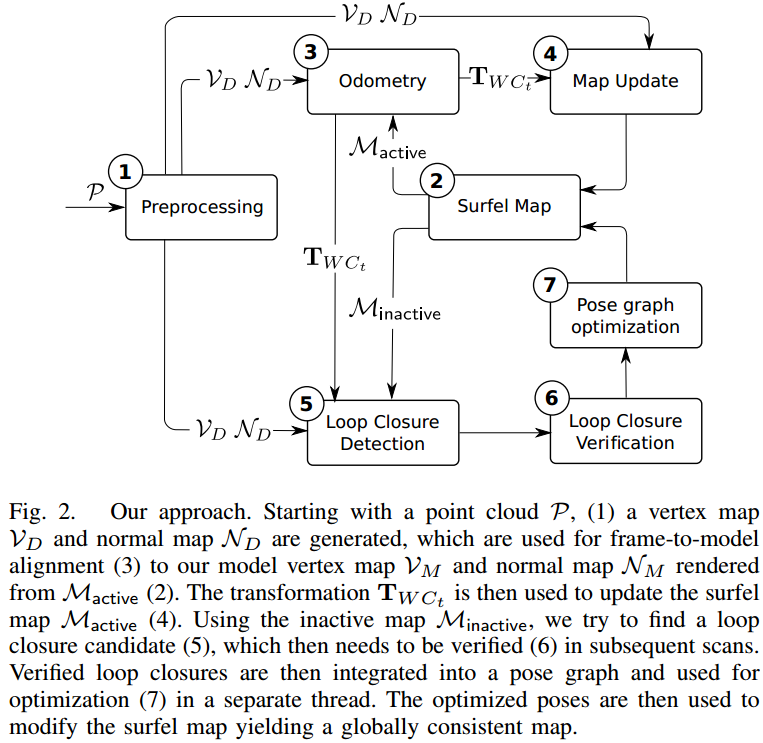 
如图 1. 所示，SuMa 根据点云 \(\mathcal{P} = \{p\in\mathbb{R}^3\}\) 估计 \(T _ {WC _ t}\) 的步骤为：
- 当前帧地图计算。将当前帧的三维点云投影到二维，得到顶点图 \(\mathcal{V} _ D\)，以及计算对应的法向量图 \(\mathcal{N} _ D\)；
- 当前地图计算。对上一帧优化出的 Surfel Map \(\mathcal{M} _ {active}\) 作顶点图和法向量图的渲染 \(\mathcal{V} _ M,\mathcal{N} _ M\)；
- 位姿计算。根据 \(\mathcal{V} _ D, \mathcal{N} _ D\) 以及 \(\mathcal{V} _ M,\mathcal{N} _ M\) 作 frame-to-model 的 ICP 匹配，得到相对位姿 \(T _ {C _ {t-1}C _ t}\)，最后用式(1)计算当前帧在世界坐标系下的位姿态 \(T _ {WC _ t}\)；
- 地图更新。根据 \(T _ {WC _ t}\)，更新 Surfel Map \(\mathcal{M} _ {active}\)：初始化首次观测的区域，优化更新再次观测的区域；
- 闭环检测。在未激活的 Surfel Map \(\mathcal{M} _ {inactive}\) 中搜索当前帧地图的匹配；
- 闭环检测验证。在接下来 \(\Delta _ {verification}\) 时间内，验证闭环检测的有效性，如果有效，那么加入之后的位姿图优化；
- 位姿图优化。另一个线程作位姿图优化，输入信息是前后帧的相对位姿里程计以及闭环检测的相对位姿结果，类似 AVP-SLAM 中的位姿图优化。优化后的位姿用来更新 Surfel Map。
1.1. Preprocessing
与 RangeNet++[3] 中对点云的表示一样，顶点图 \(\mathcal{V} _ D\) 的计算方法为： \[\left(\begin{matrix}
u\\
v\\
\end{matrix}\right)=
\left(\begin{matrix}
\frac{1}{2}[1-\mathrm{arctan}(y,x)\cdot \pi ^ {-1}]\cdot w\\
[1-(\mathrm{arcsin}(z\cdot r ^ {-1})+f _ {up})f ^ {-1}]\cdot h
\end{matrix}\right)
\tag{2}\] 其中 \(r = \Vert p\Vert _ 2\) 为点的距离，\(f = f _ {up} + f _ {down}\) 是雷达的上下视野角，\(w,h\) 为顶点图的宽和高。然后基于 \(\mathcal{V} _ D\) 计算每个顶点的法向量，得到法向量图 \(\mathcal{N} _ D\): \[\mathcal{N} _ D((u,v)) = \left(\mathcal{V} _ D((u+1,v))-\mathcal{V} _ D((u,v))\right)\times \left(\mathcal{V} _ D((u,v+1))-\mathcal{V} _ D((u,v))\right) \tag{3}\] 其中只计算坐标点 \((u,v)\) 有顶点的法向量。因为 \(u\) 方向物理世界是环状的，所以对边界作环向处理。这种法向量计算的 \(\mathcal{N} _ D\) 由较大噪声，但是实验发现对 Frame-to-Model 的 ICP 匹配不会产生精度影响。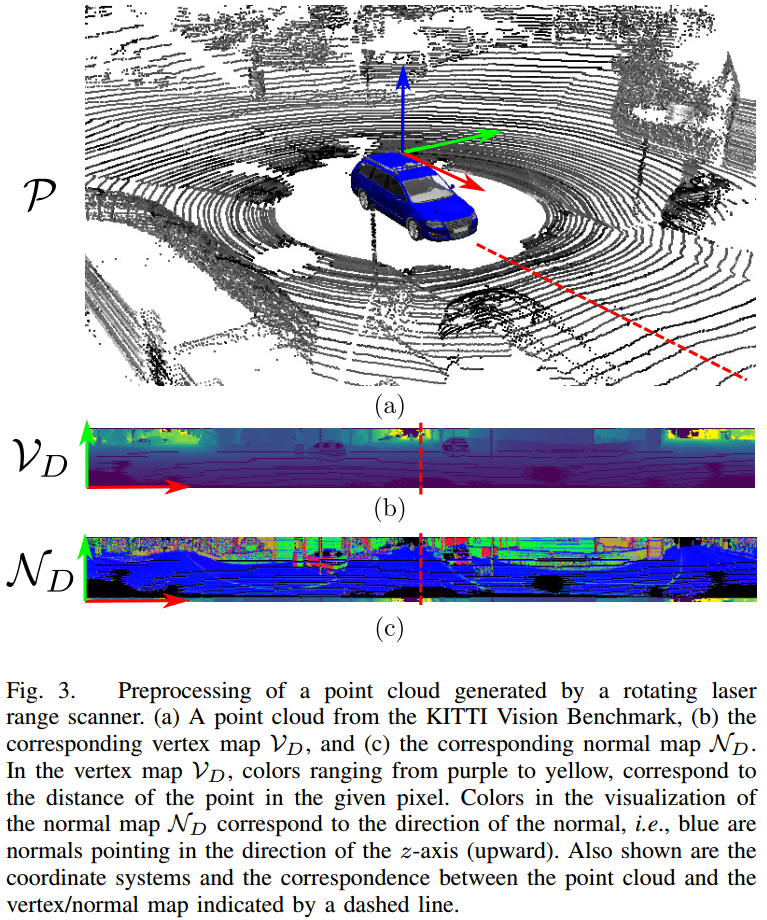 
顶点图 \(\mathcal{V} _ D\) 与法向量图 \(\mathcal{V} _ N\) 的可视化结果如图 2. 所示。
1.2. Map Representation
不同于 LOAM 中采用了 Edge 和 Surf 两种特征来表示地图，本文只用 Surfel 来表示地图 \(\mathcal{M}\)。LOAM 中计算了每个点的曲率，然后将其归为 Edge 或是 Surf，实际工程应用中，为了存储的高效性，首先将点云地图体素化，然后将体素内的特征点用 Mean，Normal，协方差矩阵的 EigenVector 等信息来存储，Normal 可用来表征 Surf 特征点，EigenVector 则可用来表征 Edge 特征点，这块具体的细节以后开文再详细阐述。
本文的 Surfel Map 自然就提取了点云的 Surf 特征，每个Surfel 可以用位置 \(v _ s\in\mathbb{R} ^ 3\)，法向量 \(n _ s\in\mathbb{R} ^ 3\)，半径 \(r _ s\in\mathbb{R}\) 来表示。此外每个 Surf 包含两个时间戳：首次建立的时间 \(t _ c\)，以及最新更新的时间 \(t _ u\)。然后采用贝叶斯滤波方法(详见 Grid-Mapping)，定义及计算 Surfel 特征的稳定概率： \[\begin{align}
l _ s ^ {(t)} &= l _ s ^ {t-1} + \mathrm{log}(p\cdot (1-p) ^ {-1}) - \mathrm{log}(p _ {prior}\cdot (1-p _ {prior}) ^ {-1})\\
&= l _ s ^ {t-1} + \mathrm{odds}(p) - \mathrm{odds}(p _ {prior})\\
&= l _ s ^ {t-1} + \mathrm{odds}\left(p _ {stable}\cdot \mathrm{exp}\left(-\frac{\alpha ^ 2}{\sigma _ {\alpha} ^ 2}\right)\mathrm{exp}\left(-\frac{d ^ 2}{\sigma _ d ^ 2}\right)\right) - \mathrm{odds}(p _ {prior})
\end{align} \tag{4}\] 其中 \(p _ {stable}, p _ {prior}\) 分别为测量为 surfel 是 stable 的概率，以及先验概率。\(\sigma ^ 2\) 为测量噪声方差。\(\alpha\) 为测量的 Surfel 法向量与对应的地图中 Surfel 法向量的夹角，\(d\) 则为测量的 Surfel 与对应的地图中 Surfel 的距离。
每个 Surfel 的位置及法向量都是以建立时的位置作为参考系，即 \(C _ {t _ c}\)。这样经过全局位姿优化后，就不需要重新建图，只需要通过 \(T _ {WC _ {t _ c}}\) 将 Surfel 地图更新到世界坐标系即可。
\(\mathcal{M} _ {active}\) 与 \(\mathcal{M} _ {inactive}\) 的区分也比较简单：\(\mathcal{M} _ {active}\) 定义为最近更新的 Surfels，即 \(t _ u\geq t - \Delta _ {active}\)；\(\mathcal{M} _ {inactive}\) 则定义为不是最近建立的 Surfels，即 \(t _ c< t - \Delta _ {active}\)。Odometry 只在 \(\mathcal{M} _ {active}\) 中作匹配计算，Loop Closure 则只在 \(\mathcal{M} _ {inactive}\) 中搜索。
1.3. Odometry Estimation
里程计是将当前帧点云与地图点云匹配的过程。将上一时刻的地图 \(\mathcal{M} _ {active}\) 渲染成上一时刻局部坐标系下的顶点图 \(\mathcal{V} _ M\) 与法向量图 \(\mathcal{N} _ M\) 形式。然后采用 point-to-plane 的 ICP 匹配方法，其最小化误差为： \[ E(\mathcal{V} _ D,\mathcal{V} _ M, \mathcal{N} _ M) = \sum _ {u\in\mathcal{V} _ D}n _ u ^ T\cdot\left(T _ {C _ {t-1}\;C _ t}^{(k)}\;u-v _ u\right) ^ 2 \tag{5}\] 其中 \(u\in\mathcal{V} _ D\)，\(v _ u\in\mathcal{V} _ M,n _ u\in\mathcal{N} _ M\) 是地图上对应关联上的点，关联过程为： \[\begin{align}
v _ u &= \mathcal{V} _ M\left(\Pi\left(T _ {C _ {t-1}\;C _ t}^{(k)}\;u\right)\right)\\
n _ u &= \mathcal{N} _ M\left(\Pi\left(T _ {C _ {t-1}\;C _ t}^{(k)}\;u\right)\right)
\end{align} \tag{6}\] 其中 \(T _ {C _ {t-1}\;C _ t} ^ {(t)}\) 为 frame-to-model ICP 得到的里程计估计的相对位姿。\(\Pi(u)\) 是特征点的关联方式，LOAM 中根据前后线束的关系来寻找关联方式，本方案则采用直接坐标映射的方式。因为点云均投影到了前视图，所以可根据坐标直接搜索关联，这也是本方案最重要的优势之一。具体的，如图对应的地图顶点图中没有顶点，或者地图法向量点没有定义，那么忽略该待关联的特征点；对于关联的特征点对距离大于 \(\sigma _ {ICP}\) 或是法向量夹角大于 \(\theta _ {ICP}\) 的情况，则认为是离群点，不计入误差项。ICP 初始化为上一帧的相对位姿结果。
该问题是典型的非线性最小二乘问题，可在李空间下对位姿进行线性化并用 Gaussian-Newton 求解，这里不做展开。
1.4. Map Update
得到里程计估计的相对位姿后，要将当前帧的特征点更新到地图中，即要确定哪些 Surfel 要更新，哪些要重新构建新的 Surfel。对于 \(v _ s\in\mathcal{V} _ D\)，首先计算其面元的半径： \[ r _ s = \frac{\sqrt{2}\Vert v _ s\Vert _ 2\cdot p}{\mathrm{clam}(-v _ s ^ T n _ s\cdot\Vert v _ s\Vert _ 2 ^ {-1}, 0.5, 1.0)} \tag{7}\] 其中 \(p=\mathrm{max}(w\cdot f _ {horiz} ^ {-1}, h\cdot f _ {vert} ^ {-1})\)。根据式(2)，每个 \(v _ s\) 均能找到地图中对应的 Surfel \(s '\)。然后通过 \(\vert n _ {s'} ^ T(v _ s-v _ {s'})\vert < \sigma _ M \;\mathrm{and}\; \Vert n _ s\times n _ {s'}\Vert < \mathrm{sin}(\theta _ M)\) 判定当前帧的 Surfel 与地图中的 \(s'\) 是否一致：
- 如果一致。那么更新地图中的 Surfel，如果估计的半径更准，那么也更新： \[\begin{align} v _ {s'} ^ {(t)} &= (1-\gamma)\cdot v _ s + \gamma\cdot v _ {s'} ^ {(t-1)}\\ n _ {s'} ^ {(t)} &= (1-\gamma)\cdot n _ s + \gamma\cdot n _ {s'} ^ {(t-1)}\\ r _ {s'} ^ {(t)} &= r _ s, \; \mathrm{if} \; r _ s < r _ {s'} \end{align} \tag{8}\]
- 如果不一致。那么将地图中匹配上的 Surfel 作 Stable 概率衰减，然后创建新的 Surfel。如果地图中没有匹配的 Surfel，那么也创建新的 Surfel。
最后将 Stable 概率较小的 Surfel 以及时间较早的 Surfel 删除，以此删除动态障碍物特征点以及较老的无关的特征点。
1.5. Loop Closures
检测到闭环后就可以作 Pose Graph 优化。闭环检测由检测与验证两部分组成，检测的过程为在未激活的地图 \(\mathcal{M} _ {inactive}\) 中找到一个最相近的位姿： \[ j ^ * = \mathop{\arg\min}\limits _ {j\in 0,...,t-\Delta _ {active}} \Vert t _ {WC _ t}-t _ {WC _ j}\Vert \tag{9}\] 然后类似 Odometry 的过程，将当前帧的点云特征注册到 \(T _ {WC _ j ^ * }\) 的地图特征中。为了用 ICP 求解两者的相对位姿 \(T _ {C _ {j ^ * }C _ t}\)，初始化 \(T ^ {(0) } _ {C _ {j ^ * }C _ t}\) 为： \[\begin{align}
R _ {C _ {j^ * }C _ t} &= R ^ {-1} _ {WC _ {j ^ * }}R _ {WC _ t}\\
t _ {C _ {j^ * }C _ t} &= R ^ {-1} _ {WC _ {j ^ * }}(t _ {WC _ t}-t _ {WC _ {j ^ * }})\\
\end{align} \tag{10}\] 本文将 \(T ^ {(0) } _ {C _ {j ^ * }C _ t}\) 中的位移用 \(\lambda t _ {C _ {j ^ * }C _ t}\) 代替，其中 \(\lambda = \{0.0,0.5,1.0\}\)。由此可得到三种初始化后 ICP 迭代的结果，选择最合理的结果即可。
验证阶段，在 \(t + 1,...,t+ \Delta _ {verification}\) 时间段内，在 \(\mathcal{M} _ {active}\) 与 \(\mathcal{M} _ {inactive}\) 地图中分别作 Odometry 累加，查看两者的一致性，如果一致则认为该闭环检测是有效的。
2. SuMa++
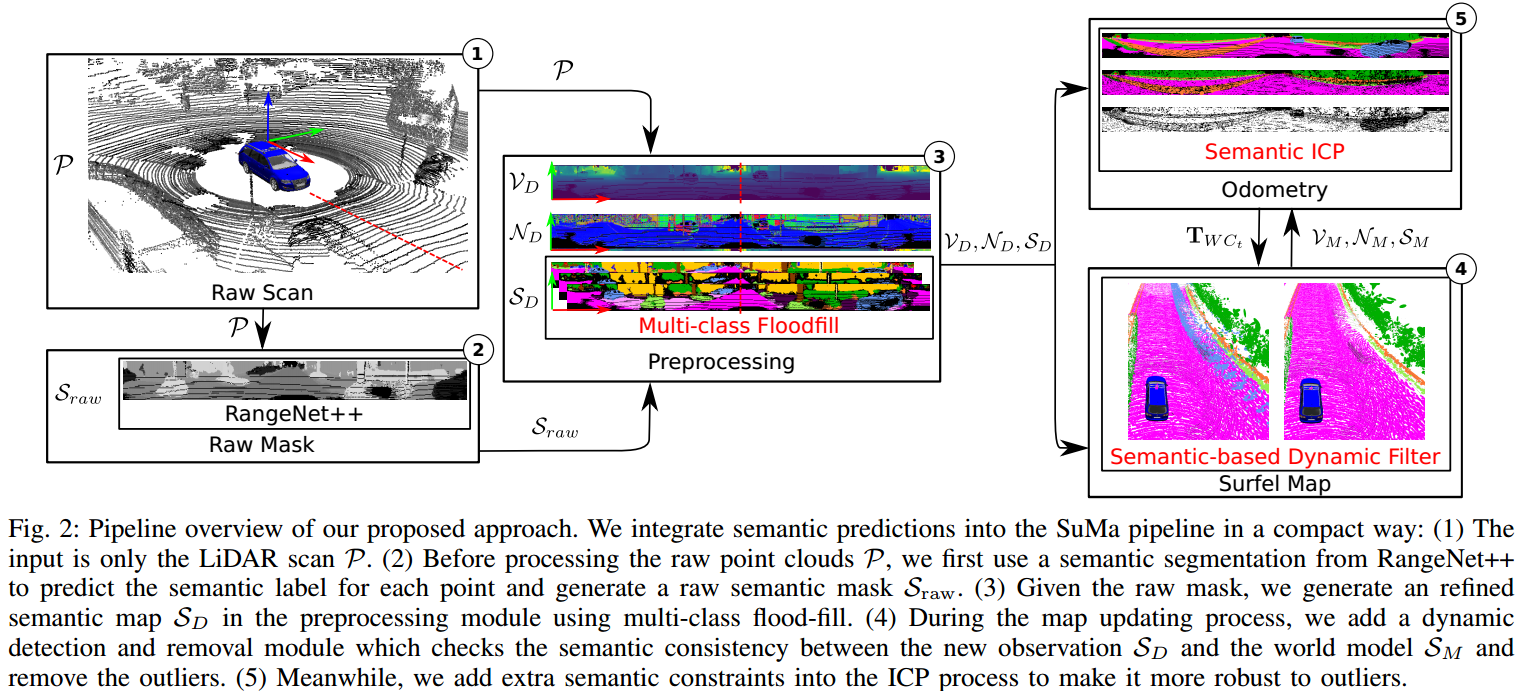SuMa++ 相比 SuMa，只增加了语义信息，算法框架没有改变。如图 3. 所示，SuMa++ 也有当前帧地图计算，当前地图计算，位姿计算，地图更新，闭环检测，闭环检测验证，位姿图优化等七个部分组成，其中，在地图计算中加入了有 RangeNet++ 产生的语义信息，在 \(\mathcal{V} _ D,\mathcal{N} _ D\) 的基础上，增加 \(\mathcal{S} _ D\) 特征；在地图更新中，根据语义信息加入了动态障碍物过滤的策略；在位姿计算中，用语义信息来权重化特征的 ICP 匹配迭代。
2.1. Semantic Map
RangeNet++ 也是基于式(2)投影试图下的分割模型，由此可得到 Surfel 特征图 \(\mathcal{V} _ D\) 中每个像素点的语义类别以及对应的类别概率。由于语义分割预测的噪声，本文用 Flood-fill 算法对网络输出的语义分割图 \(\mathcal{S} _ {raw}\) 作优化，得到顶点图对应的语义信息 \(\mathcal{S} _ D\)。 
考虑到语义分割在物体中心区域确定性较高，而在边缘处不确定性较高，所以 Flood-fill 算法采用两个步骤：
- 用腐蚀算法将与周围语义类别不一致的像素点移除，得到腐蚀后的语义图 \(\mathcal{S} _ {raw} ^ {eroded}\)；
- 结合有深度信息的顶点图 \(\mathcal{V} _ D\)，对腐蚀的边缘像素点填充为周围相近距离的顶点对应的语义类别，得到 \(\mathcal{S} _ D\)；
如图 4. 所示，该方法能修正边缘类别错误的情况。由此，\(\mathcal{V} _ D, \mathcal{N} _ D,\mathcal{S} _ D\)组成每一帧的特征点信息。
2.2. Filtering Dynamics
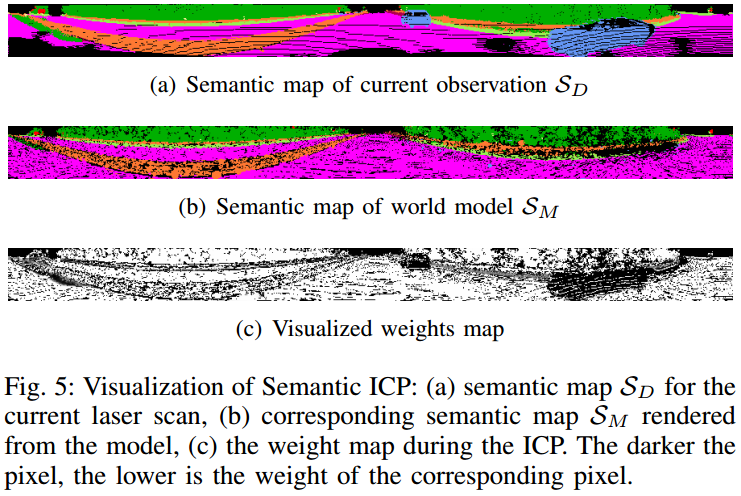
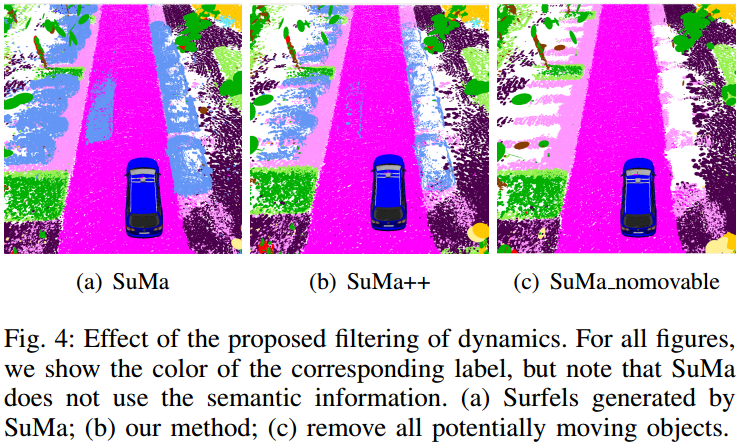有了语义类别信息后，在更新地图时，可计算当前帧每个 Surfel 与地图中对应 Surfel 的类别一致性，由此作为地图贝叶斯更新的惩罚项，如果类别不一致，地图中的 Surfel 稳定性概率会降低，直到去除。如图 5. 所示，这种方法能去除大部分动态障碍物区域所构成的 Surfel。地图具体的贝叶斯更新为： \[\begin{align}
l _ s ^ {(t)} = l _ s ^ {t-1} + \mathrm{odds}\left(p _ {stable}\cdot \mathrm{exp}\left(-\frac{\alpha ^ 2}{\sigma _ {\alpha} ^ 2}\right)\mathrm{exp}\left(-\frac{d ^ 2}{\sigma _ d ^ 2}\right)\right) - \mathrm{odds}(p _ {prior}) - \mathrm{odds}(p _ {penalty})
\end{align} \tag{11}\]
2.3. Semantic ICP
在式(5)的 ICP 误差项基础上，可加入语义约束，对误差项作权重化： \[ E(\mathcal{V} _ D,\mathcal{V} _ M, \mathcal{N} _ M) = \sum _ {u\in\mathcal{V} _ D}w _ u n _ u ^ T\cdot\left(T _ {C _ {t-1}\;C _ t}^{(k)}\;u-v _ u\right) ^ 2 \tag{12}\] 其中权重项结合了语义约束与几何约束，以此来减少离群特征点对优化的影响： \[w _ u ^{(k)} = \rho _ {Huper}\left(r _ u ^ {(k)}C _ {semantic}(\mathcal{S} _ D(u),\mathcal{S} _ M(u))\right)\mathbb{1}\left\{l _ s ^ {(k)}\geq l _ {stable}\right\} \tag{13}\] 其中 \(\rho _ {Huber}(r)\) 是 Huber 核函数： \[\rho _ {Huber}(r)=\left\{\begin{array}{l} 1 &,\mathrm{if}\;\vert r\vert < \sigma\\ \sigma\vert r\vert ^ {-1} &,\mathrm{otherwise} \end{array}\tag{14}\right.\] 语义约束项为： \[C _ {semantic}\left((y _ u,P _ u),(y _ {v _ u}, P _ {v _ u})\right)=\left\{\begin{array}{l} P(y _ u|u) &,\mathrm{if}\;y _ u=y _ {v _ u}\\ 1-P(y _ u|u) &,\mathrm{otherwise} \end{array}\tag{15}\right.\]
如图 6. 所示，在语义信息的约束下，如果当前帧某个 Surfel 的类别与地图中对应的 Surfel 类别不一致，那么就会减少该 Surfel 匹配对的误差项。
3. Thinkings
利用检测或分割得到的语义信息去过滤当前帧以及地图中的动态障碍物，在 SLAM/Odometry 中已经非常常见，其实可以大概率相信语义信息，然后直接将对应的点云干掉。而本文以融合迭代的思路，想通过将信将疑的方式来完成有效的 ICP 匹配（既要滤掉大多数动态障碍物的影响，也期望一堆车停在场景中时然后保留足够匹配的特征点）。但是一般工程上，直接干掉也够用，毕竟场景够大，不太可能出现特征点不够匹配的情景。而本方法的高效性在于，寻找当前帧与地图中的 Surfel 匹配时，直接采用图像索引然后顶点图距离及法向量图角度判断有效性的形式，没有 KD-Tree，极大提高效率，类似 ICPCUDA[4]。
4. Reference
[1] Behley, Jens, and Cyrill Stachniss. "Efficient Surfel-Based SLAM using 3D Laser Range Data in Urban Environments." Robotics: Science and Systems. 2018.
[2] Chen, Xieyuanli, et al. "Suma++: Efficient lidar-based semantic slam." 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2019.
[3] Milioto, Andres, et al. "RangeNet++: Fast and accurate LiDAR semantic segmentation." 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2019.
[4] https://github.com/mp3guy/ICPCUDA
