基于 Attention 的 Transformer 已经从 NLP 领域逐渐要统治图像，点云领域，本文详述了其原理机制，以及在图像，点云中的一些应用。
1. Attention to Transformer[1]
1.1. Attention
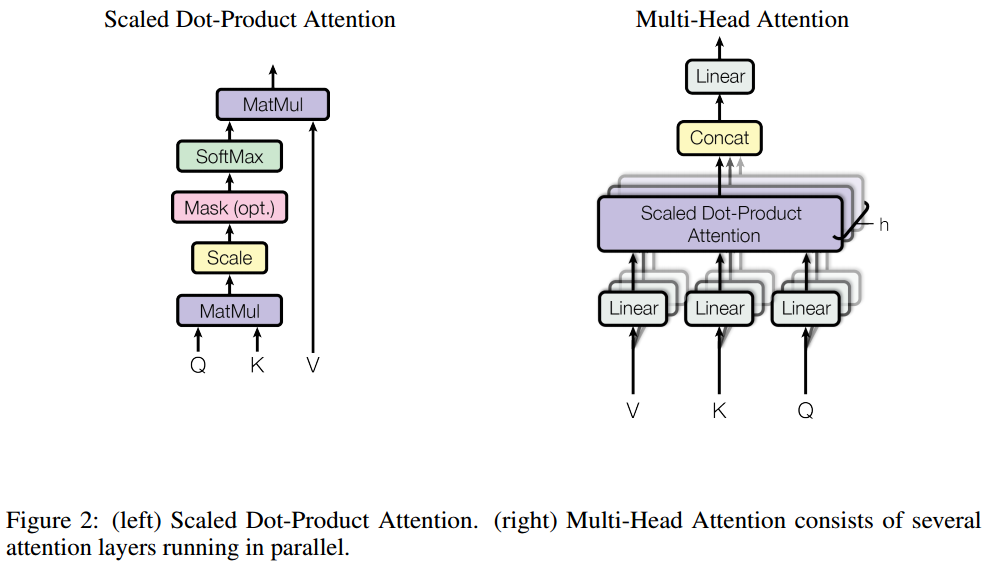
Attention 的机制在于能自动关注到输入序列中的重要部分。如图 1. 左图，设输入 query \(Q\in\mathbb{R} ^ {N\times d _ k}\)，key-value \(K\in\mathbb{R} ^ {N _ k\times d _ k}, V\in\mathbb{R} ^ {N _ k\times d _ v}\)，那么 Attention 映射方程 \(\mathcal{A}(\cdot)\) 将其映射为输出 \(\mathbb{R} ^ {N\times d _ k}\)。具体的： \[\begin{align} \mathcal{A}(Q,K,V) &= \mathrm{score}(Q,K)V \\ &= \mathrm{softmax}\left(\frac{QK ^ T}{\sqrt{d _ k}}\right)V \end{align} \tag{1}\] 当 \(d _ k\) 较大时，\(QK ^ T\) 的幅值会较大，导致 softmax 的反传梯度会趋于很小，为了降低这种影响，引入尺度变换 \(\frac{1}{\sqrt{d _ k}}\)。以上矩阵运算的维度变化为： \[\begin{align} \mathrm{score}(\cdot):&\;\; \mathbb{R} ^ {N\times d _ q}, \mathbb{R} ^ {N _ k\times d _ k} \rightarrow \mathbb{R} ^ {N\times N _ k}，其中\; d _ k=d _ q=d _ m\\ \mathcal{A}(Q,K,V):&\;\; \mathbb{R} ^ {N\times d _ k}, \mathbb{R} ^ {N _ k\times d _ k}, \mathbb{R} ^ {N _ k\times d _ v} \rightarrow \mathbb{R} ^ {N\times d _ k} \end{align} \tag{2}\] 如图 1. 右图，实践中，采用 MultiHead Attention 形式，在不同的子空间不同的位置编码中学习特征，然后再作整合： \[ \mathrm{MultiHead(Q,K,V)} =\mathrm{Concat(head _ 1,..., head _ h)}W ^ o \tag{3}\] 其中 \(\mathrm{head _ i} = \mathcal{A}(QW _ i ^ Q,KW _ i ^ K,VW _ i ^ V)\)，参数 \(W _ i ^ Q\in\mathbb{R} ^ {d _ m\times d _ k},W _ i ^ K\in\mathbb{R} ^ {d _ m\times d _ k},W _ i ^ V\in\mathbb{R} ^ {d _ m\times d _ v}\)；\(W ^ o\in\mathbb{R} ^ {hd _ v\times d _ m}\)，为了与 Attention 计算复杂度类似，令 \(d _ k=d _ v=d _ m/h\)。
1.2. Transformer
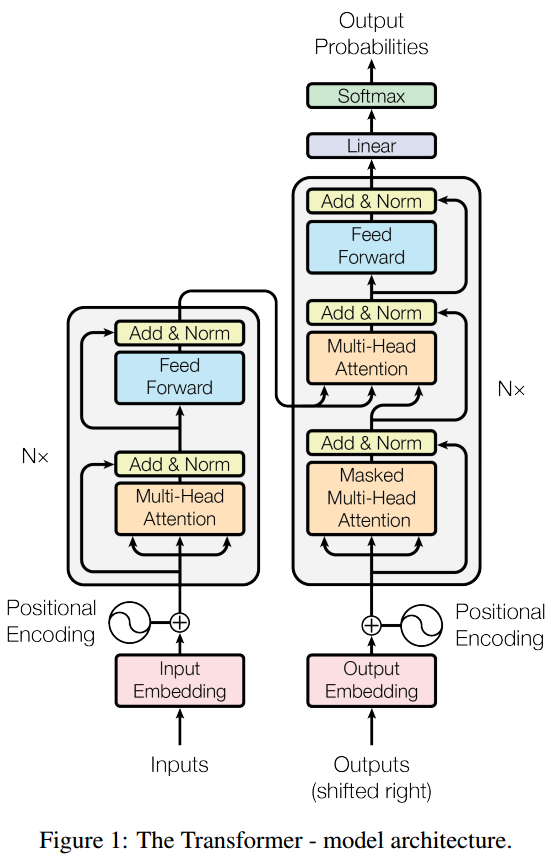
如图 2. 所示，Transformer 结构有 Encoder，Decoder 构成，基本层由 Multi-head Attention 和 point-wise Fully Connected Layer 构成，称之为 Multi-head Attention： \[\begin{align} \mathcal{A} ^ {MH}(X,Y)=\mathrm{LayerNorm}(S + \mathrm{rFF}(S)) \\ S = \mathrm{LayerNorm}(X+\mathrm{Multihead(X,Y,Y)}) \end{align} \tag{4}\] 其中 \(\mathrm{rFF}\) 表示 row-wise fead-forward network。N 个该基础层叠加组成 Encoder 网络，其维度变换为： \[\mathcal{A} ^ {MH}:\; \mathbb{R} ^ {N\times d _ m}, \mathbb{R} ^ {N _ k\times d _ m} \rightarrow \mathbb{R} ^ {N\times d _ m} \tag{5}\]
1.3. Positional Encoding
由于 Transformer 对输入没有提取序列信息的能力，所以需要对输入作位置编码。位置编码可以通过学习得到，也可以用函数编码： \[\begin{align} PE _ {pos,2i} &= sin(pos/10000 ^ {2i/d _ {model}}) \\ PE _ {pos,2i+1} &= cos(pos/10000 ^ {2i/d _ {model}}) \end{align} \tag{6}\]
其中 pos 表示位置，i 表示特征维度。
1.4. Why Self-Attention
如图 3. 所示，Attention 相比 Recurrent，Convolution，其在计算复杂度，并行化，输入序列间的最大距离上有较好的优势。
2. Vision Transformer[2]
如图 4. 所示，首先将图像 \(\mathbf{x}\in\mathbb{R} ^ {H\times W\times C}\) 变换成 patch 序列 \(\mathbf{x} _ p\in\mathbb{R} ^ {N\times (P ^ 2\cdot C)}\)，其中 \((P,P)\) 是 patch 尺寸，\(N=HW/P ^ 2\)。然后用线性变换 \(\mathbf{E}\in\mathbb{R} ^ {(P ^ 2\cdot C)\times D}\) 将每个 patch 的特征维度映射到 D 维。最终的 Transformer 数学形式为： \[\begin{align}
\mathbf{z} _ 0 &=[\mathbf{x} _ {class};\;\mathbf{x} _ p^1\mathbf{E};\;\mathbf{x} _ p^2\mathbf{E};\;\cdots;\;\mathbf{x} _ p^N\mathbf{E}]+\mathbf{E} _ {pos}, \;\;& \mathbf{E}\in\mathbb{R} ^ {(P^2\cdot C)\times D},\;\mathbf{E} _ {pos}\in\mathbb{R} ^ {(N+1)\times D}\\
\mathbf{z} _ l' &= \mathrm{MultiHeadAttention(LN(}\mathbf{z} _ {l-1}))+\mathbf{z} _ {l-1}, \;\;& l=1\cdots L\\
\mathbf{z} _ l &= \mathrm{MLP(LN(}\mathbf{z})) _ l'+\mathbf{z} _ l', \;\;& l=1\cdots L\\
\mathbf{y} &= \mathrm{LN}(\mathbf{z}) _ L ^0\\
\end{align} \tag{7}\] 这里的关键是，在输入序列中串联了分类结果 \(\mathbf{z} _ 0 ^ 0= \mathbf{x} _ {class}\)，经过 \(L\) 次查询迭代后，获得最终的分类结果 \(\mathbf{z} _ L ^ 0\)。
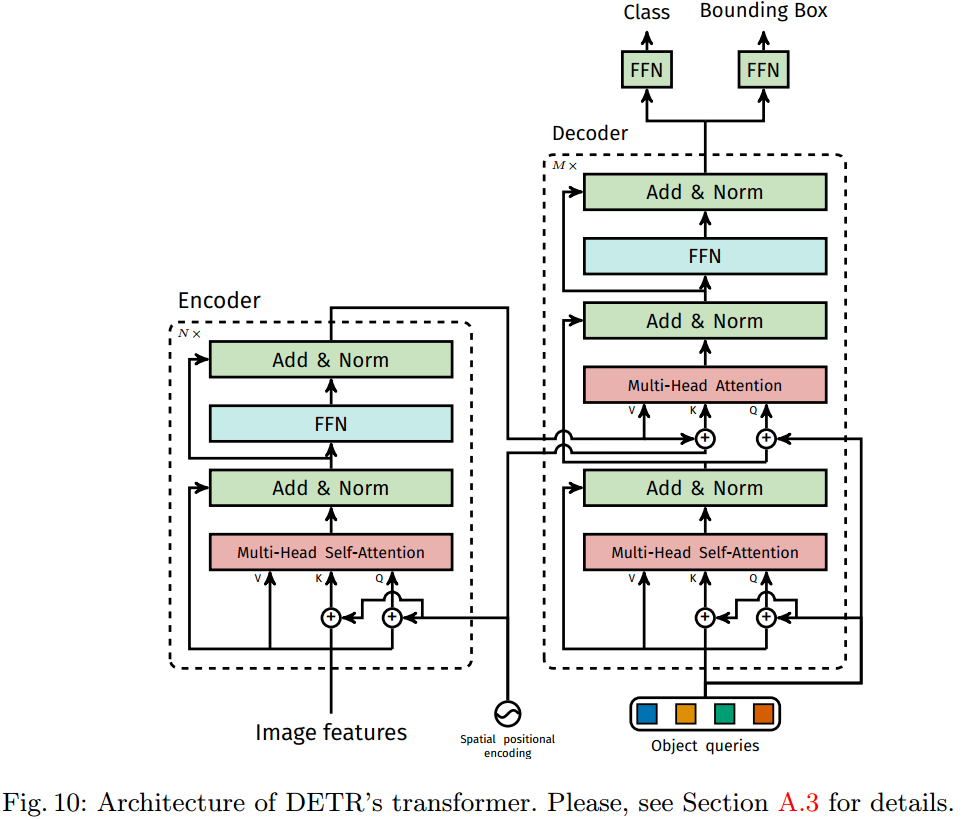
3. DETR[3]
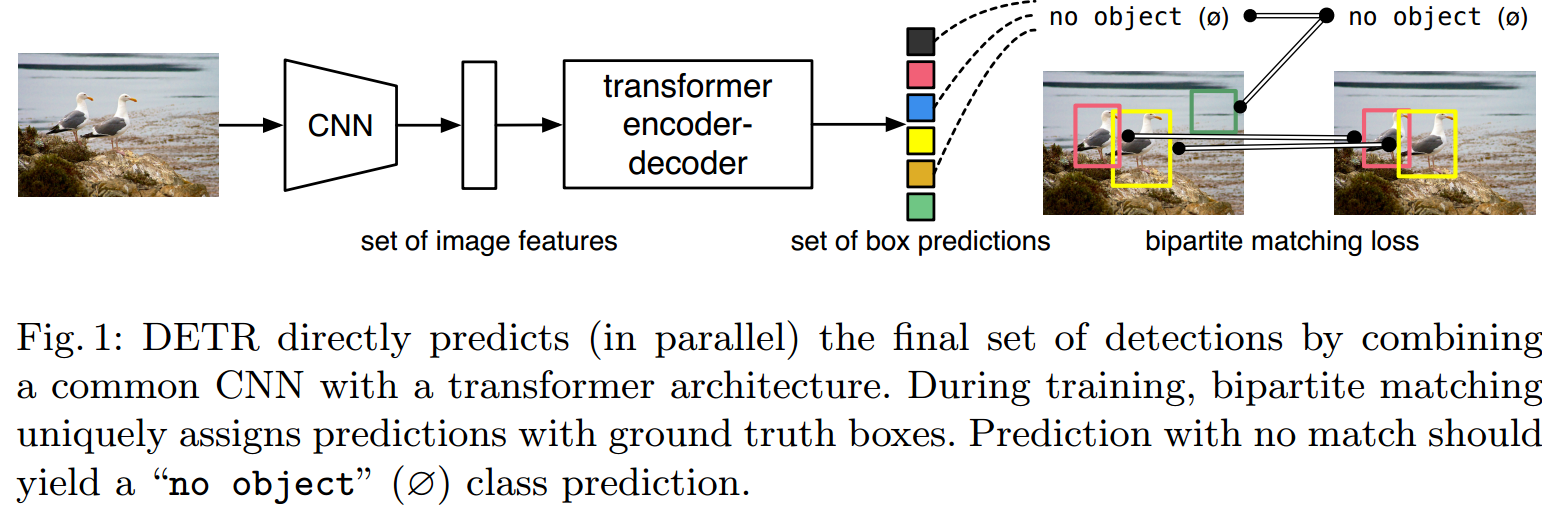
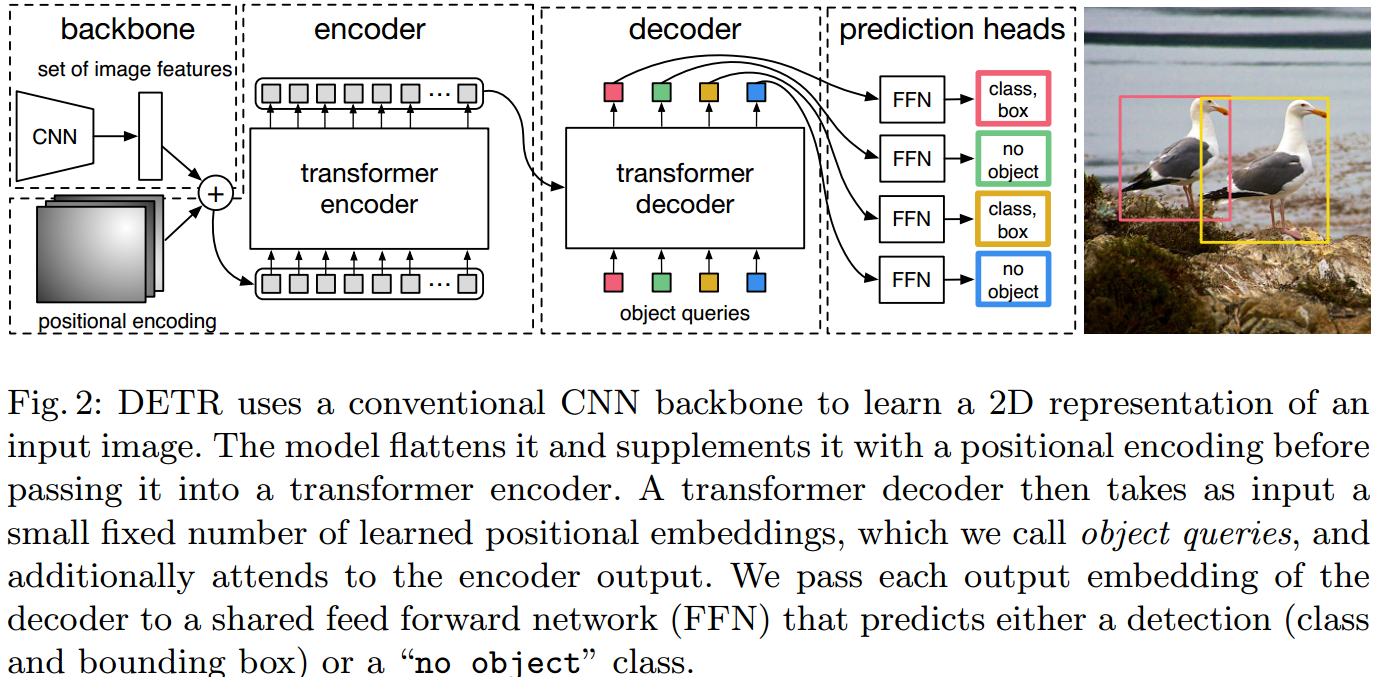如图 5.6. 所示，DETR 首先用 CNN 网络作图像特征提取，然后用 Transformer Encoder 作特征序列化融合，接着用 Transformer Decoder 作目标框查询，得到检测结果。
