If you don’t know the measurement uncertainty, don’t make the measurement at all![1]
Uncertainty 在自动驾驶测量中的重要性在之前的文章，如 Perception Uncertainty in Deep Learning 中已经有较详细的阐述，这里不做赘述。但更重要的是，如何确保 Uncertainty 估计的准确性。如图 1. 所示，本文讨论如何评估 Uncertainty 估计的准确性，以及通过 Uncertainty Calibration 来修正其估计误差。
1. Uncertainty Estimation for Object Detection
以目标检测任务为例，深度学习中的 Uncertainty 估计可分为两大类方法：Ensemble Approach，以及 Direct-modeling Approach。本文以 Direct-modeling 方法为例，假设网络输出符合多多变量高斯分布。对于 Anchor-Free 的 3D 目标检测，分类的预测量为目标类别分数 \(p(y _ c=1|) = s _ {\mathbf{x}}\)，回归预测量为： \[\mathbf{u _ x} = [\mathrm{cos}(\theta), \mathrm{sin}(\theta), dx,dy,\mathrm{log}(l),\mathrm{log}(w)] \tag{1}\] 假设回归输出量符合多变量独立高斯分布 \(p(\mathbf{y _ r}| \mathbf{x})=(\mathbf{u _ x,\Sigma _ x})\)，那么其协方差矩阵为对角矩阵： \[\mathbf{\sigma _ x} ^ 2=[\sigma ^2 _ {\mathrm{cos}(\theta)}, \sigma ^2 _ {\mathrm{sin}(\theta)}, \sigma ^ 2 _ {dx}, \sigma ^ 2 _ {dy}, \sigma ^ 2 _ {\mathrm{log}(l)}, \sigma ^ 2 _ {\mathrm{log}(w)}] _ {\mathbf{x}} \tag{2}\] 由此加入预测的 Uncertainty 分支，Loss 项为： \[L _ {reg}=\frac{1}{2}(\mathbf{y _ r-u _ x})\mathrm{diag}(\frac{1}{\mathbf{\sigma ^ 2 _ x}})(\mathbf{y _ r-u _ x}) ^ T+\frac{1}{2}\mathrm{log}(\mathbf{\sigma ^ 2 _ x})\mathbf{1} ^ T \tag{3}\]
2. Uncertainty Evaluation
对于数据集 \(\{(\mathbf{x} ^ n,y _ c ^ n,\mathbf{y} _ r ^ n)\} _ {n=1} ^ N\)，\(\mathbf{X}\) 表示输入数据，\(\mathbf{Y} _ c\) 表示分类标签，\(\mathbf{Y _ r}\) 表示回归标签。概率描述为：\(\mathbf{X, Y} _ c \sim \mathbb{P} _ c\)，以及 \(\mathbf{X,Y _ r}\sim\mathbb{P} _ r\)。对于分类问题，，softmax score 预测了目标分类的概率分布，即 \(\mathbf{F} _ c ^ n(y _ c=1)=p(y _ c=1|\mathbf{x} ^ n)=s _ {\mathbf{x} ^ n}\)。对于回归问题，网络预测了概率密度函数 PDF：\(p(\mathbf{y _ r} ^ n | \mathbf{x} ^ n) = \mathcal{N}(\mathbf{u _ {x ^ n},\Sigma _ {x ^ n}})\)，其累积概率分布函数 CDF 定义为 \(\mathbf{F} _ r ^ n(\mathbf{y} _ r)\)，反函数为 \(\mathbf{F} _ r ^ {n ^ {-1}}(p)\)。
准确的不确定性预测意味着，预测的概率近似等于统计的频率。具体的：
分类问题
0.9 的分数意味着 90% 的物体是被分类准确的。对于 \(\forall p\in[0,1]\)，数学形式为： \[\mathbb{P} _ c(\mathbf{Y} _ c=1|\mathbf{F} _ c(\mathbf{Y} _ c=1)=p)\approx \frac{\sum _ {n=1} ^ N\mathbb{1}(y _ c ^ n=1,F _ c ^ n(y _ c=1)=p)}{\sum _ {n=1} ^ N\mathbb{1}(F _ c ^ n(y _ c=1)=p)} \tag{4}\]回归问题
对于预测物体，其 90% 置信空间内，90% 的真值物体应该在置信空间内。对于 \(\forall p\in[0,1]\)，数学形式为： \[\mathbb{P} _ r(\mathbf{Y} _ r\leq\mathbf{F} _ r ^ {-1}(p))\approx\frac{\sum _ {n=1} ^ N\mathbb{1}(y _ r ^ n\leq F _ r ^{n ^ {-1}}(p))}{N} \tag{5}\]
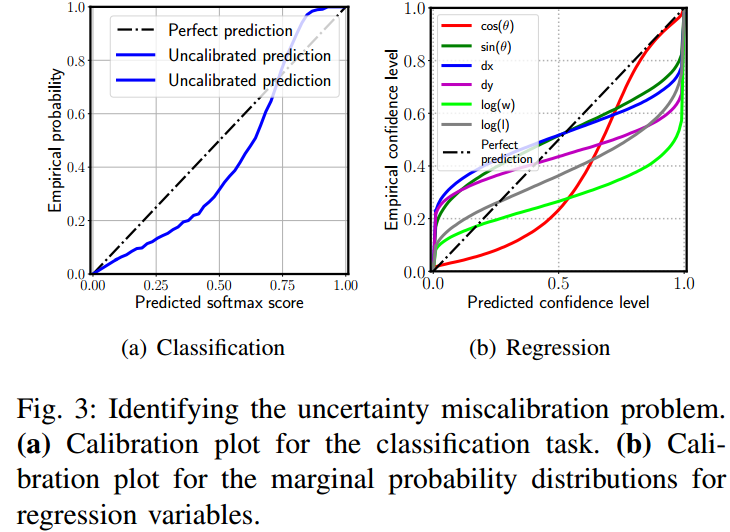由此可用 calibration plot 来刻画不确定性估计的准确性。如图 2. 所示，横坐标表示预测的概率，纵坐标表示统计的概率，将概率值划分为 \(0 < p _ c ^ 1 < ... < p _ c ^ m < ... < 1\) 个置信区域，理想的 Calibration Plot 是对角线。计算该对角线与实际曲线的 Expected Calibration Error(ECE) 即可作为评估 Uncertainty 估计的准确性： \[\mathrm{ECE} =\sum _ {m=1} ^ M\frac{N _ m}{N}\vert p ^ m-\hat{p} ^ m\vert\tag{6}\]
3. Uncertainty Recalibration
为了使得 Calibration Plot 能完美贴合对角线，需要对 Uncertainty 进行标定。
3.1. Isotonic Regression
对于预测的累积概率分布函数 \(p=\mathbf{F} _ r(y _ r)\)，预测一个额外模型 \(g(p)\) 使得满足式 (5) 条件，该映射模型函数是非参单调递增的。额外模型通过 validation 数据集训练得到。
3.2. Temperature Scaling
对式 (2) 中的各方差作 \(T > 0\) 的尺度变换：\(\hat{\sigma}\leftarrow\sigma ^ 2/T \)。最优的 \(T\) 通过最大化 Negative Log Likelihood(NLL) 实现，等价于最小化式 (3) 的 Loss 项。
3.3. Calibration Loss
由式 (3) 可知，Variance 的预测是通过无监督的形式隐式来预测的，所以本质上就无法保证 Variance 的绝对正确性，所以可加入监督项来保证其正确性。因为一个准确的 Uncertainty 意味着预测的 Variance 与预测量和真值量的 Variance 是一致的，所以设计 calibration loss： \[ L _ {calib} =\Vert \mathbf{\sigma _ x} ^ 2-(\mathbf{y _ r-u _ x})\odot (\mathbf{y _ r-u _ x})\Vert\tag{7}\] 最终的 Loss 为： \[L _ {total} = L _ {reg}+\lambda L _ {calib}\tag{8}\]
4. Recalibration Results
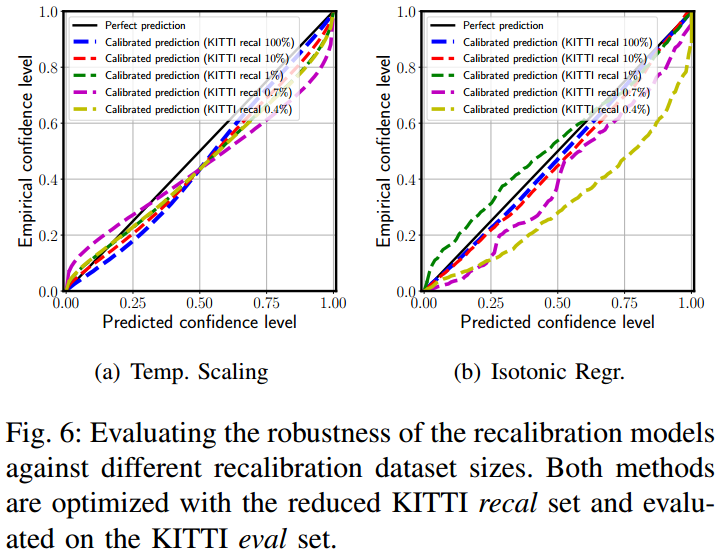如图 3. 所示，经过标定后，预测的概率分布接近于实际统计分布。
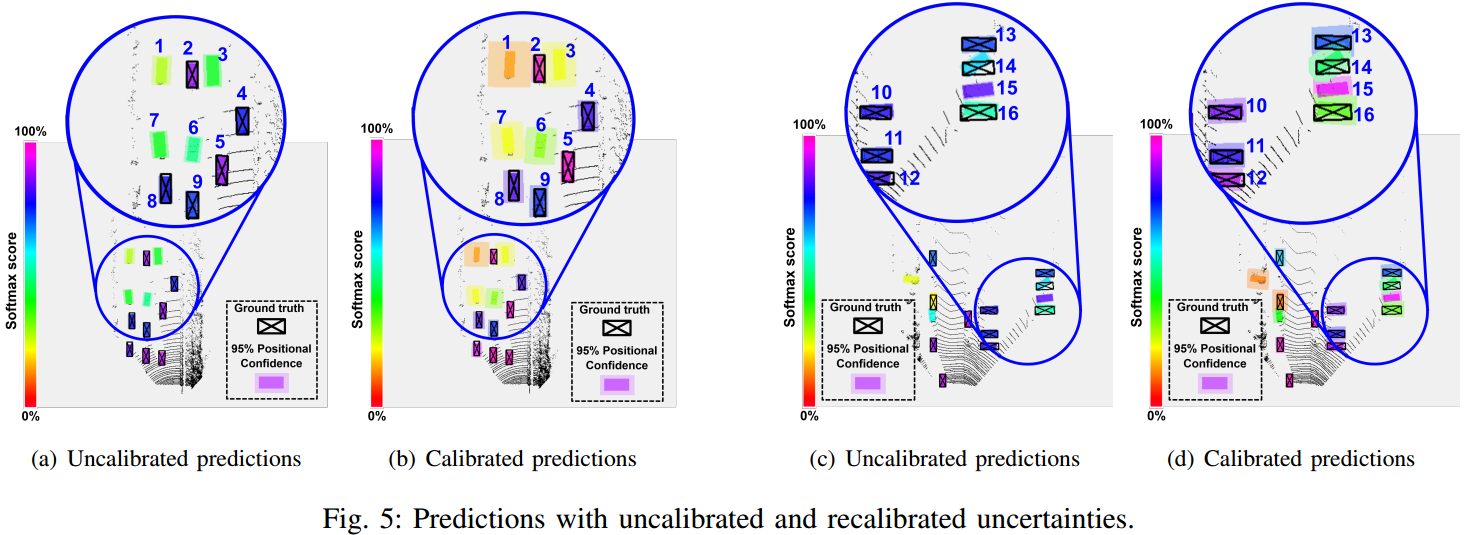图 4. 可视化了标定前后 Uncertainty 的准确程度，可见标定后，越是遮挡的目标，Uncertainty 越大，符合预期。此外，标定后目标检测的精度也有较大的提升。
5. Reference
[1] Feng, Di, et al. "Can we trust you? on calibration of a probabilistic object detector for autonomous driving." arXiv preprint arXiv:1909.12358 (2019).
[2] Kuleshov, Volodymyr, Nathan Fenner, and Stefano Ermon. "Accurate uncertainties for deep learning using calibrated regression." arXiv preprint arXiv:1807.00263 (2018).
