VLOAM(Visual-lidar Odometry and Mapping)

　　LOAM 中 Lidar Odometry 模块将当前累积的 Sweep 点云通过 Sweep-to-Sweep 注册到上一时刻的 Sweep 点云，从而生成高频低精度的位姿；Lidar Mapping 则将完整的当前 Sweep 点云通过 Sweep-to-Model 注册到全局地图中，从而生成低频高精度的位姿。这其中高频低精度的位姿可通过其它方式获得，如 IMU 等其它高频传感器。本文^[1] 采用高频的 Visual Odometry 来生成高频低精度的位姿，低频高精度的位姿则还是通过 Lidar Odometry(Mapping) 获得，但做了细微的改变。 　　如图 1. 所示，VSLAM 结合了高频低精度的 Visual Odometry，以及低频高精度的 Lidar Odometry，最终得到高频高精度的位姿，以及准确的全局点云地图。

1. Framework

　　本文坐标系以相机坐标系 \(\{S\}\) 为主(x left，y upward，z forward)，所有点云都会通过外参转换到该坐标系下；设世界坐标系 \(\{W\}\) 为起始点。那么位姿求解问题的数学描述为：给定各个坐标系 \(\{S\}\) 下的图像和点云，求解所有 \(\{S\}\) 在 \(\{W\}\) 下的表示，以及 \(\{W\}\) 下地图的构建。 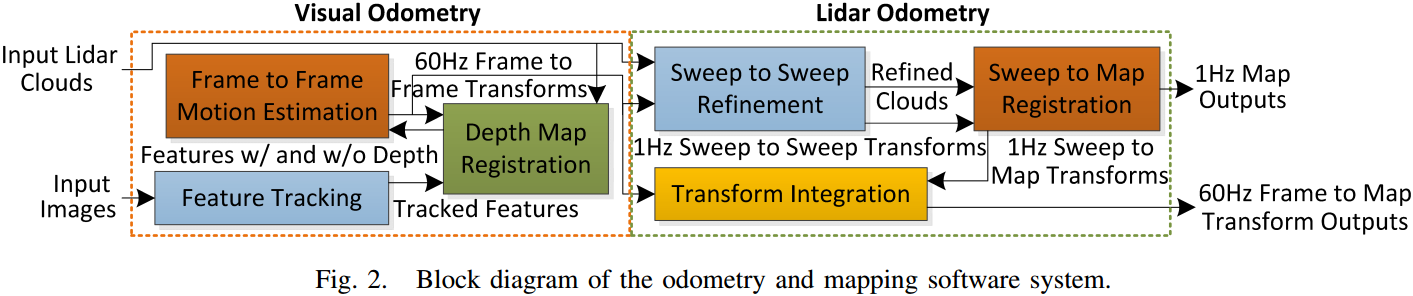　　如图 2. 所示，Visual Odometry 作前后帧的特征跟踪(或匹配)，结合点云深度信息，作 Frame-to-Frame 的运动位姿估计；Lidar Odometry 则先通过 Sweep-to-Sweep 作运动粗估计，然后用 Sweep-to-Map 作精估计(其中 Sweep 的定义可见 LOAM)。由此输出低频的全局地图，以及高频的位姿估计。

2. Visual Odometry

　　首先用 Visual Odometry 得到的高频位姿估计将点云注册为一个局部的深度图。由此维护三种类型的特征点：1. 从深度图获得深度的特征点；2. 从前后帧三角化获得深度的特征点；3. 没有深度的特征点。这里的特征点提取可采用任意的特征点提取方法，如果采用前后帧特征匹配的策略，则还得作相应的特征描述子提取，如果采用特征跟踪策略，则不需要。
　　设图像帧序号 \(k\in Z ^ +\)，特征点序号 \(i\in\mathcal{I}\)，那么在相机坐标系 \(\{S ^ k\}\) 下，特征点坐标表示为 \(\sideset{^S}{}X ^ k _ i = [\sideset{^S}{}x ^ k _ i,\sideset{^S}{}y ^ k _ i,\sideset{^S}{}z ^ k _ i] ^ T\)，其归一化表示为 \({\sideset{^S}{}{\overline{X}}} ^ k _ i = [\sideset{^S}{}{\overline{x}} ^ k _ i,\sideset{^S}{}{\overline{y}} ^ k _ i,\sideset{^S}{}{\overline{z}} ^ k _ i] ^ T\)。前后匹配的特征点与运动位姿的关系为： \[{\sideset{^S}{}X} ^ k _ i=R\;{\sideset{^S}{}X} ^ {k-1} _ i+T \tag{1}\] 其中 \({\sideset{^S}{}X} ^ k _ i\) 为当前帧的特征点坐标，由于还未估计出当前帧的位姿，所以该特征点是没有深度信息的。根据特征点 \({\sideset{^S}{}X} ^ {k-1} _ i\) 是否有深度信息，可归纳出方程：

1. \({\sideset{^S}{}X} ^ {k-1} _ i\) 有深度信息 \[\begin{align} &{\sideset{^S}{}{\overline{d}}} ^ k _ i{\sideset{^S}{}{\overline{X}}} ^ k _ i=R\;{\sideset{^S}{}X} ^ {k-1} _ i+T\\ \Longrightarrow & \left\{\begin{array}{l} \left({\sideset{^S}{}{\overline{z}}} ^ k _ i R _ 1-{\sideset{^S}{}{\overline{x}}} ^ k _ i R _ 3\right){\sideset{^S}{}{X}} ^ k _ i + {\sideset{^S}{}{\overline{z}}} ^ k _ i T _ 1-{\sideset{^S}{}{\overline{x}}} ^ k _ i T _ 3 = 0\\ \left({\sideset{^S}{}{\overline{z}}} ^ k _ i R _ 2-{\sideset{^S}{}{\overline{y}}} ^ k _ i R _ 3\right){\sideset{^S}{}{X}} ^ k _ i + {\sideset{^S}{}{\overline{z}}} ^ k _ i T _ 2-{\sideset{^S}{}{\overline{y}}} ^ k _ i T _ 3 = 0\\ \end{array}\tag{2}\right. \end{align}\] 其中 \(\sideset{^S}{}{d} ^ k _ i = \left\Vert \sideset{^S}{}{\overline{X}} ^ k _ i\right\Vert \)，\(R _ l, T _ l\) 为第 \(l\in\{1,2,3\}\) 行的 \(R,T\)。
2. \({\sideset{^S}{}X} ^ {k-1} _ i\) 无深度信息 \[\begin{align} &{\sideset{^S}{}{\overline{d}}} ^ k _ i{\sideset{^S}{}{\overline{X}}} ^ k _ i=R\;{\sideset{^S}{}{\overline{d}}} ^ {k-1} _ i\;{\sideset{^S}{}X} ^ {k-1} _ i+T\\ \Longrightarrow & \begin{bmatrix} -{\sideset{^S}{}{\overline{y}}} ^ k _ i T _ 3 +{\sideset{^S}{}{\overline{z}}} ^ k _ i T _ 2 &{\sideset{^S}{}{\overline{x}}} ^ k _ i T _ 3-{\sideset{^S}{}{\overline{z}}} ^ k _ i T _ 1 &-{\sideset{^S}{}{\overline{x}}} ^ k _ i T _ 2+{\sideset{^S}{}{\overline{y}}} ^ k _ i T _ 1 \end{bmatrix} R\;{\sideset{^S}{}{\overline{X}}} ^ {k-1} _ i = 0 \tag{3} \end{align}\] 推导过程比较繁杂，但是也比较简单，依次消去 \(\sideset{^S}{}{d} ^ k _ i,\sideset{^S}{}{d} ^ {k-1} _ i\) 即可。

将所有特征点所构成的 residual 累积，然后可用 LM 法求解该非线性问题中 6-DOF 的位姿。考虑到有较大 residual 的特征点大概率是离群点，所以对特征点的 residual 作权重处理，residual 越大，权重越小。
　　为了获取特征点的深度，维护一个从点云中采样的在上一帧图像坐标系下的深度图，深度图维护较新的点云深度信息，并且保持一定的点密度。深度图中的点用极坐标形式的 2D KD-tree 存储，具体的特征点深度值计算通过周围深度点构成的平面插值得到。在无法从深度图中获得特征点的深度信息时，如果特征点被跟踪了较长的距离，那么采用三角测量法获得该特征点深度。三种点的可视化如图 3. 所示。

3. Lidar Odometry

　　高频的 frame-to-frame Visual Odometry 得到的位姿估计是粗糙且有漂移的，接下来用 Lidar Odometry 作进一步的精估计。激光雷达里程计又基于 coarse-to-fine 的思想，分为 sweep-to-sweep 以及 sweep-to-map 两个步骤。这两个步骤的具体计算过程很相似，只不过前者是前后帧点云的匹配以消除运动引入的点云畸变，后者则是当前帧去畸变的点云与世界坐标系下的地图点云匹配，能消除累积误差。总体上这部分与 LOAM 处理方式一致。

3.1. Sweep-to-Sweep

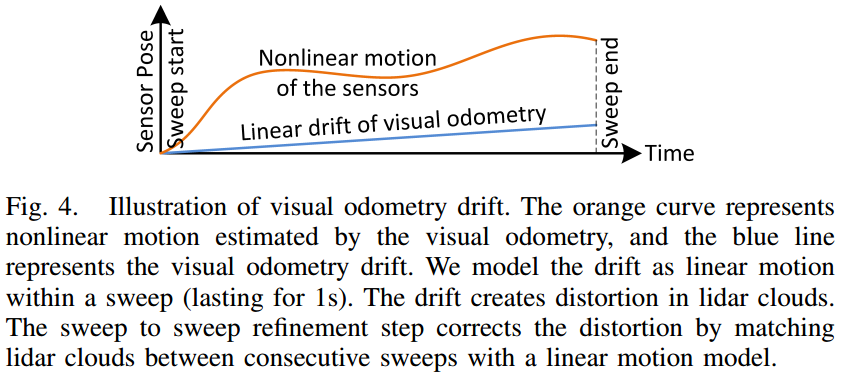　　与 LOAM 一样，对第 \(m\in Z ^ +\) 个 Sweep 点云 \(\mathcal{P} ^ m\)，提取线特征 \(\mathcal{E} ^ m\) 与面特征 \(\mathcal{H} ^ m\)。如图 4. 所示，将 Visual Odometry 产生的漂移建模为线性运动模型。假设第 \(m\) 个 Sweep 扫描期间其漂移的位姿为 \(T'\in\mathbb{R} ^ {6\times 1}\)，那么，对于点 \(i\in\mathcal{E} ^ m\cup\mathcal{H} ^ m\)，其接收时间 \(t _ i\) 对应的位姿漂移为： \[T _ i' = T'(t _ i-t ^ m)/(t ^ {m+1}-t ^ m) \tag{4}\] 　　为了求解 \(T'\)，分别找到当前帧特征点 \(\mathcal{E} ^ m,\mathcal{H} ^ m\) 与上一帧特征点的匹配，然后计算距离误差的 residual，累积后即可用 LM 法来求解该非线性最小二乘问题。对于 \(\mathcal{E} ^ m\)，在 \(\mathcal{P} ^ {m-1}\) 中找到最近的两个线特征点，从而计算 point-to-edge 距离；对于 \(\mathcal{H} ^ m\)，在 \(\mathcal{P} ^ {m-1}\) 中找到最近的三个面特征点，从而计算 point-to-plane 距离。找特征点的过程通过 3D KD-tree 实现(工程上为了加速，可以采用其它方法)。由此得到一系列方程： \[f({\sideset{^S}{}X} ^ m _ i, T _ i')=d _ i \tag{5}\] 其中 \({\sideset{^S}{}X} ^ m _ i\) 是点 \(i\in\mathcal{E} ^ m\cup\mathcal{H} ^ m\) 在 \(\{S ^ m\}\) 下的坐标。计算 \(T'\) 后，即可得到去畸变的当前帧点云 \(\mathcal{P} ^ m\)。

3.2. Sweep-to-Map

　　去畸变的点云 \(\mathcal{P} ^ m\) 可以进一步注册到点云地图 \(\mathcal{Q} ^ {m-1}\) 中。考虑到点云地图较为稠密，匹配过程为计算局部点集的分布特征值与特征向量。特征值一大两小，即为线特征；特征值两大一小则为面特征。因为没有 Sweep-to-Sweep 中的运动模型，所以可直接用 ICP 方法来优化求解位姿。最终得到低频高精度的位姿结果。

4. Reference

[1] Zhang, Ji, and Sanjiv Singh. "Visual-lidar odometry and mapping: Low-drift, robust, and fast." 2015 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2015.