车道线检测(Lane Detection)是 ADAS 系统中重要的功能模块，而对于 L4 自动驾驶系统来说，在不完全依赖高精度地图的情况下，车道线检测结果也是车辆运动规划的重要输入信息。由于俯视图(BEV, Bird's Eye View)下做车道线检测相比于前视图，有天然的优势，所以本文根据几篇论文(就看了两三篇)及项目经验，探讨总结俯视图下做车道线检测的流程方案，并主要介绍 IPM 逆透视变换原理，[0]为车道线检测资源集。
1. 流程框架
由于激光点云的稀疏性，目前车道线检测主要还是依靠图像，激光点云数据当然可作为辅助输入。由此归纳一种可能的粒度较粗的俯视图下车道线检测的流程：
- IPM 逆透视变换，将图像前视图变换为俯视图；
- 网络，提取特征，进行像素级别的分类或回归；
- 后处理，根据网络输出作相应后处理，网络输出可能是像素级别预测；
网络相对比较成熟，后处理则在不同网络方法下复杂度差异很大，这里不做讨论。接下来主要讨论如何进行逆透视变换。
2. IPM 逆透视变换
设变换前后图像坐标为 \((u,v)\), \((u',v')\), 对于仿射变换(Affine transformation)，变换前后保持了线的平行性，其变换矩阵 A： \[\begin{bmatrix} u' \\ v' \\ \end{bmatrix} = A \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} a_{11} &a_{12} &a_{13} \\ a_{21} &a_{22} &a_{23} \end{bmatrix} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} \tag{1}\] 对透视变换，可表示为： \[\begin{bmatrix} u' \\ v' \\ 1 \\ \end{bmatrix} = s\cdot P \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \frac{1}{p_{31}u+p_{32}v+p_{33}} \begin{bmatrix} p_{11} &p_{12} &p_{13} \\ p_{21} &p_{22} &p_{23} \\ p_{31} &p_{32} &p_{33} \\ \end{bmatrix} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} \tag{2}\]
用于前视图到俯视图的 IPM 逆透视变换本质上还是透视变换，变换矩阵 \(P\in \mathbb{R}^{3\times3}\) 有 8 个自由度。
2.1. IPM(Inverse Perspective Mapping)
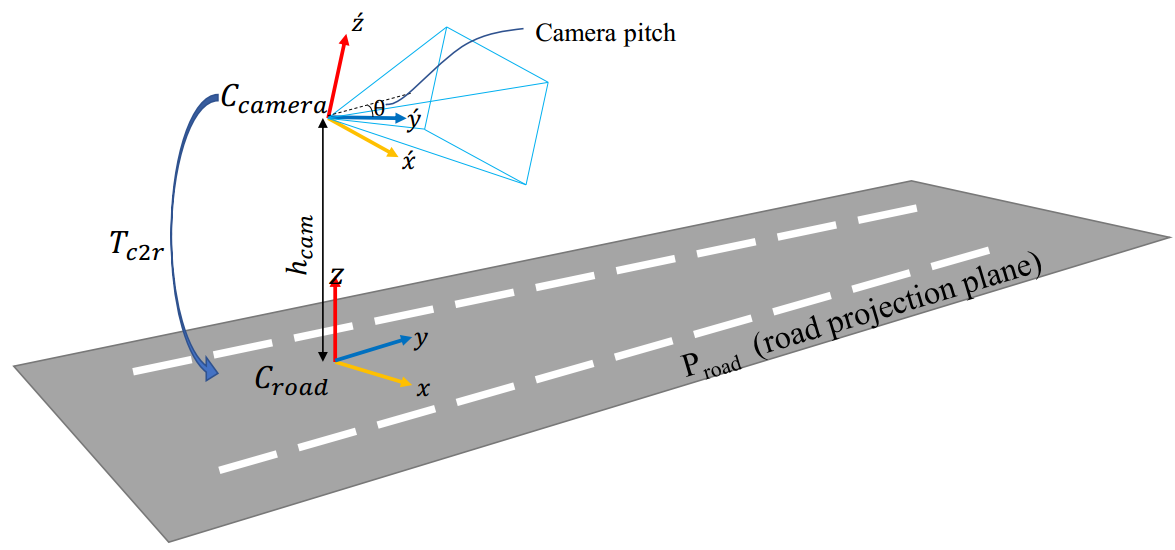世界(road)坐标系与相机坐标系如图 1. 所示，设 \((u',v')\) 表示图像像素坐标系下的点，\((X_w,Y_w,0)\) 表示世界坐标系下地面上的点坐标，\((u,v)\)表示俯视图像素坐标点，IPM 假设地面是平坦的。那么根据相机透视变换原理，可得： \[\begin{align}
\begin{bmatrix}
u' \\
v' \\
1
\end{bmatrix} &= K_{cam}\frac{1}{Z_{cam}}T_{world}^{cam}
\begin{bmatrix}
X \\
Y \\
Z \\
1
\end{bmatrix}_{world}\\ &=
\begin{bmatrix}
f_x &0 &u_0 \\
0 &f_y &v_0\\
0 &0 &1
\end{bmatrix}
\frac{1}{r_{31}X+r_{32}Y+t_z}
\begin{bmatrix}
R &t\\
0 &1
\end{bmatrix}
\begin{bmatrix}
X \\
Y \\
0 \\
1
\end{bmatrix}_{world}\\
&= \frac{1}{r_{31}X+r_{32}Y+t_z}
\begin{bmatrix}
m_{11} &m_{12} &m_{13}\\
m_{21} &m_{22} &m_{23}\\
r_{31} &r_{32} &t_{z}\\
\end{bmatrix}
\begin{bmatrix}
X \\
Y \\
1
\end{bmatrix}_{world} = \frac{Res}{Z_{cam}} P
\begin{bmatrix}
u \\
v \\
1
\end{bmatrix} \tag{3}
\end{align}\]
式 (3) 与式 (2) 形式一致，其中 \(P\) 为相机内参及外参，\(Res\) 为俯视图像素对物理空间尺寸的分辨率，单位为\((meter/pixel)\)。IPM 需要预先标定相机的内外参，尤其是外参 \(R\)，表示与地面平行的世界坐标系与相机成像平面的相机坐标系之间的旋转关系，一般情况下不考虑相机的横滚角以及偏航角，只考虑俯仰角。
2.2. 俯视图求解过程
已知前视图，相机内外参，求解俯视图有两种思路。一种是在世界坐标系下划定感兴趣区域，另一种是在前视图图像上划定感兴趣区域。
2.2.1 世界坐标系下划定感兴趣区域
这种方式很直接，假设世界坐标系下感兴趣区域是 \(x\in [X_{min},X_{max}],y\in [Y_{min},Y_{max}], z\in [Z_{min},Z_{max}]\)，设定 \(Res\)，即可生成俯视图要生成的像素图，然后通过公式 (2) 投影到前视图的亚像素上，用双线性插值获得采样值填入俯视图中即可。
2.2.2 前视图图像上划定感兴趣区域
基于(3)，可以求出世界坐标系下两条平行 \(z\) 轴的平行直线在图像坐标系下的交点，即消失点(Vanishing Point)。假设世界坐标系下平行 \(z\) 轴的直线表示为，点 \((x_a,x_b,x_c)\) 及方向向量 \(k(0,0,1)\)，那么可得该直线上任意一点投影到图像坐标系下表示，当 \(k\) 趋向于无穷大时，即可得到消失点坐标： \[\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \frac{1}{Z_{cam}} M \begin{bmatrix} x_a \\ x_b \\ x_c + k \end{bmatrix}_{world} = \begin{bmatrix} \frac{m_{11}x_a+m_{12}x_b+m_{13}(x_c+k)}{m_{31}x_a+m_{32}x_b+m_{33}(x_c+k)} \\ \frac{m_{21}x_a+m_{22}x_b+m_{23}(x_c+k)}{m_{31}x_a+m_{32}x_b+m_{33}(x_c+k)} \\ 1 \end{bmatrix} \overset{k\to\infty}{\simeq} \begin{bmatrix} \frac{m_{13}}{m_{33}} \\ \frac{m_{23}}{m_{33}} \\ 1 \end{bmatrix} \tag{3} \] 有了图像坐标系下的消失点坐标以后，我们就可以选定需要作透视变换的 ROI 梯形区域(逆透视变换到俯视图后，梯形变矩形)。选定梯形四个角点后，根据像素距离关系，定义俯视图下其对应的矩形框四个像素坐标点，这样能得到四组(2)方程组，足可求解自由度 8 的透视矩阵 \(P\)。OpenCV 有较成熟的函数，更详细的代码原理可见[1]。
3. 其它思考
如果在俯视图下作车道线检测，IPM 是必不可少的。以上 IPM 的缺陷是有一个较强的假设：路面是平坦的。并且时间一长标定参数，尤其是外参会失效，而且距离越远，路面的不平坦导致的逆透视变换误差也会增大。但对于 ADAS 系统来说，车道偏离预警(LDW，Lane Departure Warnings) 中车道线的检测距离在 50m 已经能满足要求。如果要消除更远距离下路面不平坦所带来的影响，也是有方法可以消除的，留到日后再讨论。
按照之前的项目经验，LDW 系统完成度可以很高，基本思路就是 IPM，parsing(segmentation)，clustering，hough，optimization 等几个步骤(这里就不能说得太细了)，更多的精力可能在指标设计及 cornercase 优化上。唯一对用户不太友好的地方就是安装时要进行相机外参(尤其是 pitch 角)的标定，当然标定方法比较简单，我们假设相机坐标系与路面平行，所以透视变换矩阵是固定的，用户只要看路面经过逆透射后，两条 \(z\) 方向的直线是否平行即可。相对于 Mobileye 这种标定巨麻烦的产品，这种标定方式算是非常友好了。此外还可以用自动外参标定方法，脑洞也可以开出很多，效果嘛看具体环境了，需要作谨慎的收敛判断。
