点云目标检测方法已趋于完善，为了能在嵌入式系统上高效运行点云目标检测算法，地平线提出了 AFDet [1]，该文章发表在 CVPR2020 Workshop 上，算是很工程化的一个工作了，对工程产品落地有很好的参考价值。AFDet 应用了很多 Anchor-Free 2D 目标检测思想，可参考 Anchor-Free Detection。
1. Framework
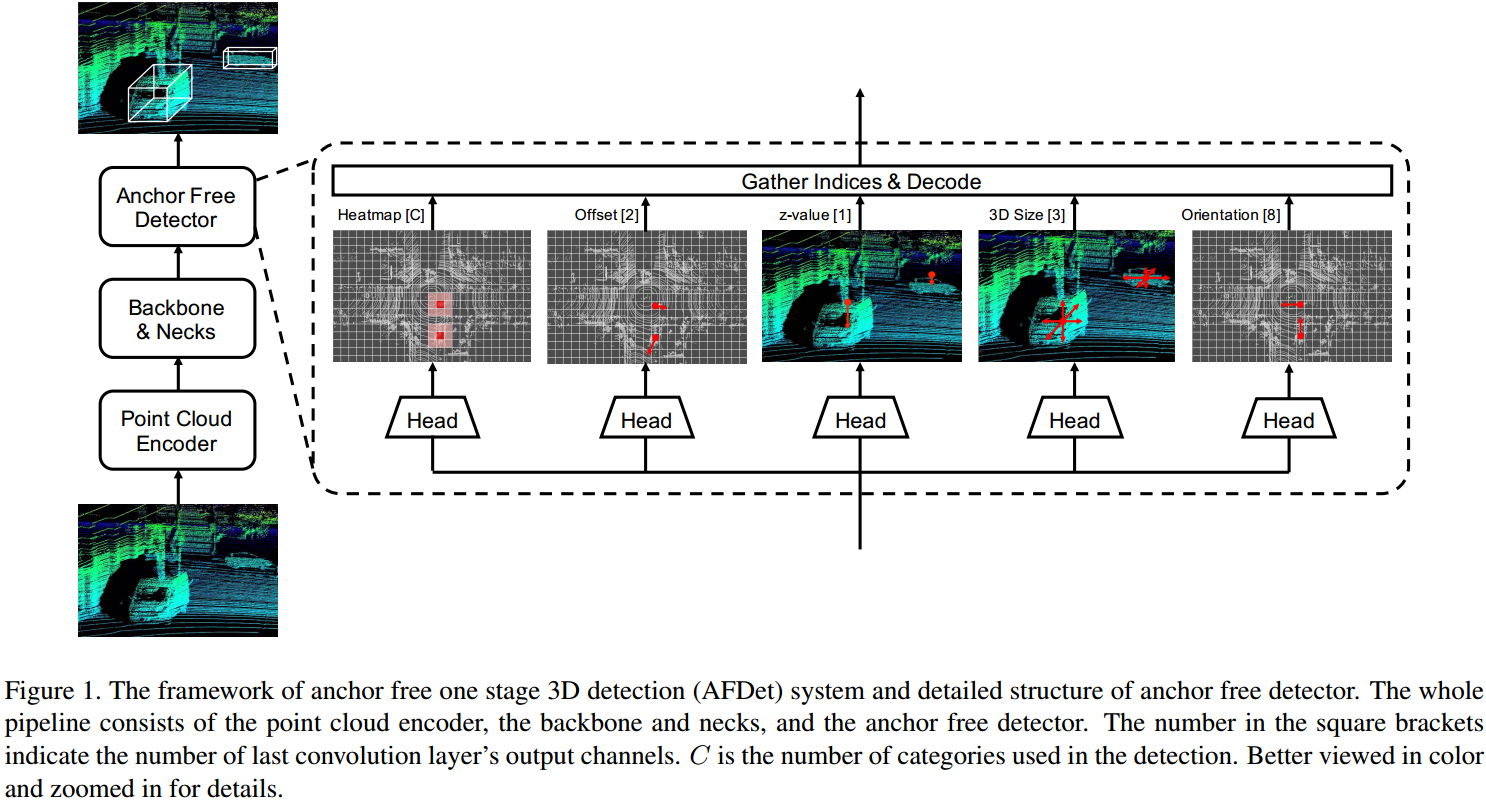AFDet 是一种 Anchor-Free，NMS-Free 的检测方法，所以后处理非常简单，高效。如图 1. 所示，AFDet 采用了传统的 Birdview 下的 Point Cloud Encoder，Backbone & Necks，Anchor-Free Detector 三种网络结构。Point Cloud Encoder 可采用 PointPillars 结构，Backbone & Necks 这里也不作展开。这里最重要的设计是 Anchor-Free 的检测头，由 Keypoint Heatmap，Local Offset Head，z-axis Location Head，3D Object Size Head，Orientation Head 等五个分支构成。
1.1. Keypoint Heatmap & Local Offset Head
BEV 下目标定位由 Heatmap \(M\in\mathbb{R} ^ {W\times H\times C}\) 和 Offset Regression Map \(O\in\mathbb{R} ^ {W\times H\times 2}\) 组成，其中 \(C\) 为 Keypoint 类型。Offset Head 是为了消除 Voxel 后的量化误差以预测更准确的目标位置。
对于第 \(k\) 个类别为 \(c _ k\) 的目标，其 3D 属性为：\((x ^ {(k)},y ^ {(k)},z ^ {(k)},w ^ {(k)},l ^ {(k)},h ^ {(k)},\theta ^ {(k)})\)。设 Pillar 边长为 \(b\)，那么在 BEV 栅格图上，目标中心点作为关键点的坐标为 \(\bar{p}=\left(\left\lfloor\frac{x ^ {(k)}-back}{b}\right\rfloor,\left\lfloor\frac{y ^ {(k)}-left}{b}\right\rfloor\right)\in\mathbb{R} ^ 2\)，其中 \([(back,front),(left,right)]\) 为 \(x-y\) 平面检测范围。由此，目标在 BEV 下的 2D 属性框表示为 \(\left(\left\lfloor\frac{x ^ {(k)}-back}{b}\right\rfloor,\left\lfloor\frac{y ^ {(k)}-left}{b}\right\rfloor,\left\lfloor\frac{w ^ {(k)}}{b}\right\rfloor,\left\lfloor\frac{l ^ {(k)}}{b}\right\rfloor,\theta ^ {(k)}\right)\)。
对于 BEV Heatmap 分支的真值，需要根据目标框真值来生成。对于 Heatmap 中的像素点 \((x,y)\)，设计其值为： \[M _ {x,y,z} =
\left\{\begin{array}{l}
1, &\mathrm{if}\;d=0\\
0.8, &\mathrm{if}\; d=1\\
\frac{1}{d}, &\mathrm{else}
\end{array}\tag{1}\right.\] 其中 \(d\) 表示目标框中心点与对应像素点的距离，Heatmap 中预测量 \(\hat{M} _ {x,y,c}=1\) 表示其为目标框中心点，\(\hat{M} _ {x,y,c}=0\) 则表示是背景。Heatmap 中 \(\bar{p}\) 位置定义为正样本点，其余 Pillars 为负样本点，使用 Focal Loss： \[\mathcal{L} _ {heat} = -\frac{1}{N}\sum _ {x,y,c}
\left\{\begin{array}{l}
\left(1-\hat{M} _ {x,y,c}\right) ^ {\alpha}\;\mathrm{log}\left(\hat{M} _ {x,y,c}\right), \;\mathrm{if}\; M _ {x,y,c} = 1 \\
\left(1-M _ {x,y,c}\right) ^ {\beta}\; \left(\hat{M} _ {x,y,c}\right) ^ {\alpha}\mathrm{log}\left(1-\hat{M} _ {x,y,c}\right), \;\mathrm{else} \\
\end{array}\tag{2}\right.\] 另一方面，Offset Regression 分支可以解决量化误差，以及当 Heatmap 中心点分类错误的时候，补救预测准确的中心点位置。选择中心点周围半径 \(r\) 区域作 Offset 预测： \[\mathcal{L} _ {off} = \frac{1}{N}\sum _ p\sum ^ r _ {\sigma =-r}\sum ^ r _ {\epsilon = -r}\left\vert\hat{O} _ {\bar{p}}-b(p-\bar{p}+(\sigma,\epsilon))\right\vert\tag{3}\] 只对 \(2r+1\) 的矩形区域作 Offset 预测。
1.2. z-axis Location Head
高度预测值 \(\hat{Z}\in\mathbb{R} ^ {W\times H\times 1}\)，其 Loss 为： \[\mathcal{L _ z} = \frac{1}{N}\sum _ {k=1} ^ N\left\vert\hat{Z} _ {p ^ {(k)}}-z ^ {(k)}\right\vert\tag{4}\]
1.3. 3D Object Size Head
尺寸预测值 \(\hat{S}\in\mathbb{R} ^ {W\times H\times 3}\)，其 Loss 为： \[\mathcal{L} _ {size} = \frac{1}{N}\sum _ {k=1} ^ N\left\vert\hat{S} _ {p ^ {(k)}}-s ^ {(k)}\right\vert\tag{5}\] 其中 \(s ^ {(k)} = (w ^ {(k)},l ^ {(k)}, h ^ {(k)})\)。
1.4. Orientation Head
与传统的一样，将角度预测分解为 bin 分类＋ offset 回归两个任务。具体的，分成两个 bin：\(\Psi _ 1 =[-\frac{7\pi}{6}, \frac{\pi}{6}]\)；\(\Psi _ 2 =[-\frac{\pi}{6}, \frac{7\pi}{6}]\)。对于每个 bin，softmax 分类 \(\hat{\mu} _ i ^ {(k)}\in\mathbb{R} ^ 2\)，与 bin 中心夹角 \(\gamma _ i\) 的 sin/cos 值 \(\hat{v} _ i ^ {(k)}\)。Loss 为： \[\mathcal{L} _ {ori} = \frac{1}{N}\sum _ {k=1}^N\sum _ {i=1}^2\left(\mathrm{softmax}\left(\hat{\mu} _ i ^ {(k)},\eta _ i ^ {(k)}\right)+\eta _ i ^ {(k)}\left\vert\hat{v} _ i ^ {(k)}-v _ i ^ {(k)}\right\vert\right)\tag{6}\] 其中当 \(\theta ^ {(k)}\in\Psi _ i\) 时，\(\eta _ i ^ {(k)} = \mathbb{1}\)，\(v _ i^ {(k)}=\left(\mathrm{sin}(\theta ^ {(k)}-\gamma _ i), \mathrm{cos}(\theta ^ {(k)}-\gamma _ i)\right)\)。由此，预测的角度可通过如下方式解码： \[\hat{\theta} ^ {(k)}=\mathrm{arctan2}\left(\hat{v} _ {j,1} ^ {(k)},\hat{v} _ {j,2} ^ {(k)}\right)+\gamma _ j\tag{7}\] 因为是 Anchor Free 的方式，所以如果按照传统的方式， bin 数量较大，那么最后输出的 map 所占的内存也会相当大，所以这里只采用了两个 bin。这么做有很大好处，比如量化时数值的稳定性，所以在工程应用中非常值得借鉴思考。
2. Experiments
如图 2. 所示，AFDet 在同等计算量下，基本能达到 PointPillars 水平。图 3. 则对比了几种 Anchor-Based 方法，效果也较好。
3. Reference
[1] Ge, Runzhou, et al. "Afdet: Anchor free one stage 3d object detection." arXiv preprint arXiv:2006.12671 (2020).
