目前点云特征学习在学术界还处于各种探索阶段，PointCloud-Feature-Extraction 中将点云特征提取分为三维物理空间操作以及映射空间操作两大类，其中对直接在三维空间中提取特征的操作进行了较详细的分析。由于变换到映射空间的操作会相对比较复杂，目前为了实时应用，本人还是比较倾向于直接在三维空间进行操作。
类比图像特征提取，直接在三维空间进行点云特征提取的基本操作有：
- 局部点云特征提取：对目标点的周围点特征进行融合，从而得到该目标点特征；
- 上采样/下采样：采样以扩大感受野，进一步提取局部/全局信息；
PointCloud-Feature-Extraction 主要描述了已知周围点位置后，局部点云特征的提取方式，考虑的是特征提取的有效性，重写该问题为：针对待提取特征的坐标点 \(\mathcal{x} _ c\)，融合其周围 \(K\) 个点的操作： \[ \tilde{f_c} = \mathcal{A}\left(\{e(\mathcal{x_i,x_c},f_c, f_i)\ast \mathcal{M}(f_i)\}, i\in1,...,K \right) \tag{1}\] 其中 \(f_i\) 为点 \(\mathcal{x_i}\) 的特征，\(\mathcal{M}\) 为多层感知机；\(e,\mathcal{A}\) 分别为周围点特征权重函数以及特征聚合函数，大致对应 PointCloud-Feature-Extraction 中的 \(h_\theta\) 以及 \(\Box\)。本文则思考这两个基本操作如何计算加速以能实时应用。具体来看，耗时操作主要是：
- Sampling
- Points Querying
[1] 提出了一种基于 Voxel 的快速采样方法，并依赖 Voxel 做近似而快速的 Points Querying，以下作详细分析。
1. Overview
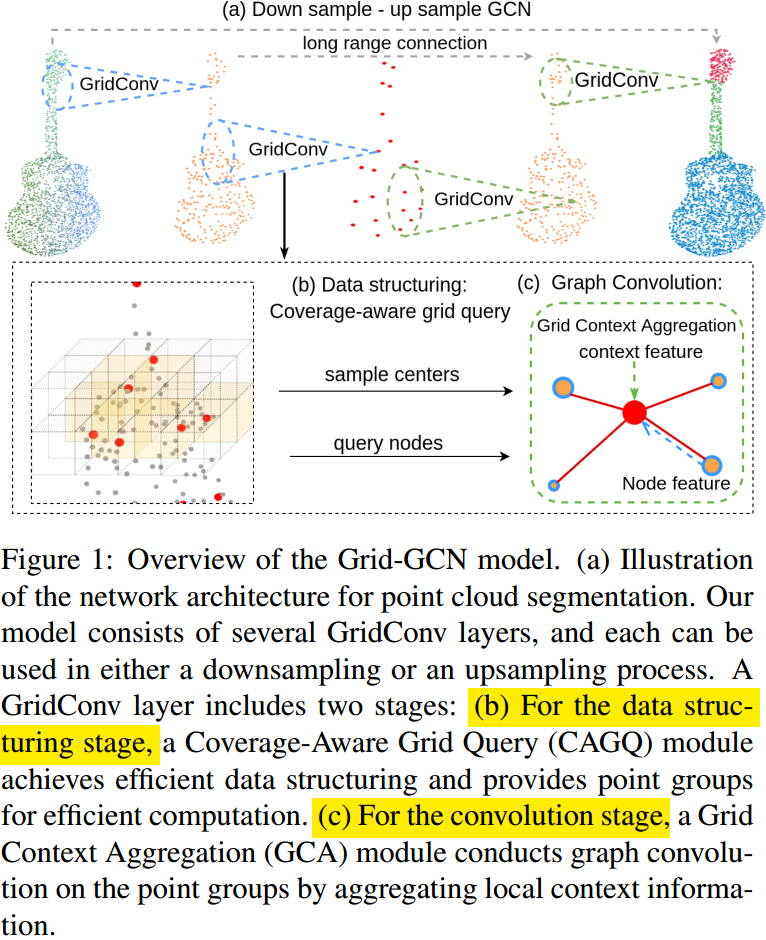如图 1. 所示，Grid-GCN 模型目标是提取点级别的特征，从而可以作 semantic segmentation 等任务。基本模块为 GridConv，该模块又包括数据的构建-Coverage-aware Grid Query(CAGQ)，以及图卷积-Grid Context Aggregation(GCA)。 
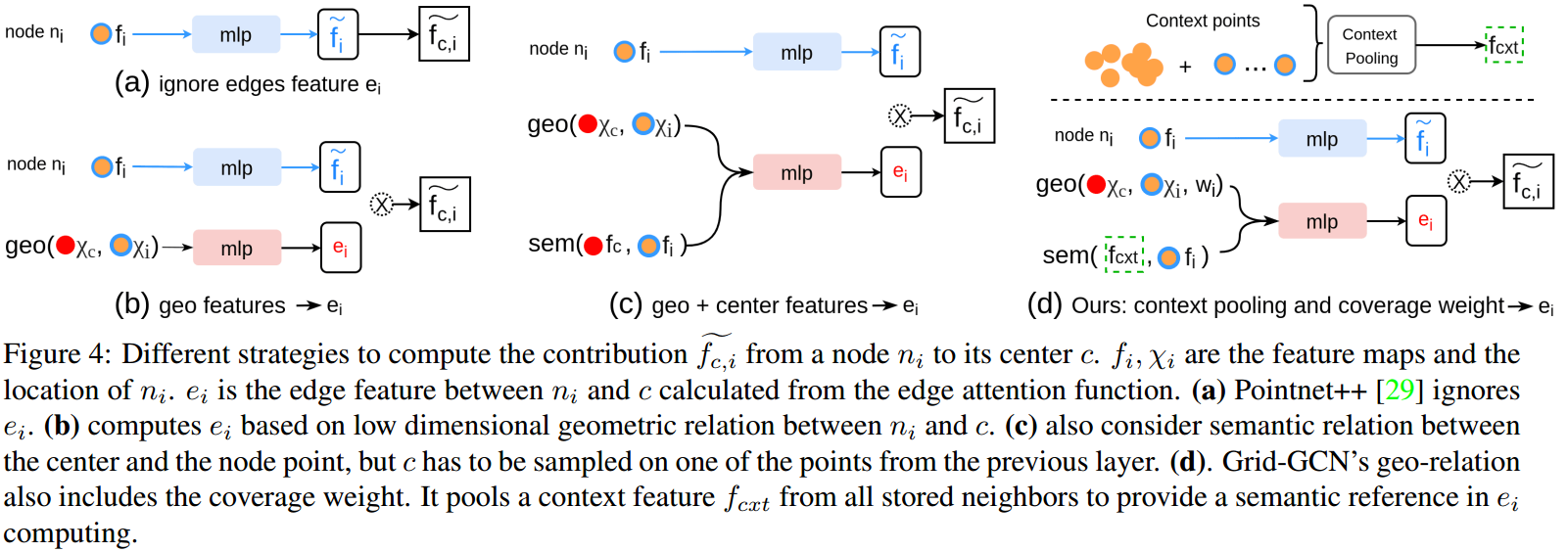GCA 操作如图 2. 所示，与 PointCloud-Feature-Extraction 中介绍的方法都大同小异，当信息量累加到一定程度后，基本只有一两个点的 mAP 差异，这里不作展开。
CAGQ 则包含 sampling 与 points querying 两个核心且又最耗时的操作，CAGQ 能极大提升这两个操作的速度。首先定义三维 voxel 大小 \((v_x,v_y,v_z)\)，那么对于点 \(x,y,z\)，其 voxel 索引为 \(Vid(u,v,w)=floor\left(\frac{x}{v_x},\frac{y}{v_y},\frac{z}{v_z}\right)\)，每个 voxel 限制点数量为 \(n_v\)。假设 \(O_v\) 为非空的 voxel 集合，采样 \(M\) 个 voxel \(O_c\subseteq O_v\)。对于每个 voxel \(v_i\)，定义其周围的 voxel 集合为 \(\pi(v_i)\)，该集合中的点则构成 context points。由此可知要解决的问题：
- Sampling：采样 voxel 集合 \(O_c\subseteq O_v\)；
- Points Querying：从 Context Points 中选取 K 个点；
2. Sampling
FlowNet3D 中大致阐述过几种采样方法，信息保留度较高的方法是 FPS，但是速度较慢。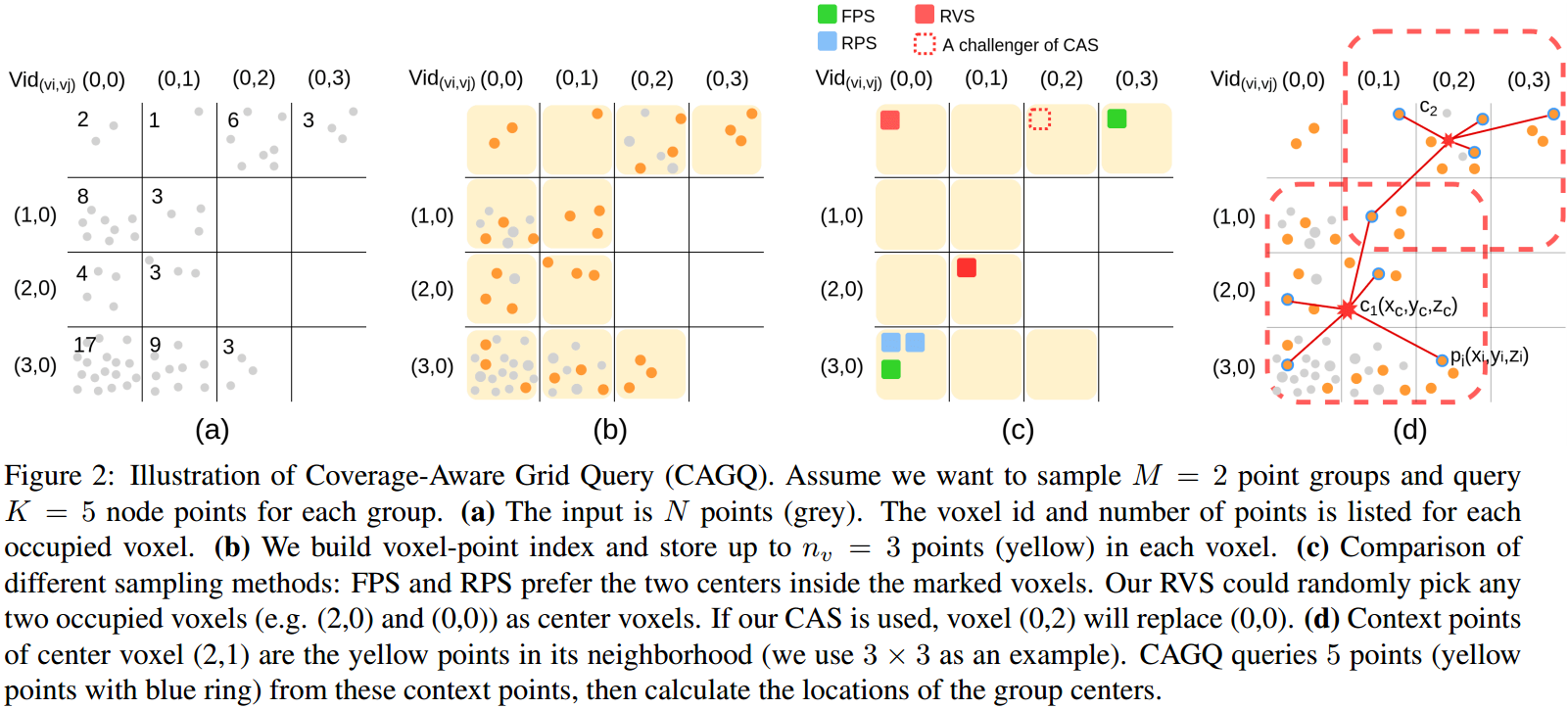 
如图 3. 所示，本文提出了两种基于 voxel 的采样方法:
- Random Voxel Sampling(RVS)
对每个 voxel 进行随机采样，相比对每个点进行随机采样(Random Point Sampling)，RVS 有更少的信息损失，更广的空间信息覆盖率。 - Coverage-Aware Sampling(CAS)
在 RVS 基础上，CAS 有更广的信息覆盖率，其步骤为：- 随机采样 \(M\) 个 voxel，即执行 RVS；
- 对未被采样到的 voxel \(v_c\)，计算如果加入这个 voxel，空间覆盖率增益： \[ H_{add} = \sum_{v\in \pi(v_c)}\delta(C_v) - \beta\frac{C_v}{\lambda} \tag{2}\] 对采样集里面的 voxel \(v_i\)，计算如果去掉这个 voxel，空间覆盖率减少量： \[ H_{rmv} = \sum_{v\in \pi(v_i)}\delta(C_v-1) \tag{3}\]
- 如果 \(H_{add} > H_{rmv}\)，则进行替换；
- 迭代 2,3 步骤；
其中 \(\delta(x)=1,if x=0,else\,0\)。\(\lambda\) 为周围 voxel 个数，\(C_v\) 是采样集覆盖该 voxel 的个数。
3. Points Querying
传统的 Points Querying 一般是在所有点中建立 KD-Tree 或 Ball Query 形式来找某点的邻近点。本文在 voxel 基础上来快速寻找邻近点，提供了两种方法：
- Cube Query
这是一种近似法，直接在 Context Points 中随机采样 \(K\) 个点作为最近邻点。从物理意义上将，最近邻的区域的点特征应该都是相似的，所以这种近似法应该会很有效。 - K-Nearest Neighbors
在 Context Points 中寻找 K-NN，相比在全点云中找 K-NN，这种方法搜索速度会非常快。
4. Experiments
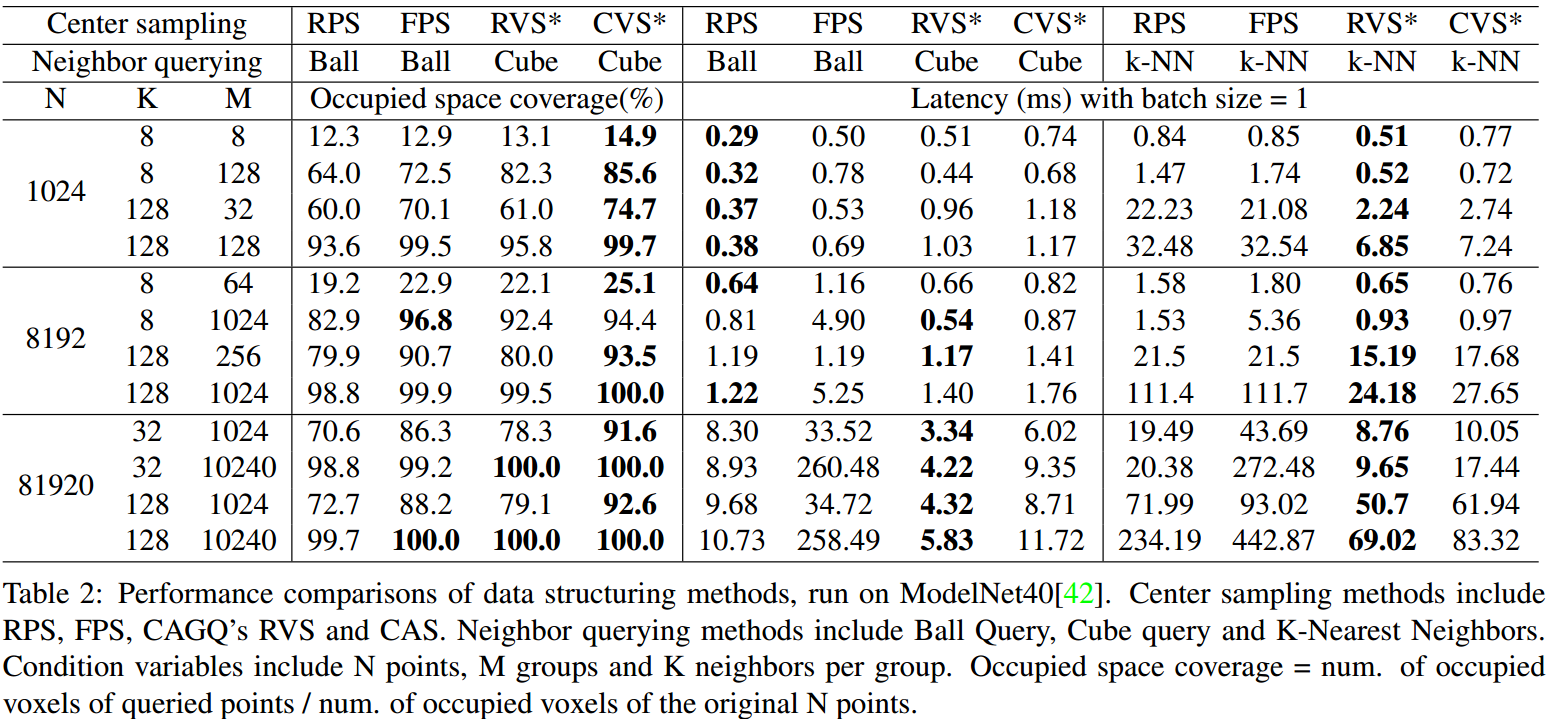如图 4. 与图 5. 所示，比较了 RPS，FPS，RVS，CAS 等采样算法的时间复杂度与空间覆盖率，以及 Ball Query，Cube Query，K-NN 等 Points Query 算法的时间复杂度。由此可见，本文提出的 Sample 及 Points Query 算法非常高效。
5. reference
[1] Xu, Qiangeng. "Grid-GCN for Fast and Scalable Point Cloud Learning." arXiv preprint arXiv:1912.02984 (2019).
