基于点云的 Instance Segmentation 方法之前已经介绍过几种，其中将点云在 Bird-View 进行 Instance Segmentation 的思路基本与图像 Instance Segmentation 相似。本文[1] 介绍一种图像 Instance Segmentation 方法，其能处理各种尺寸的目标，以及不用做聚类后处理，可直接得到目标实例。由于能处理较大尺寸的目标，所以也能应用于车道线检测领域，其思路值得借鉴。
1. Framework
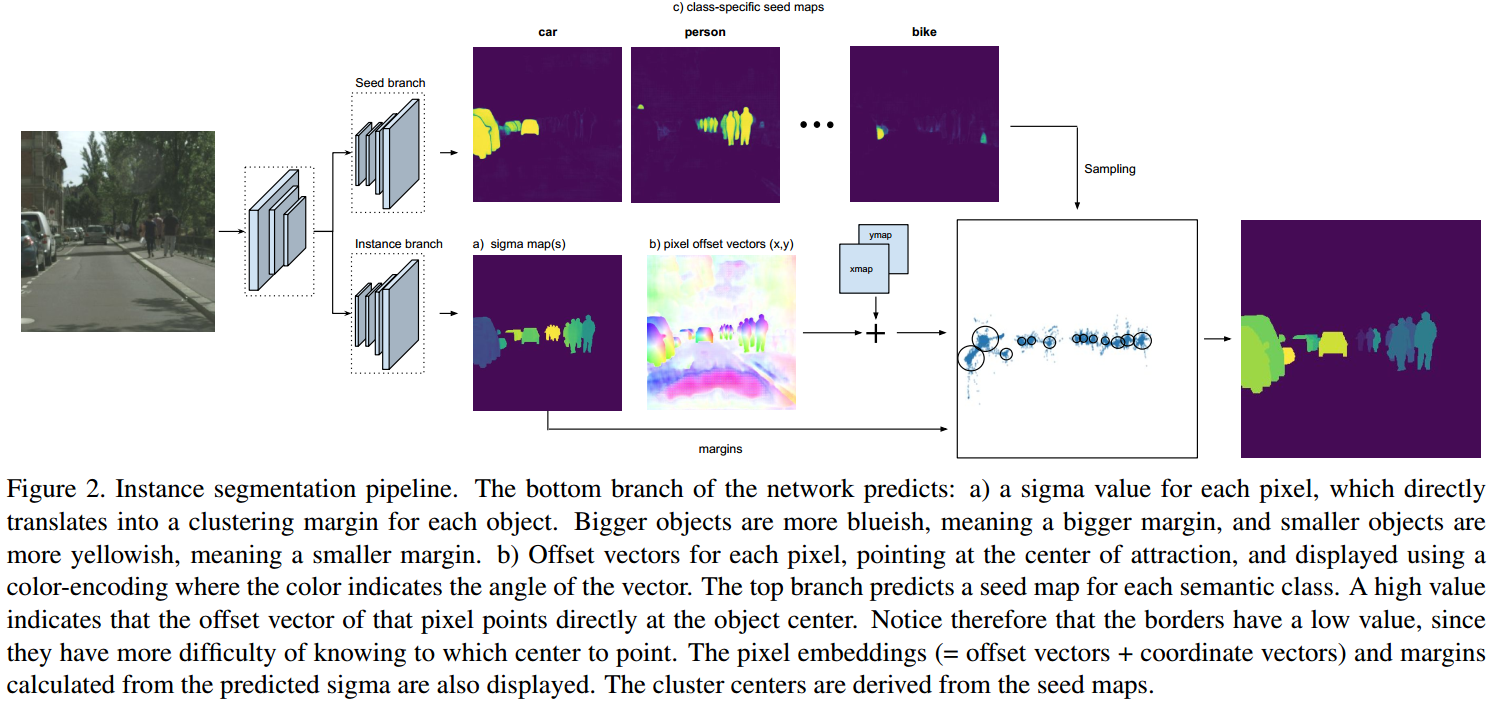如图 1. 所示，网络输出 Seed Branch 以及 Instance Branch。Seed Branch 中分数较高的表示每个类别每个实例的中心点，中心点具体坐标由该像素坐标以及对应的 offset 预测值决定。
Instance Branch 输出 offset vectors 以及 sigma maps。offset vectors 表示该像素点指向的对应实例的中心位置；sigma maps 表示 offset 指向中心的宽松度，是本方法能预测较大尺寸目标的关键。
2. Loss
Instance Segmentation 的目标是将一堆二维像素点 \(\mathcal{X}=\{x _ 0, x _ 1, ..., x _ N\}\)，聚类成实例 \(\mathcal{S} = \{S _ 0, S _ 1, ..., S _ K\}\)。
2.1. Instance Branch
传统的做法是将每个像素点 \(x _ i\) 回归其与对应实例中心 \(C _ k=\frac{1}{N}\sum _ {x\in S _ k} x\) 的 offset 向量 \(o _ i\)，得到的 \(e _ i=x _ i+o _ i\) 即为该像素点指向的实例中心点。Loss 设计为： \[\mathcal{L} _ {regr} = \sum _ {i=1} ^ n\Vert o _ i-\hat{o} _ i\Vert\tag{1}\] 其中 \(\hat{o} _ i=C _ k-x _ i\)。
因为 \(e _ i\) 很难正好指向实例中心点，所以引入 hinge loss，让其指向实例中心周围 \(\sigma\) 范围区域： \[\mathcal{L} _ {hinge} = \sum _ {k=1} ^ K\sum _ {e _ i\in S _ k}\mathrm{max}(\Vert e _ i-C _ k\Vert-\sigma, 0) \tag{2}\] 从而保证： \[e _ i\in S _ k \iff \Vert e _ i-C _ k\Vert < \sigma \tag{3}\] 但是这种方法需要根据最小目标来选择 \(\sigma\) 值，对于大目标，选取的 \(\sigma\) 又不太合理。
为了选取的 \(\sigma\) 能处理不同尺寸的实例目标，本文设计网络输出 sigma maps，在以实例中心为高斯概率分布下，每个像素属于该实例的概率为： \[\phi _ k(e _ i) = \mathrm{exp}\left(-\frac{\Vert e _ i-C _ k\Vert ^ 2}{2\sigma _ k ^ 2}\right)\tag{4}\] 当 \(\phi _ k(e _ i) > 0.5\) 时，表示该像素点属于该实例。即： \[e _ i\in S _ k \iff \mathrm{exp}\left(-\frac{\Vert e _ i-\hat{C} _ k\Vert ^ 2}{2\hat{\sigma} _ k ^ 2}\right) > 0.5 \tag{5}\] 由此像素回归指向中心点的区域可由 \(\sigma\) 控制： \[\mathrm{margin} = \sqrt{-2\sigma _ k ^ 2\mathrm{ln}0.5} \tag{6}\] 进一步得，可将 \(\sigma\) 分解为两个方向的值，形成椭圆状的二维高斯分布，这样能适应狭长型的目标： \[\phi _ k(e _ i) = \mathrm{exp}\left(-\frac{\Vert e _ {ix}-C _ {kx}\Vert ^ 2}{2\sigma _ {kx} ^ 2}-\frac{\Vert e _ {iy}-C _ {ky}\Vert ^ 2}{2\sigma _ {ky} ^ 2}\right)\tag{7}\] 以及，可将实例中心点像素坐标向量用特征向量代替： \[\phi _ k(e _ i) = \mathrm{exp}\left(-\frac{\Vert e _ i-\frac{1}{\vert S _ k\vert}\sum _ {e _ j\in S _ k}e _ j\Vert ^ 2}{2\sigma _ k ^ 2}\right)\tag{8}\] \(\sigma _ k\) 定义为： \[\sigma _ k=\frac{1}{\vert S _ k\vert}\sum _ {\sigma _ i\in S _ k}\sigma _ i\tag{9}\] 采用 Lovase-hinge loss 作用于像素点属于对应实例的概率图，\(\sigma\) 通过概率图隐式地学到。以及为了保证式 (9) 的一致性，增加 \(\sigma\) 平滑 Loss： \[\mathcal{L} _ {smooth}=\frac{1}{\vert S _ k\vert}\sum _ {\sigma _ i\in S _ k}\Vert\sigma _ i-\sigma _ k\Vert ^ 2\tag{10}\]
2.2. Seed Branch
实例中心点的预测采用回归方法，背景点标签为零，前景标签是以实例中心为原点的高斯分布。Loss 设计为： \[\mathcal{L} _ {seed} = \frac{1}{N}\sum _ i ^ N\mathbb{1} _ {\{s _ i\in S _ k\}}\Vert s _ i-\phi _ k(e _ i)\Vert ^ 2+\mathbb{1} _ {\{s _ i\in\mathbf{bg}\}}\Vert s _ i-0\Vert ^ 2 \tag{11}\] 此时 \(\phi _ k(e _ i)\) 不作梯度反传。
3. Reference
[1] even, Davy, et al. "Instance segmentation by jointly optimizing spatial embeddings and clustering bandwidth." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019.
