3D 目标检测中，目标定位的不确定性也很关键，Heteroscedastic Aleatoric Uncertainty 中已经较为详细的描述了在 Bayesian Deep Networks 中如何建模异方差偶然不确定性(Aleatoric Uncertainty)。在贝叶斯深度神经网络框架下，网络不仅预测目标的位置(Mean)，还预测出该预测位置的方差(Variance)。本文[1] 延续了 Heteroscedastic Aleatoric Uncertainty 中预测 Corner 点位置方差的思路，提出了一种预测目标位置方差的方法。
1. 算法框架
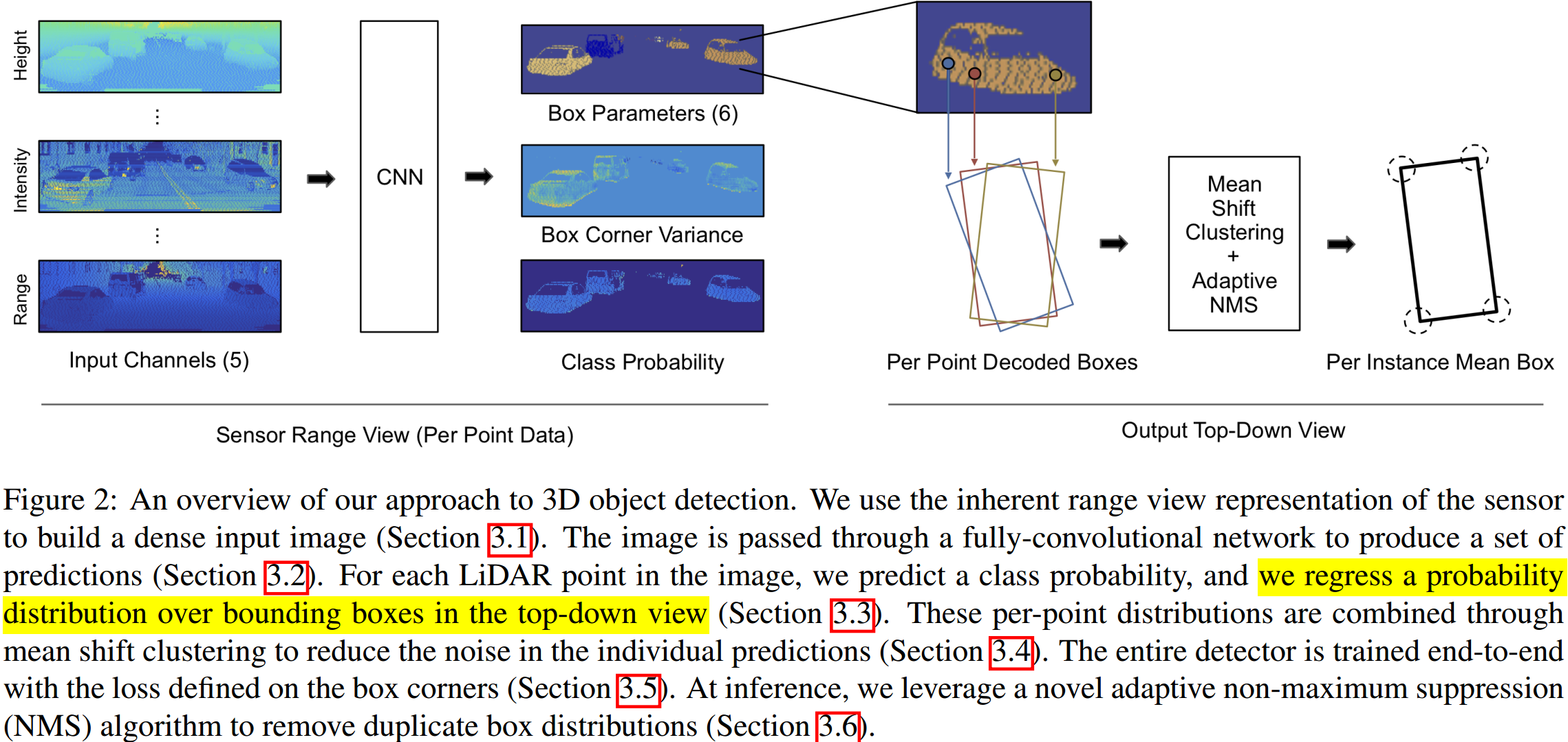如图 1. 所示，输入为激光点云的 Sensor Range View 表示方式，输出为点级别的目标框3D属性，框顶点位置方差，以及类别概率。最后在 Bird View 下作目标框的聚类与 NMS 等后处理。
1.1. 点云输入方式
不同于目前主流的 Bird View 点云栅格化方式，本文将点云直接根据线束在 Sensor Range View 下进行表示，高为激光线数量，宽为 HFOV 除以角度分辨率。设计 5 个 channel：距离，高度，角度，反射值，以及是否有点的标志位。
本文认为这种点云表示方式的优点被忽视了，该视角下，点云的表达是紧促的，而且能高效得取得局部区域点，此外，能保留点云获取方式的信息。另一方面，该表达方式的缺点有，访问局部区域时，并不是空间一致的；以及需要处理物体的不同形状和遮挡问题。本文实验结果是，在 Kitti 上效果不如 Bird View 方法，但是在一个较大数据集上，能克服这些缺点。
1.2. 网络输出
网络输出为点级别的预测，由三部分组成：
- 类别概率
每个类别的概率； - 3D 框属性
包括相对中心距离 \((d _ x, d _ y)\)；相对朝向 \((\omega _ x, \omega _ y)=(\mathrm{cos}\omega, \mathrm{sin}\omega)\)；以及尺寸 \((l,w)\)。最终目标框中心点位置及朝向表示为： \[\left\{\begin{array}{l} \mathbf{b} _ c = [x,y]^T+\mathbf{R} _ \theta [d _ x,d _ y]^T \\ \varphi = \theta + \mathrm{atan2}(\omega _ y,\omega _ x) \end{array}\tag{1}\right.\] 其中 \(\theta\) 为该点的雷达扫描角度。由此可得到四个目标框角点坐标： \[\left\{\begin{array}{l} \mathbf{b} _ 1 = \mathbf{b} _ c + \frac{1}{2}\mathbf{R} _ \varphi [l,w]^T\\ \mathbf{b} _ 2 = \mathbf{b} _ c + \frac{1}{2}\mathbf{R} _ \varphi [l,-w]^T\\ \mathbf{b} _ 3 = \mathbf{b} _ c + \frac{1}{2}\mathbf{R} _ \varphi [-l,-w]^T\\ \mathbf{b} _ 4 = \mathbf{b} _ c + \frac{1}{2}\mathbf{R} _ \varphi [-l,w]^T \end{array}\tag{2}\right.\] - 顶点位置方差
当观测不完全时(遮挡，远处)，目标框的概率分布是多模态的，所以如 Heteroscedastic Aleatoric Uncertainty 中所述，输出为混合高斯模型。对于每个点的每个类别，输出 \(K\) 个目标框属性：\(\{d _ {x,k}, d _ {y,k}, \omega _ {x,k}, \omega _ {y,k}, l _ k, w _ k\} _ {k=1}^K\)；对应的方差 \(\{s _ k\} _ {k=1}^K\)；以及模型权重 \(\{\alpha _ k\} _ {k=1}^K\)。
1.3. Bird View 后处理
网络其实就做了一个点级别的分割，接下来需要作聚类以得到目标框。本文采用 Mean-Shift 方法作聚类。由于是点级别的概率分布，得到目标点集后，需要用 BCN(详见 MOT-Fusion) 转换为目标级别的概率分布： \[\left\{\begin{array}{l} \hat{\mathbf{b}} _ i = \frac{\sum _ {j\in S _ i} w _ j\mathbf{b} _ j}{\sum _ {j\in S _ i}w _ j}\\ \hat{\sigma} _ i^2 = \left(\sum _ {j\in S _ i}\frac{1}{\sigma ^2 _ j}\right)^{-1} \end{array}\tag{3}\right.\] 其中 \(w=\frac{1}{\sigma ^ 2}\)。
2. Loss 形式
分类采用 Focal Loss。对于每个点 3D 属性的回归，首先找到最靠近真值的预测模型： \[k ^ * = \mathrm{arg}\min \limits _ k\Vert\hat{\mathbf{b}} _ k-\mathbf{b} ^{gt}\Vert\tag{4}\] 对该预测模型作 Loss： \[\mathcal{L} _ {box}=\sum _ n\frac{1}{\hat{\sigma} _ {k ^ * }} \left\vert\hat{\mathbf{b}} _ {n,k^ * }-\mathbf{b} _ n^{gt}\right\vert + \mathrm{log}\hat{\sigma} _ {k ^ * }\tag{5}\] 实际回归的是 \(s:=\mathrm{log} \sigma\)。然后对混合模型的权重 \(\{\alpha _ k\} _ {k=1}^K\) 作 cross entry loss \(\mathcal{L} _ {mix}\)。最终的回归 Loss 为： \[\mathcal{L} _ {reg} = \frac{1}{N}\sum _ i \frac{\mathcal{L} _ {box, i} + \lambda \mathcal{L} _ {mix,i}}{n _ i} \tag{6}\]
3. Adaptive NMS
类别概率不能反应目标框的质量，所以本文采用预测的目标框方差作为 NMS 的参考量。将目标框方差转换为目标框的质量分数：\(\alpha _ k/2\hat{\sigma} _ k\)。
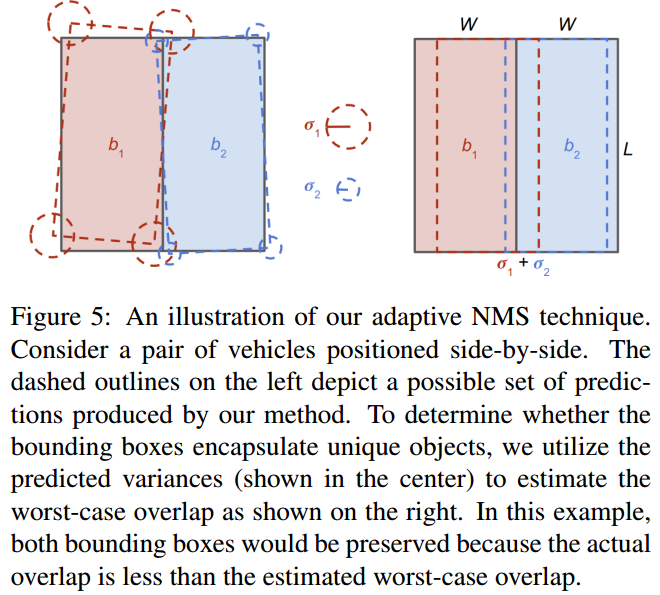此外不同目标在 Bird-View 下 IoU 最大值有一定的限制，如图 2. 所示，最坏的情况，Bird-View 下两个框的 IoU 最大限制为设计为： \[t=\left\{\begin{array}{l}
\frac{\sigma _ 1+\sigma _ 2}{2w-\sigma _ 1 - \sigma _ 2} & \sigma _ 1+\sigma _ 2 < w\\
1 & otherwise
\end{array}\tag{7}\right.\] 当两个目标框的 IoU 大于阈值时，可能的情况是：1. 目标框错误，则删除低分数的目标框；2. 方差估计错误，那么增大方差使最大阈值满足 IoU 条件。
4. 预测分布的分析
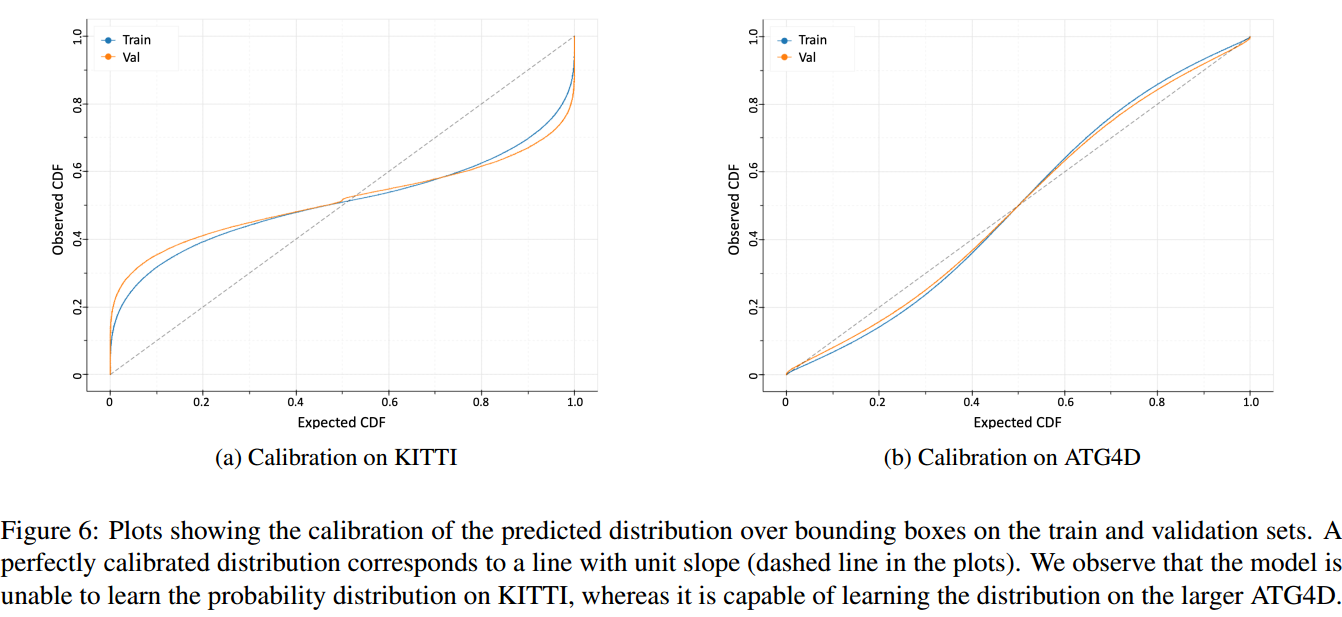评价 Variance(Uncertainty) 预测的好坏，可以画 Calibration 图。如图 3. 所示，横坐标为预测的 Mean 与真值形成的高斯概率分布下的 CDF，而纵坐标为预测的 Variance 统计出的高斯分布下的 CDF。理想情况下，两者是 \(y=x\) 的关系，如图所示，在 ATG4D 大数据集上，预测的 Variance 效果更好。
5. 一些思考
不管是 2D 检测还是 3D 检测，这种先(语义)分割后聚类出目标的思想，有很强的优势：召回率高，超参数少，自带分割信息等。本文又应用 Aleatoric Uncertainty 来建模检测的不确定性--位置方差(不确定性干嘛用，怎么用，不多说了)，有很好的借鉴意义。
6. Reference
[1] Meyer, Gregory P., et al. "Lasernet: An efficient probabilistic 3d object detector for autonomous driving." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019.
