剪枝是神经网络加速的重要手段之一，Pruning 中较详细的描述了剪枝的特性与基本方法，Filter-Pruning 则描述了卷积核剪枝的基本方法。Filter Pruning 属于结构化剪枝(Structure Pruners)，能在不改变硬件计算单元的情况下，提升网络计算速度。本文[1] 就属于 Filter Pruning 方法，简单有效，较为经典。
1. Framework
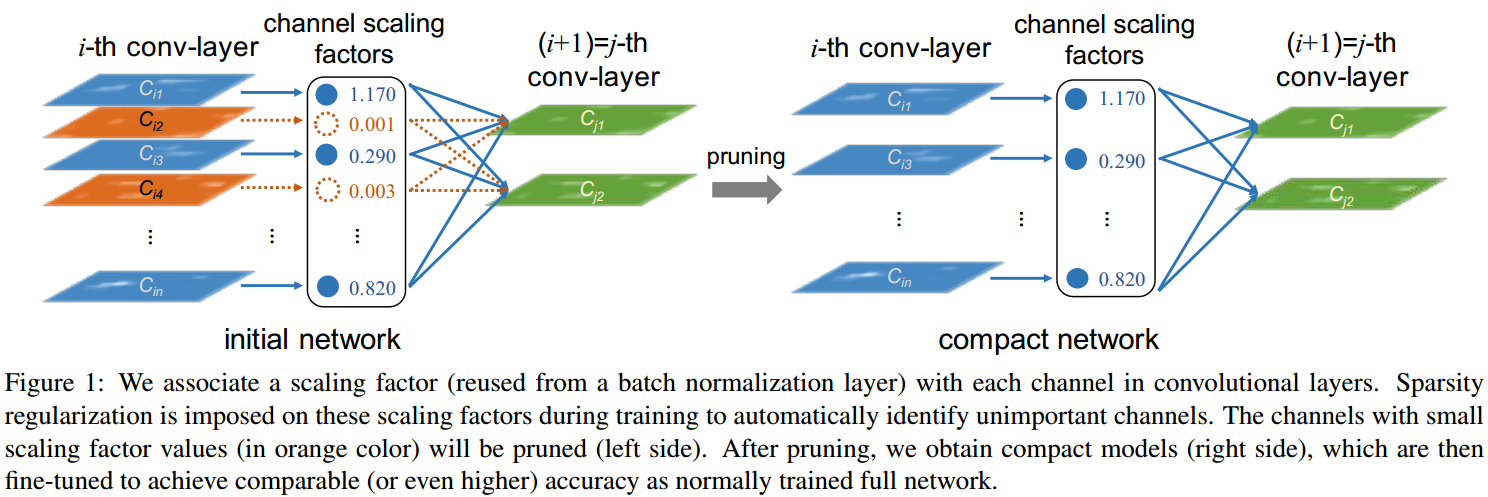如图 1. 所示，本文提出的方法非常简单：将各通道特征(对应各卷积核)乘以一个尺度系数，并用正则化方法来稀疏化尺度系数。训练后卷积核对应的较小的尺度，则认为其不重要，进行剪枝。最终 Fine-Tune 剩下的网络即可。
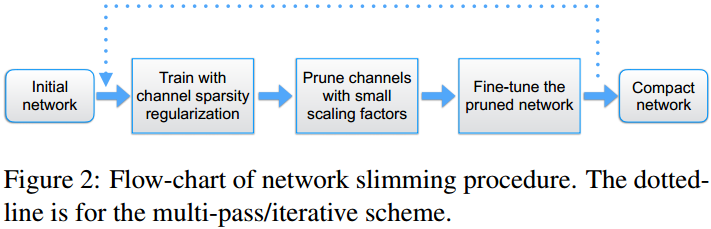其剪枝及 Fine-Tune 过程如图 2. 所示，可迭代进行，以获得最优的剪枝效果。
实际操作中用 BN 层中的 \(\gamma\) 系数来代替该尺度系数。BN 层计算过程为： \[\hat{z}=\frac{z _ {in}-\mu _ {\mathcal{B}}}{\sqrt{\sigma _ {\mathcal{B}} ^ 2 + \epsilon}}; \; z _ {out}=\gamma \hat{z}+\beta\tag{1}\] 其中 \(z _ {in}, z _ {out}\) 表示 BN 层的输入输出，\(\mathcal{B}\) 表示当前 mini-batch，\(\mu _ {\mathcal{B}},\sigma _ {\mathcal{B}}\) 表示 mini-batch 中 channel-wise 的均值和方差，\(\gamma,\beta\) 为可训练的 channel-wise 的尺度及偏移系数。
对 \(\gamma\) 进行 L1 正则化，较小的 \(\gamma\) 对应的卷积核即认为是不重要的，可裁剪掉。
2. Thinking
本方法非常简单，但是为什么仅凭较小的 \(\gamma\) 即可确定对应的卷积核不重要呢？我的思考如下：
- 为什么不需要考虑卷积核的 L1 值？
因为 BN 的 \(\mu _ {\mathcal{B}},\sigma _ {\mathcal{B}}\) 将输出归一化了，所以卷积核的值幅度对之后没有影响，故其值幅度无法体现其重要性； - 为什么不需要考虑 \(\beta\) 值？
因为 \(\beta\) 只会影响输出特征的均值，而不会影响输出特征的方差，神经网络的表达能力在于特征的方差，而不是均值，故 \(\gamma\) 才能体现卷积核的重要性，而 \(\beta\) 不能。
3. Reference
[1] Liu, Zhuang, et al. "Learning efficient convolutional networks through network slimming." Proceedings of the IEEE International Conference on Computer Vision. 2017.
