基于点云的 3D 感知一般通过 3D 目标框实现，但是如果直接网络出 3D 目标框属性，那么召回率很难达到非常高的水平(所以之前提到检测的任务可以分解为分割+后处理聚类来作，这样召回率会比较高)。本文提出的 MotionNet[1] 用于检测俯视图下每个栅格的类别及轨迹，可作为检测的辅助，能召回更小的目标，以及没有标注的动态障碍物目标。这种栅格级别或点级别的目标探测能力相比直接出目标框的优势有：
- 目标框形式一般依赖于目标框区域的特征，不同目标类别之间的特征很难泛化，所以无法检测未见过的类别；
- 目标框形式一般会作 NMS 等处理去掉不确定性较大的框，而栅格级别的会保留；
如图 1. 所示，对于轮椅这种非正常类别(或预定义类别)的目标，检测任务可能会失效，此时 MotionNet 则会根据时序信息输出该区域的目标速度(未来运动轨迹)，这可作为 Motion Planning 阶段的另一重要线索。
1. Framework
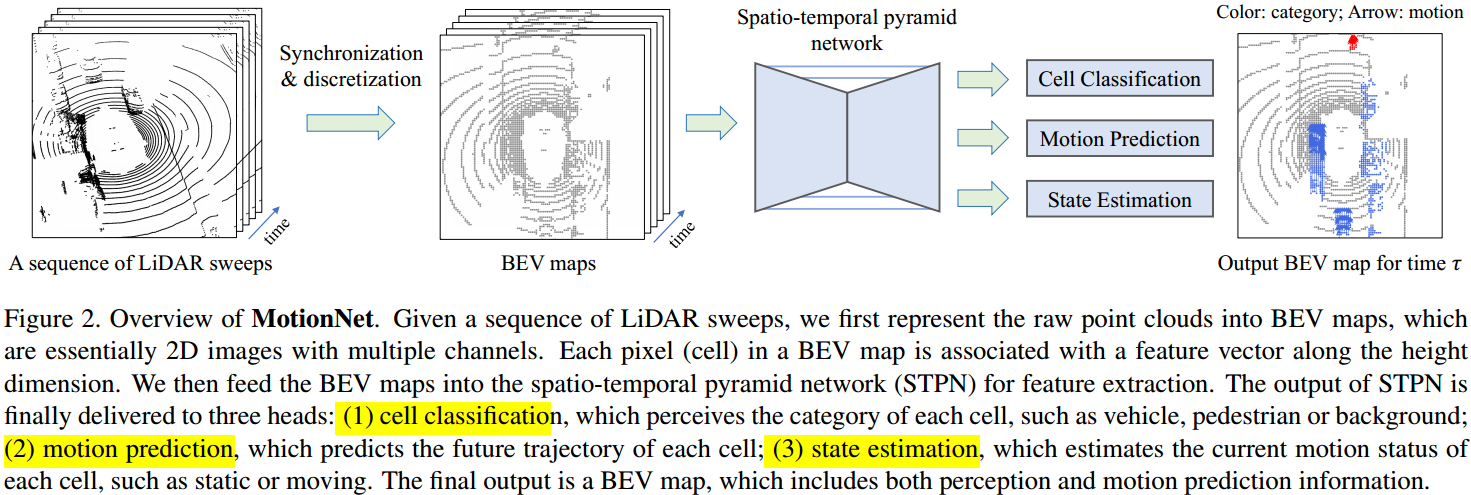如图 2. 所示，MotionNet 输入为连续帧点云在当前坐标系下的俯视图表示，然后经过 Spatio-temporal Pyramid 网络作特征提取，最后三个分支网络输出三个信息：
- Cell Classification，每个 cell 的类别；
- Motion Prediction，每个 cell 的未来轨迹；
- State Estimation，每个 cell 是否静止的判断；
2. Spatio-temporal Pyramid Network
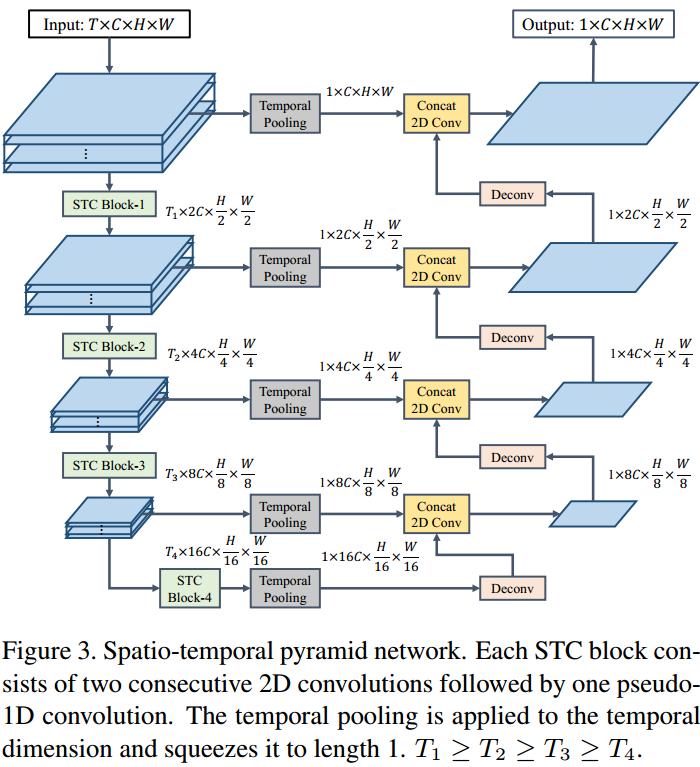将时序点云组织成多层的俯视图表达后，面临两个问题：1. 如何整合时序信息；2. 如何提取多尺度的空间及时序特征。本文设计了 STPN 网络，如图 3. 所示，STC 模块由 2D Convolution 以及 \(k\times 1\times 1\) 的 3D Convolution (本质上退化成 1D Convolution)组成；此外设计了金字塔式的特征提取结构，最终输出 \(1\times C\times H\times W\) 大小的特征图。相比于直接 3D 卷积形式，这种方式 2D + 1D 卷积方式极大提高了网络计算效率(很多地方用到这种方式，如 FaF)。
3. Output Heads
三个分支输出的细节为：
- Cell Classification，输出尺寸为 \(H\times W\times C\)，其中 \(C\) 为类别；
- Motion Prediction，输出尺寸为 \(N\times H\times W\times 2\)，表示时间 \(\tau\in (t,t+N)\) 内 cell 的位置 \(\{X ^ {(\tau)}\} _ {\tau =t} ^ {t + N}\)，其中 \(X ^ {(\tau)}\in\mathbb{R} ^ {H\times W\times 2}\) 只估计平面 2D 的位置。
- State Estimation，输出尺寸为 \(H\times W\)，表示 cell 静止的概率。
直接对静止 Cell 的 Motion Prediction 回归，会引入运动的微小跳变。这里采用两种策略来抑制这种跳变：1. 根据类别分支，如果是背景的类别，则将其 Motion 置 0；2. 根据静止判断分支，如果是静止的，则将其 Motion 也置为 0。这样就能较好的解决静态 cell 出速度轨迹的情况。
4. Loss Function
Classification 和 State Estimation 用 Cross-Entropy Loss，Motion Prediction 用 Smooth L1 Loss。此外为了保证空域与时域的一致性，引入另外三种 Loss：
- Spatial Consistency Loss
属于同一物体的 Cell 的 Motion 应该是一致的(这里其实不太准确，考虑到转向情况，目标区域内 Cell 轨迹其实是不一样的，所以一般有两种思路，一种认为都一样，即每个 Cell 都建模成目标的运动；另一种则基于刚体假设，作类似 Flow 的建模，稍复杂些)。由此设计空间一致性损失函数： \[L _ s = \sum _ {k}\sum _ {(i,j),(i',j')\in o _ k}\left\Vert X _ {i,j}^{(\tau)}-X _ {i',j'} ^ {(\tau)}\right\Vert \tag{1}\] 其中 \(||\cdot||\) 为 Smooth L1 Loss，\(o _ k\) 为第 \(k\) 个目标，\(X _ {i,j} ^ {(\tau)}\in\mathbb{R} ^ 2\) 为时间 \(\tau\) 时 Cell \((i,j)\) 的 motion。为了减少计算量，这里只是采样一些相邻的 \(X _ {i,j} ^ {(\tau)},X _ {i',j'} ^ {(\tau)}\) 匹配对。 - Foreground Temporal Consistency Loss
类似的，属于同一物体的 Motion 在时域上也应该是一致的，所以设计损失函数： \[L _ {ft} = \sum _ k\left\Vert X _ {o _ k} ^ {(\tau)} - X _ {o _ k} ^ {(\tau+\Delta t)}\right\Vert\tag{2}\] 其中 \(X _ {o _ k} ^ {(\tau)}\in\mathbb{R} ^ 2\) 为第 \(k\) 个目标的 Motion，计算方式为 \(X _ {o _ k} ^ {(\tau)}=\sum _ {(i,j)\in o _ k}X _ {i,j} ^ {(\tau)}/M\)，其中 \(M\) 为目标中 Cell 的个数。 - Background Temporal Consistency Loss
对静止的背景区域，其时域上 Motion 应该也是一致的(均为 0)。设计损失函数： \[L _ {bt} = \sum _ {(i,j)\;\in\; X ^ {(\tau)}\;\cap\; T\left(\tilde{X} ^ {(\tau-\Delta t)}\right)}\left\Vert X _ {i,j} ^ {(\tau)}-T _ {i,j}\left(\tilde{X} ^ {(\tau-\Delta t)}\right)\right\Vert\tag{3}\] 其中 \(T\in SE(3)\) 是 \(\tau-\Delta t\) 到 \(\tau\) 的位姿变换。将 \(\tilde{X} ^ {\tau-\Delta t}\) 变换到当前时刻后，与 \(X ^ {(\tau)}\) 会有一定的重合，将重合部分的背景区域的 Motion 约束为一致。有点 Grid-Mapping 的味道。
综上，所有的 Loss 为： \[ L = L _ {cls} + L _ {motion} + L _ {state} + \alpha L _ s+ \beta L _ {ft} + \gamma L _ {bt} \tag{4}\]
5. Reference
[1] Wu, Pengxiang, Siheng Chen, and Dimitris N. Metaxas. "MotionNet: Joint Perception and Motion Prediction for Autonomous Driving Based on Bird's Eye View Maps." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020.
