深度学习网络中的不确定性(Uncertainty)是一个比较重要的问题，本文[1]讨论了其中一种不确定性在多任务训练中的应用。目前关于深度学习不确定性的研究基本出自本文作者及其团队，后续我会较系统得整理其研究成果，这篇文章先只讨论一个较为实用的应用。
1. 不确定性概述
在贝叶斯模型中，可以建模两类不确定性[2]：
认知不确定性(Epistemic Uncertainty)，描述模型因为缺少训练数据而存在的未知，可通过增加训练数据解决；
偶然不确定性(Aleatoric Uncertainty)，描述了数据不能解释的信息，可通过提高数据的精度来消除；
- 数据依赖地或异方差不确定性(Data-dependent or Heteroscedastic Uncertainty)，与模型输入数据有关，可作为模型预测输出；
- 任务依赖地或同方差不确定性(Task-dependent or Homoscedastic Uncertainty)，与模型输入数据无关，且不是模型的预测输出，不同任务有不同的值；
本文讨论同方差不确定性，其描述了不同任务间的相关置信度，所以可用同方差不确定性来设计不同任务的 \(Loss\) 权重项。
2. 为什么需要设计不同任务的 \(Loss\) 权重项
如图 1. 所示，多任务学习能提高单任务的性能，但是要充分发挥多任务的性能，那么得精心调节各任务的 \(Loss\) 权重。当任务多的时候，人工搜索最优的权重项则显得费时费力，依靠模型的同方差不确定性，我们可以自动学习权重项。
3. 多任务似然建模
下面推倒基于同方差不确定性的最大化高斯似然过程。设模型权重 \(\mathbf{W}\)，输入 \(\mathbf{x}\)，输出为 \(\mathbf{f^W(x)}\)。对于回归任务，定义模型输出为高斯似然形式： \[p\left(\mathbf{y}\vert\mathbf{f^W(x)}\right) = \mathcal{N}\left(\mathbf{f^W(x)}, \sigma ^2\right) \tag{1}\] 其中 \(\sigma\) 为观测噪声方差，描述了模型输出中含有多大的噪声。对于分类任务，玻尔兹曼分布下的模型输出概率分布为： \[p\left(\mathbf{y}\vert\mathbf{f^W(x)},\sigma\right) = \mathrm{Softmax}\left(\frac{1}{\sigma ^2}\mathbf{f^W(x)}\right) \tag{2}\] 由此对于多任务，模型输出的联合概率分布为： \[p\left(\mathbf{y}_1,\dots,\mathbf{y}_K\vert\mathbf{f^W(x)}\right) = p\left(\mathbf{y}_1\vert\mathbf{f^W(x)}\right) \dots p\left(\mathbf{y}_K\vert\mathbf{f^W(x)}\right) \tag{3}\]
对于回归任务，\(log\)似然函数： \[\mathrm{log}p\left(\mathbf{y}\vert\mathbf{f^W(x)}\right) \propto -\frac{1}{2\sigma ^2} \Vert \mathbf{y-f^W(x)} \Vert ^2 - \mathrm{log}\sigma \tag{4}\] 对于分类任务，\(log\)似然函数： \[\mathrm{log}p\left(\mathbf{y}=c\vert\mathbf{f^W(x)}, \sigma\right) = \frac{1}{2\sigma ^2}f_c^{\mathbf{W}}(\mathbf{x})- \mathrm{log}\sum_{c'} \mathrm{exp}\left(\frac{1}{\sigma^2}f^{\mathbf{W}}_{c'}(\mathbf{x}) \right) \tag{5}\]
现同时考虑回归与分类任务，则多任务的联合 \(Loss\)： \[\begin{align} \mathcal{L}(\mathbf{W}, \sigma _1, \sigma _2) &= -\mathrm{log}p\left(\mathrm{y_1,y_2}=c\vert\mathbf{f^W(x)} \right) \\ &= -\mathrm{log}\mathcal{N}\left(\mathbf{y_1};\mathbf{f^W(x)}, \sigma_1^2\right) \cdot \mathrm{Softmax}\left(\mathbf{y_2}=c;\mathbf{f^W(x)},\sigma_2\right) \\ &= \frac{1}{2\sigma_1^2}\Vert \mathbf{y}_1-\mathbf{f^W(x)}\Vert ^2 + \mathrm{log}\sigma_1 - \mathrm{log}p\left(\mathbf{y}_2=c\vert\mathbf{f^W(x)},\sigma_2\right) \\ &= \frac{1}{2\sigma_1^2}\mathcal{L}_1(\mathbf{W}) +\frac{1}{\sigma_2^2}\mathcal{L}_2(\mathbf{W}) + \mathrm{log}\sigma_1 + \mathrm{log}\frac{\sum_{c'}\mathrm{exp}\left(\frac{1}{\sigma_2^2}f_{c'}^{\mathbf{W}}(x)\right)}{\left(\sum_{c'}\mathrm{exp}\left(f_{c'}^{\mathbf{W}}(x) \right) \right)^{\frac{1}{\sigma_2^2}}} \\ &\approx \frac{1}{2\sigma_1^2}\mathcal{L}_1(\mathbf{W}) +\frac{1}{\sigma_2^2}\mathcal{L}_2(\mathbf{W}) + \mathrm{log}\sigma_1 + \mathrm{log}\sigma_2 \tag{6} \end{align}\]
由此得到两个权重项，任务噪声 \(\sigma\) 越大，则该任务的误差权重越小。实际应用中，为了数值稳定，令 \(s:=\mathrm{log}\sigma^2\): \[\mathcal{L}(\mathbf{W}, s_1, s_2) = \frac{1}{2}\mathrm{exp}(-s_1)\mathcal{L}_1(\mathbf{W}) + \mathrm{exp}(-s_2)\mathcal{L}_2(\mathbf{W}) + \mathrm{exp}(\frac{1}{2}s_1) + \mathrm{exp}(\frac{1}{2}s_2) \tag{7}\] 对于更多任务的模型，根据任务类型也很容易扩展，网络自动学习权重项 \((s_1,s_2,...,s_n)\)。
4. 实验结果
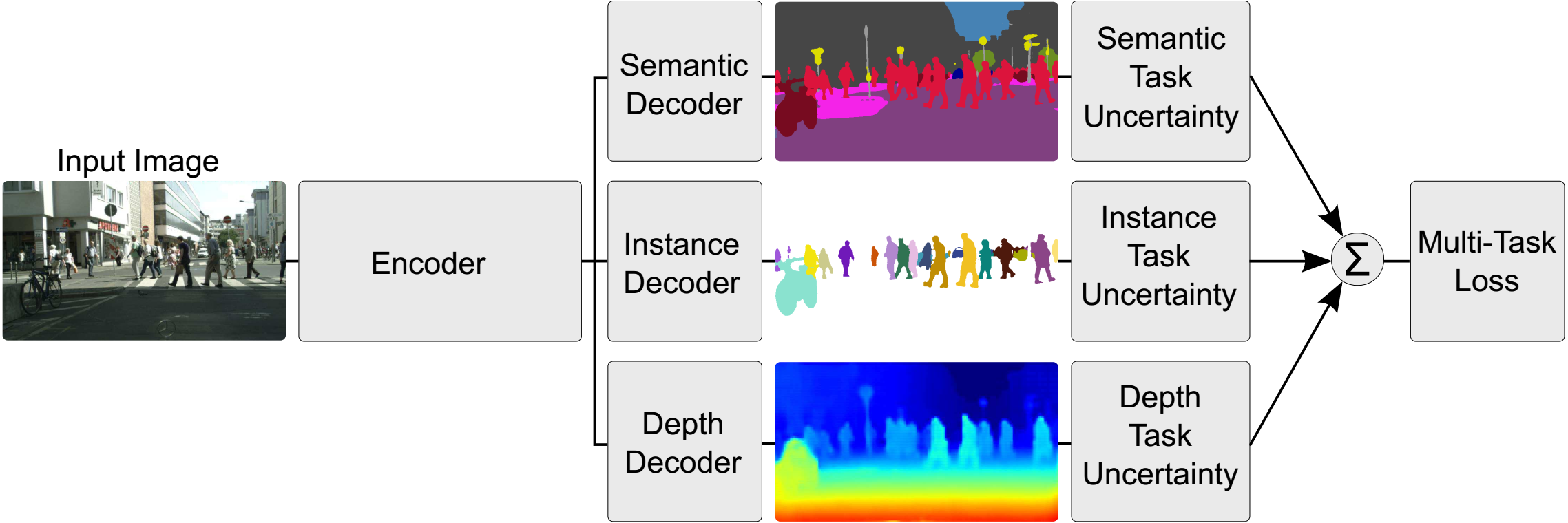
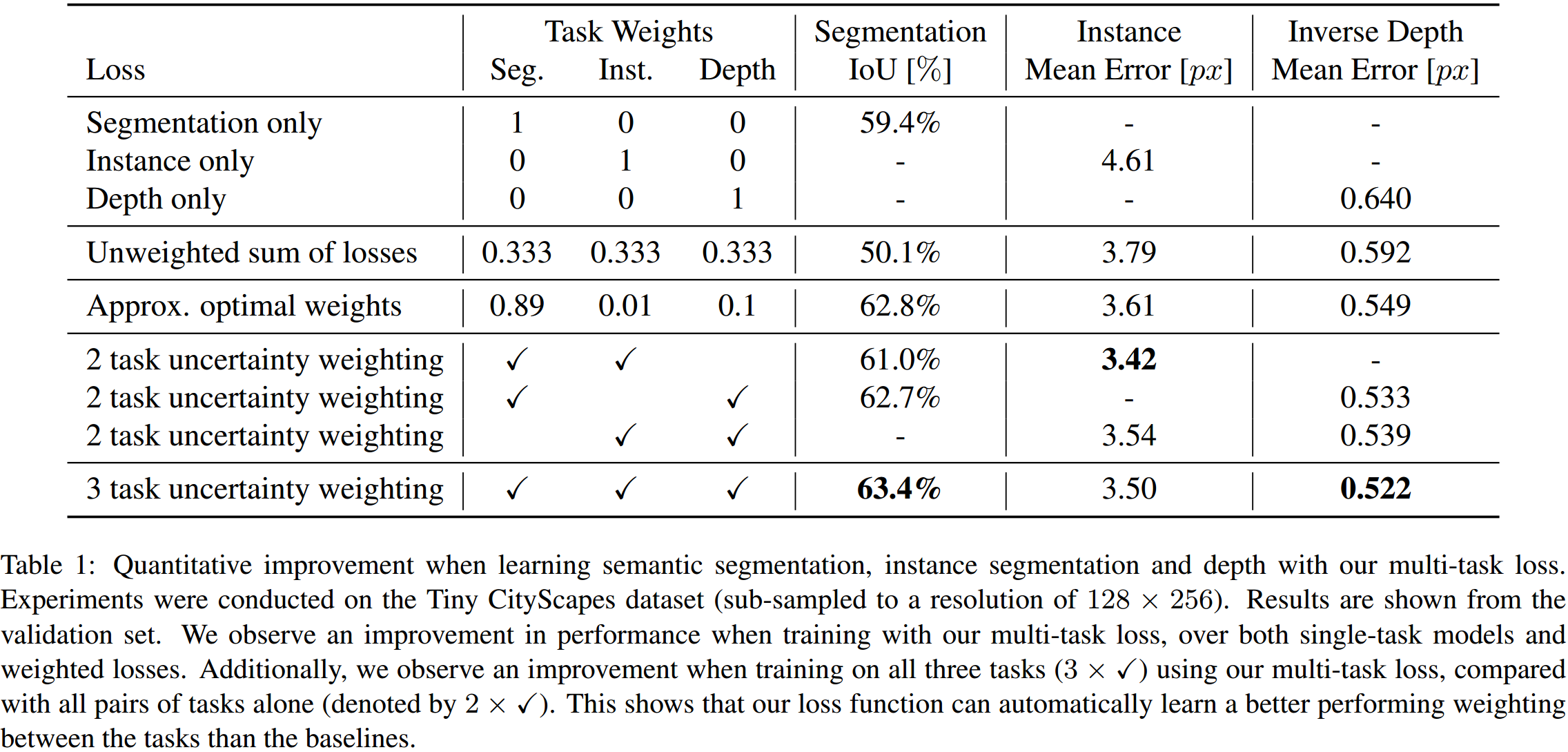如图 2. 所示，作者设计了同时作语义分割、实例分割、深度估计的网络，由图 3. 可知，用任务的不确定性来加权任务的 \(Loss\)，效果显著。
5. 参考文献
[1] Kendall, Alex, Yarin Gal, and Roberto Cipolla. "Multi-task learning using uncertainty to weigh losses for scene geometry and semantics." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018.
[2] Kendall, Alex, and Yarin Gal. "What uncertainties do we need in bayesian deep learning for computer vision?." Advances in neural information processing systems. 2017.
