模型压缩技术主要有：Pruning，Regularization，Quantization，KnowLedge Distillation，Comditional Computation等。本文主要讨论剪枝技术(Pruning)。复杂模型存在存储空间大，计算量大等问题，对其进行剪枝使网络中的权重及特征层稀疏化(Regularization 也是稀疏化的过程)，能获得以下效益：
- 模型更小
稀疏化的模型含有大量的零值，称为稀疏表达(Sparse Representation)，通过稀疏矩阵压缩技术进行编码压缩后得到压缩表达(Compressed Representation)。片内内存(On-chip Mem)与片外内存(Off-chip Mem)数据的传输可用压缩表达，使实际传输中的模型内存更小，而计算时，可通过反编码算法得到稀疏表达，从而进行正常的矩阵运算；也可以直接用压缩表达进行矩阵运算，这需要特殊的硬件支持，并且稀疏化的过程一般是结构化剪枝(Structured Pruning)或是正则。 - 速度更快
目前大部分矩阵运算芯片，性能瓶颈都在片内片外内存的带宽，稀疏化后能有效压缩矩阵单元，降低模型传输内存；另一方面，通过结构化的剪枝，在特定硬件下，能直接减少零值运算量。 - 能效更高
片外内存访问所花费的能量大概比片内内存多两个数量级，所以降低模型的传输内存，甚至将模型及中间计算量(如特征层)直接塞到片内内存，减少与片外内存的交互，能有效提高能效。
剪枝的过程主要是：根据剪枝类型选用对应的稀疏性定义方式；剪枝前模型的敏感度分析；应用剪枝算法及策略。以下根据 Distiller[1] 库分别对这三部分进行详细阐述。
1. 稀疏性定义
剪枝大致可分为 element-wise 剪枝以及 Structured 剪枝，element-wise 剪枝只需要定义每个张量的稀疏性，即 Element-wise Sparsity，而 Structured 剪枝需要定义不同结构的稀疏性，有 Filter-wise Sparsity，Channel-wise Sparsity，Kernel-wise Sparsity，Block-wise Sparsity，Column-wise Sparsity，Row-wise Sparsity。
设输入特征层 IFM(Input Feature Map)\(\in\mathbb{R}^{N\times C_1\times H_1\times W_1}\)，卷积核 Filter\(\in\mathbb{R}^{C_2\times C_1\times K\times K}\)，则输出特征层 OFM(Output Feature Map)\(\in\mathbb{R}^{N\times C_2\times H_2\times W_2}\)。
1.1. Element-wise Sparsity
张量元素的稀疏性，设 \(X\in\mathbb{R}^{N\times C\times H\times W}\)： \[\Vert X\Vert_{element-wise} = \frac{l_0(X)}{N\times C\times H\times W} = \frac{\sum_{n=1}^{N}\sum_{c=1}^{C}\sum_{h=1}^{H}\sum_{w=1}^{W}\left\vert X_{n,c,h,w} \right\vert ^0}{N\times C\times H\times W} \tag{1}\] 其中 \(l_0\) 正则根据元素是否为 0，确定输出 0/1。
1.2. Filter-wise Sparsity
对于有 \(C_2\) 个卷积核的 Filter\(\in\mathbb{R}^{C_2\times C_1\times K\times K}\)，其 Filter-wise 的稀疏性可表示为： \[\Vert X\Vert_{filter-wise} = \frac{\sum_{c_2=1}^{C_2}\left\vert\sum_{c_1=1}^{C_1}\sum_{k_1=1}^{K}\sum_{k_2=1}^{K}\vert X_{c_2,c_1,k_1,k_2}\vert \right\vert ^0}{C_2} \tag{2}\]
1.3. Kernel-wise Sparsity
卷积核 Filter\(\in\mathbb{R}^{C_2\times C_1\times K\times K}\) 拥有 \(C_2\times C_1\) 个 \(K\times K\) 大小的 Kernel，其 Kernel-wise 的稀疏性可表示为： \[\Vert X\Vert_{kernel-wise} = \frac{\sum_{c_2=1}^{C_2}\sum_{c_1=1}^{C_1}\left\vert\sum_{k_1=1}^{K}\sum_{k_2=1}^{K}\vert X_{c_2,c_1,k_1,k_2}\vert \right\vert ^0}{C_2\times C_1} \tag{3}\]
1.4. Channel-wise Sparsity
对于张量单元 \(X\in\mathbb{R}^{N\times C\times H\times W}\)： \[\Vert X\Vert_{channel-wise} = \frac{\sum_{c=1}^{C}\left\vert\sum_{n=1}^{N}\sum_{h=1}^{H}\sum_{w=1}^{W}\vert X_{n,c,h,w}\vert \right\vert ^0}{C} \tag{4}\]
1.5. Column-wise Sparsity
对于张量单元 \(X\in\mathbb{R}^{H\times W}\)： \[\Vert X\Vert_{column-wise} = \frac{\sum_{h=1}^{H}\left\vert\sum_{w=1}^{W}\vert X_{h,w}\vert \right\vert ^0}{H} \tag{5}\]
1.6. Row-wise Sparsity。
对于张量单元 \(X\in\mathbb{R}^{H\times W}\)： \[\Vert X\Vert_{row-wise} = \frac{\sum_{w=1}^{W}\left\vert\sum_{h=1}^{H}\vert X_{h,w}\vert \right\vert ^0}{W} \tag{6}\]
1.7. Block-wise Sparsity
对于张量单元 \(X\in\mathbb{R}^{N\times C\times H\times W}\)，设定 block\(\in\mathbb{R}^{repetitions\times depth\times 1\times1}\)，由此将 \(X\) 划分为 \(\frac{N\times C}{repetitions\times depth}\times (repetitions\times depth)\times (H\times W)=N'\times B\times K\)。block-sparsity 定义为： \[\Vert X\Vert_{block-wise} = \frac{\sum_{n=1}^{N'}\sum_{k=1}^K\left\vert\sum_{b=1}^{B}\vert X_{n,b,k}\vert \right\vert ^0}{N'\times K} \tag{7}\]
2. 模型敏感度分析(Sensitivity Analysis)
在剪枝前，我们首先要确定减哪几层，每层减多少(即剪枝阈值或剪枝程度)。这就涉及到模型中每层网络对模型输出的敏感度分析(Sensitivity Analysis)。[2] 提出了一种有效的方法来确定每层的敏感度。在一个已训练模型下，分别对每一层进行不同程度的剪枝，得到对应的网络输出精度，绘制敏感度曲线。
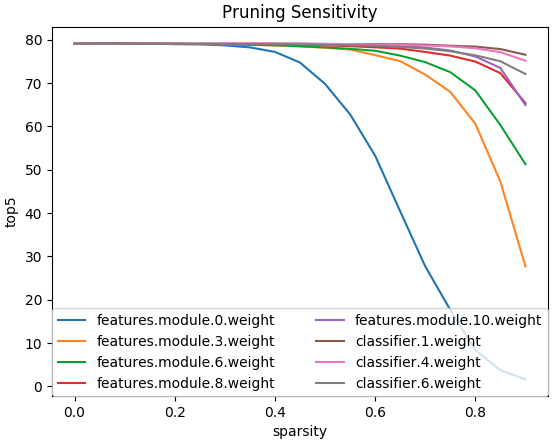如图 1. 所示，AlexNet 网络各层对 element-wise 剪枝的敏感度曲线显示，越深的网络层对输出越不敏感，尤其是全连接层，所以剪枝程度可以更高。而对于非常敏感的浅层网络，则需要降低剪枝程度，甚至不剪枝。
3. 剪枝算法
3.1. Magnitude Pruner
这是最基本的剪枝方法，对于要剪枝的对象，判断其绝对值是否大于阈值 \(\lambda\)，如果小于阈值，则将该对象置为零。该对象可以是 element-wise，也可以是其它结构化的对象，如 filter，Kernel 等。
该方法需要直接设定阈值，而阈值的设定是比较困难的。
3.2. Sensitivity Pruner
卷积网络每层的权重值为高斯分布，由高斯分布的性质可知，在标准差 \(\sigma\) 内，有 68% 的元素，所以阈值可设定为 \(\lambda=s\times \sigma\)，其表示了 \(s\times 68\%\) 的元素被剪枝掉。
3.3. Level Pruner
Level Pruner 直接设定需要剪枝的比例，即直接设定剪枝后的稀疏性，这比前两种方法更加稳定。具体做法就是对每个对象进行排序，然后以此裁剪，直到裁剪到设定的比例。
3.4. Automated Gradual Pruner(AGP)
[3]提出了一种训练剪枝的方法，在 Level Pruner 基础上，随着训练的过程，设计剪枝的稀疏性从初始的 \(s_i\) 增加到目标 \(s_f\)，其数学表示为： \[ s_t = s_f+(s_i-s_f)\left(1-\frac{t-t_0}{n\Delta t}\right)^3 \; \mathrm{for} \, t\in \{t_0, t_0+\Delta t,...,t_0+n\Delta t\} \tag{8}\] 实现的效果是，初始阶段，剪枝比较厉害，越到最后，剪枝的量越少，直到达到目标剪枝值。
3.5. Structure Pruners
这里讨论结构化剪枝中 Filter 以及 Channel 的剪枝[4]，对应的需要用到前面提到的 Filter-wise 以及 Channel-wise 的稀疏性。不同于 element-wise 剪枝，结构化剪枝由于网络的连接性会更复杂，这里考虑三种链接情况。
3.5.1. 连接结构1
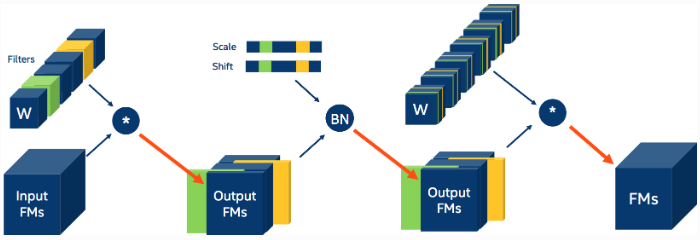如图 2. 所示，设第\(i\)层特征 \(X_i\in\mathbb{R}^{C_i\times H_i\times W_i}\)，经过卷积核 \(\mathcal{F}\in\mathbb{R}^{C_{i+1}\,\times\, C_i\,\times\,K\,\times\,K}\)后得到第 \(i+1\)层特征层 \(X_{i+1}\in\mathbb{R}^{C_{i+1}\,\times\, H_{i+1}\,\times\, W_{i+1}}\)。图中绿色及黄色代表剪枝掉的 Filter，对应的输出少了这两个卷积计算得到的 channel 维度的两个特征图，再往后就是去除 BN 里面对应 channel 层的 scale 以及 shift 信息(Distiller 中自动删除)，最后再次应用的卷积核需要去除对应的 channel，即类似做 channel-wise 剪枝。由此可见，结构化剪枝会影响后面的网络结构，需要根据网络信息流作网络调整。
第 \(i\) 卷积层运算量 MAC 为 \(C_{i+1}C_iK^2H_{i+1}W_{i+1}\)，如果剪枝掉 \(m\) 个卷积核，那么第 i 层卷积减少的运算量为 \(mC_iK^2H_{i+1}W_{i+1}\)，下一层 \(i+1\) 卷积层减少的运算量为 \(C_{i+2}mK^2H_{i+2}W_{i+2}\)。所以在第 \(i\) 层剪枝掉 \(m\) 个卷积核，会使第 \(i,i+1\) 层的运算量各减少 \(m/C_{i+1}\)。
3.5.2. 连接结构2
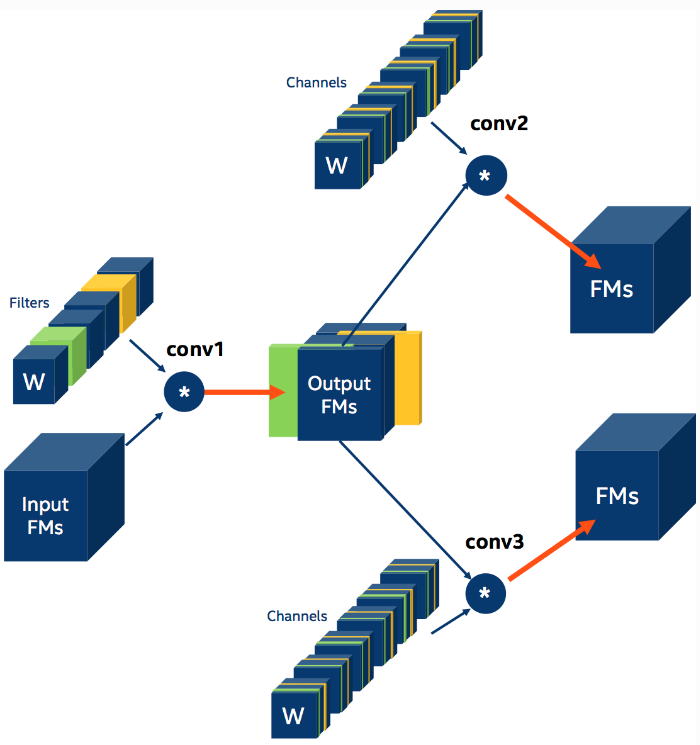如图 3. 所示，与被剪枝的特征图直连的卷积核均需要作 channel 维度的裁剪，这一步在 Distiller 中自动进行。
3.5.3. 连接结构3
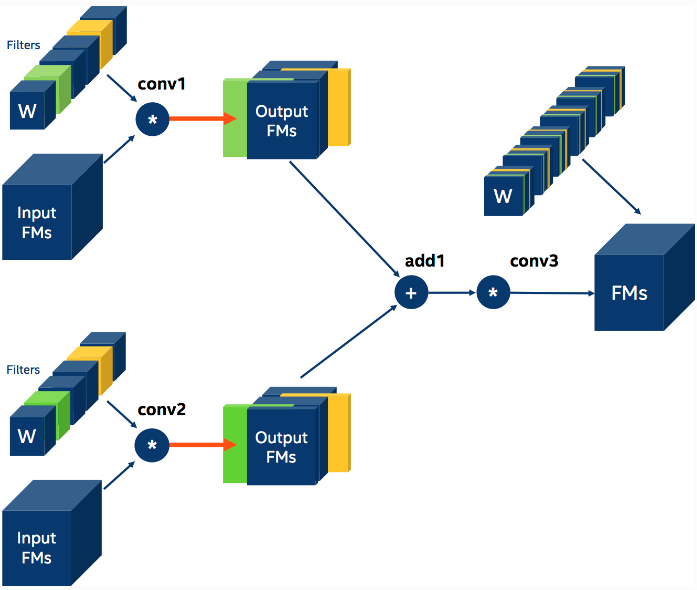如图 4. 所示，如果两个卷积层的输出要做 element-wise 相加操作，那么就要求两个卷积层的输出大小要一样。这就要求对这两个卷积层的卷积核裁剪过程要一样，包括裁剪的卷积数量以及卷积位置。这需要在 Distiller 中显示的指定。
4. 参考文献
[1] https://nervanasystems.github.io/distiller/index.html
[2] Han, Song, et al. "Learning both weights and connections for efficient neural network." Advances in neural information processing systems. 2015.
[3] Zhu, Michael, and Suyog Gupta. "To prune, or not to prune: exploring the efficacy of pruning for model compression." arXiv preprint arXiv:1710.01878 (2017).
[4] Li, Hao, et al. "Pruning filters for efficient convnets." arXiv preprint arXiv:1608.08710 (2016).
