目前主流的三维目标的状态估计方法（也可称为 MOT 问题）主要包括三部分：1. 检测，出单帧三维目标信息；2. 跟踪，前后帧数据关联出 ID 信息；3. 滤波，平滑估计状态信息。这里的“跟踪”只是狭义地指出 ID 的过程，“滤波”也就是综述 Multiple-Object-Tracking-A-Literature-Review 中提到的 Inference 过程。Inference 过程还可以是基于优化的方法，本文我们主要讨论在自动驾驶中估计动态障碍物状态的扩展卡尔曼滤波方法。
1. 扩展卡尔曼滤波
文章卡尔曼滤波详解中已经详细推导了卡尔曼滤波相关原理，这里摘抄如下。非线性系统： \[\left\{\begin{array}{l} 运动方程:\quad x_k=f(x_{k-1},u_k)+w_k \\ 测量方程:\quad z_k=h(x_k)+v_k \end{array}\tag{1}\right.\] 滤波的两个步骤：
- 预测（Predict）
计算先验： \[\begin{align} \bar{x} _k&=f(\hat{x} _{k-1},u _k) \tag{2}\\ \bar{P} _k&=F\hat{P} _kF^T+Q _k \tag{3} \end{align}\] - 更新（Update）
先计算卡尔曼增益： \[K_k=\bar{P}_kH_k^T(H_k\bar{P}_kH_k^T+R_k)^{-1} \tag{4}\] 再计算后验概率分布： \[\begin{align} \hat{x}_k &=\bar{x}_k+K(z_k-h(\bar{x})) \tag{5}\\ \hat{P}_k &=(I-KH_k)\bar{P}_k \tag{6} \end{align}\]
2. 非线性系统构建
要构建三维目标状态估计系统，我们得分析状态量 \(x_k\)，测量量 \(z_k\)，输入量 \(u_k\)，状态转移函数（运动学方程）\(f(\cdot)\)，观测函数 \(h(\cdot)\)，以及雅克比矩阵 \(F\)，\(H\) 各是什么。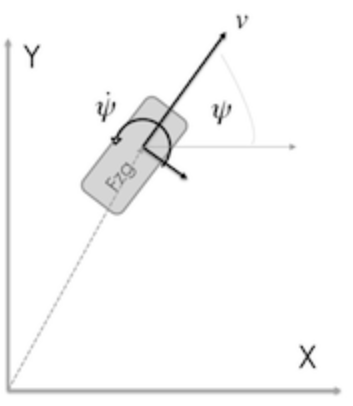 
如图1所示，我们严格限定要构建的非线性系统场景：动态目标的状态估计。对于自动驾驶中的动态目标状态估计，我们关心的状态量有水平面上目标物理位置，朝向，速度，转向速度，加速度，记为： \[x_k=\begin{bmatrix}
x\\
y\\
\psi\\
v\\
\dot{\psi}\\
a\end{bmatrix}\tag{7}\] 目前主流的 3D 检测方法，能出位置，尺寸，朝向。所以测量量： \[z_k=\begin{bmatrix}
x\\
y\\
\psi\\
\end{bmatrix}\tag{8}\] 以上针对的是目标三维状态估计，如果是本车的状态估计，那么测量量可能可以加上本车的速度等（故限定场景）。文章 [paper_reading]-"Stereo Vision-based Semantic 3D Object and Ego-motion Tracking for Autonomous Driving" 的 3.2.1 章节中提到过一种车辆运动学模型，该模型定义了输入量：方向盘比率以及加速度（实际使用中均设为0，类似下述质点模型中的 CTRV 模型）；并增加了状态量：方向盘转角。虽然那篇文章处理的场景与本篇讨论的一致，但是那篇文章采用的是优化方法，方向盘转角可作为优化参数进行求解；而本篇讨论的滤波迭代方法，则很难确定方向盘转角。所以该模型虽然能更好的描述目标，但是可能并不是更有效的（实际中可做实验对比），这里引出几种质点模型。
[1]中介绍了几种非线性车辆质点模型：CHCV(Constant Heading and Constant Velocity)，CTRV(Constant Turn Rate and Velocity)，CTRA(Constant Turn Rate and Acceleration)，此外应该还有 CHA(Constant Heading and Acceleration)。这些模型均没有考虑输入量，即： \[u_k=\mathbb{0}\tag{9}\] 这里我们依次介绍各模型（为了完整性，重写文章 [paper_reading]-"Stereo Vision-based Semantic 3D Object and Ego-motion Tracking for Autonomous Driving" 中的前转向车运动学模型），并导出状态转移函数（运动学方程）\(f(\cdot)\)，观测函数 \(h(\cdot)\)，以及雅克比矩阵 \(F\)，\(H\)。
2.1. CHCV(Constant Heading and Constant Velocity)
该模型下，目标车辆的朝向及速度不变，即 \(\dot{\psi}=0\)。则容易写出，在时间 \(\Delta T\) 内，运动方程\(f(\cdot)\)为： \[\begin{align} & \begin{bmatrix} x\\ y\\ \psi\\ v\\ \dot{\psi}\end{bmatrix} _k= \begin{bmatrix} x+v\,cos(\psi)\Delta T\\ y+v\,sin(\psi)\Delta T\\ \psi\\ v\\ 0\end{bmatrix} _{k-1} \\ \iff &\begin{bmatrix} x\\ y\\ \psi\\ v\\ \end{bmatrix} _k= \begin{bmatrix} x+v\,cos(\psi)\Delta T\\ y+v\,sin(\psi)\Delta T\\ \psi\\ v\\ \end{bmatrix} _{k-1} \tag{10} \end{align}\] 观测方程\(h(\cdot)\)也可得到： \[\begin{bmatrix} x\\ y\\ \psi\\ \end{bmatrix} _k= \begin{bmatrix} 1 &0 &0 &0\\ 0 &1 &0 &0\\ 0 &0 &1 &0\\ \end{bmatrix} \begin{bmatrix} x\\ y\\ \psi\\ v\\ \end{bmatrix} _{k} \tag{11} \] 由此得到雅克比矩阵： \[\begin{align}F&= \begin{bmatrix} 1 &0 &-v\,sin(\psi)\Delta T &cos(\psi)\Delta T\\ 0 &1 &v\,cos(\psi)\Delta T &sin(\psi)\Delta T\\ 0 &0 &1 &0\\ 0 &0 &0 &1 \end{bmatrix} \tag{12} \\ H&=\begin{bmatrix} 1 &0 &0 &0\\ 0 &1 &0 &0\\ 0 &0 &1 &0\\ \end{bmatrix} \tag{13} \end{align}\]
2.2. CTRV(Constant Turn Rate and Velocity)
该模型下，目标车辆的(朝向)转向速度及线速度不变，即 \(a=0\)。则分别在 \(x,y\) 方向上，位移积分为： \[\left\{\begin{array}{l} x=\int_0^{\Delta T} v\,cos(\dot{\psi}t+\psi)dt=\frac{v}{\dot{\psi}}sin(\dot{\psi}t+\psi)\vert_0^{\Delta T}&= \frac{v}{\dot{\psi}}(sin(\dot{\psi}\Delta T+\psi)-sin(\psi)) \\ y=\int_0^{\Delta T} v\,sin(\dot{\psi}t+\psi)dt=-\frac{v}{\dot{\psi}}cos(\dot{\psi}t+\psi)\vert_0^{\Delta T}&=\frac{v}{\dot{\psi}}(cos(\psi)-cos(\dot{\psi}\Delta T+\psi)) \\ \end{array}\tag{14}\right.\] 由此得到运动方程\(f(\cdot)\)为： \[\begin{bmatrix} x\\ y\\ \psi\\ v\\ \dot{\psi}\end{bmatrix} _k= \begin{bmatrix} x+\frac{v}{\dot{\psi}}(sin(\dot{\psi}\Delta T+\psi)-sin(\psi))\\ y+\frac{v}{\dot{\psi}}(cos(\psi)-cos(\dot{\psi}\Delta T+\psi)) \\ \psi+\dot{\psi}\Delta T\\ v\\ \dot{\psi}\end{bmatrix} _{k-1} \tag{15} \] 观测方程则还是线性方程： \[\begin{bmatrix} x\\ y\\ \psi\\ \end{bmatrix} _k= \begin{bmatrix} 1 &0 &0 &0 &0\\ 0 &1 &0 &0 &0\\ 0 &0 &1 &0 &0\\ \end{bmatrix} \begin{bmatrix} x\\ y\\ \psi\\ v\\ \dot{\psi} \end{bmatrix} _{k} \tag{16} \] 由此得到雅克比矩阵： \[\begin{align}F&= \begin{bmatrix} 1 &0 &\frac{v}{\dot{\psi}}(cos(\dot{\psi}+\psi)-cos(\psi)) &\frac{1}{\dot{\psi}}(sin(\dot{\psi}\Delta T+\psi)-sin(\psi)) &\frac{v\Delta T}{\dot{\psi}}cos(\dot{\psi}\Delta T+\psi)-\frac{v}{\dot{\psi}^2}(sin(\dot{\psi}\Delta T+\psi)-sin(\psi)) \\ 0 &1 &\frac{v}{\dot{\psi}}(sin(\dot{\psi}+\psi)-sin(\psi)) &\frac{1}{\dot{\psi}}(cos(\psi)-cos(\dot{\psi}\Delta T+\psi)) &\frac{v\Delta T}{\dot{\psi}}sin(\dot{\psi}\Delta T+\psi)-\frac{v}{\dot{\psi}^2}(cos(\psi)-cos(\dot{\psi}\Delta T+\psi)) \\ 0 &0 &1 &0 &\Delta T\\ 0 &0 &0 &1 &0\\ 0 &0 &0 &0 &1\\ \end{bmatrix} \tag{17} \\ H&=\begin{bmatrix} 1 &0 &0 &0 &0\\ 0 &1 &0 &0 &0\\ 0 &0 &1 &0 &0\\ \end{bmatrix} \tag{18} \end{align}\]
2.3. CTRA(Constant Turn Rate and Acceleration)
该模型下，目标车辆的(朝向)转向速度及线加速度不变。\(x,y\) 方向上的位移积分为： \[\left\{\begin{array}{l} x&=&\int_0^{\Delta T} (v+at)\,cos(\dot{\psi}t+\psi)dt= \frac{a}{\dot{\psi}^2}cos(\dot{\psi}t+\psi)+\frac{v+at}{\dot{\psi}}sin(\dot{\psi}t+\psi)\vert_0^{\Delta T}\\ &=& \frac{a}{\dot{\psi}^2}cos(\dot{\psi}\Delta T+\psi)+\frac{v+a\Delta T}{\dot{\psi}}sin(\dot{\psi}\Delta T+\psi)-\frac{a}{\dot{\psi}^2}cos(\psi)-\frac{v}{\dot{\psi}}sin(\psi)\\ y&=&\int_0^{\Delta T} (v+at)\,sin(\dot{\psi}t+\psi)dt= \frac{a}{\dot{\psi}^2}sin(\dot{\psi}t+\psi)-\frac{v+at}{\dot{\psi}}cos(\dot{\psi}t+\psi)\vert_0^{\Delta T}\\ &=& \frac{a}{\dot{\psi}^2}sin(\dot{\psi}\Delta T+\psi)-\frac{v+a\Delta T}{\dot{\psi}}cos(\dot{\psi}\Delta T+\psi)-\frac{a}{\dot{\psi}^2}sin(\psi)+\frac{v}{\dot{\psi}}cos(\psi)\\ \end{array}\tag{19}\right.\] 由此得到运动方程\(f(\cdot)\)为： \[\begin{bmatrix} x\\ y\\ \psi\\ v\\ \dot{\psi}\\ a\end{bmatrix} _k= \begin{bmatrix} x+\frac{a}{\dot{\psi}^2}cos(\dot{\psi}\Delta T+\psi)+\frac{v+a\Delta T}{\dot{\psi}}sin(\dot{\psi}\Delta T+\psi)-\frac{a}{\dot{\psi}^2}cos(\psi)-\frac{v}{\dot{\psi}}sin(\psi)\\ y+\frac{a}{\dot{\psi}^2}sin(\dot{\psi}\Delta T+\psi)-\frac{v+a\Delta T}{\dot{\psi}}cos(\dot{\psi}\Delta T+\psi)-\frac{a}{\dot{\psi}^2}sin(\psi)+\frac{v}{\dot{\psi}}cos(\psi) \\ \psi+\dot{\psi}\Delta T\\ v+a\Delta T\\ \dot{\psi}\\ a\end{bmatrix} _{k-1} \tag{20} \] 观测方程则还是线性方程： \[\begin{bmatrix} x\\ y\\ \psi\\ \end{bmatrix} _k= \begin{bmatrix} 1 &0 &0 &0 &0 &0\\ 0 &1 &0 &0 &0 &0\\ 0 &0 &1 &0 &0 &0\\ \end{bmatrix} \begin{bmatrix} x\\ y\\ \psi\\ v\\ \dot{\psi}\\ a\end{bmatrix} _{k} \tag{21} \] 同理可得到雅克比矩阵，由于页面限制，这里不再写出。
2.4. CHA(Constant Heading and Acceleration)
该模型下，此时目标车辆的朝向及线加速度不变，即 \(\dot{\psi}=0\)。\(x,y\) 方向上的位移积分为： \[\left\{\begin{array}{l} x=\int_0^{\Delta T} (v+at)\,cos(\psi)dt= \left(vt+\frac{1}{2}at^2\right)cos(\psi)\vert_0^{\Delta T}&= \left(v\Delta T+\frac{1}{2}a\Delta T^2 \right)cos(\psi) \\ y=\int_0^{\Delta T} (v+at)\,sin(\psi)dt= \left(vt+\frac{1}{2}at^2\right)sin(\psi)\vert_0^{\Delta T}&= \left(v\Delta T+\frac{1}{2}a\Delta T^2 \right)sin(\psi) \\ \end{array}\tag{22}\right.\] 由此得到运动方程\(f(\cdot)\)为： \[\begin{bmatrix} x\\ y\\ \psi\\ v\\ a\end{bmatrix} _k= \begin{bmatrix} x+\left(v\Delta T+\frac{1}{2}a\Delta T^2 \right)cos(\psi)\\ y+\left(v\Delta T+\frac{1}{2}a\Delta T^2 \right)sin(\psi) \\ \psi\\ v+a\Delta T\\ a\end{bmatrix} _{k-1} \tag{23} \] 观测方程则还是线性方程： \[\begin{bmatrix} x\\ y\\ \psi\\ \end{bmatrix} _k= \begin{bmatrix} 1 &0 &0 &0 &0\\ 0 &1 &0 &0 &0\\ 0 &0 &1 &0 &0\\ \end{bmatrix} \begin{bmatrix} x\\ y\\ \psi\\ v\\ a\end{bmatrix} _{k} \tag{24} \] 由此得到雅克比矩阵： \[\begin{align}F&= \begin{bmatrix} 1 &0 &-\left(v\Delta T+\frac{1}{2}a\Delta T^2 \right)sin(\psi) &\Delta Tcos(\psi) &\frac{1}{2}\Delta T^2cos(\psi) \\ 0 &1 &\left(v\Delta T+\frac{1}{2}a\Delta T^2 \right)cos(\psi) &\Delta Tsin(\psi) &\frac{1}{2}\Delta T^2sin(\psi)\\ 0 &0 &1 &0 &0\\ 0 &0 &0 &1 &\Delta T \\ 0 &0 &0 &0 &1 \end{bmatrix} \tag{25} \\ H&=\begin{bmatrix} 1 &0 &0 &0 &0\\ 0 &1 &0 &0 &0\\ 0 &0 &1 &0 &0\\ \end{bmatrix} \tag{26} \end{align}\]
2.5. 前转向车模型
这里给出文章 [paper_reading]-"Stereo Vision-based Semantic 3D Object and Ego-motion Tracking for Autonomous Driving" 中的前转向车运动学模型，推导过程可见文章。这里令方向盘角度比率 \(\gamma\) 以及加速度 \(a\) 为 0，所以本质上也是个 CTRV 模型。
引入状态变量方向盘/车轮角度 \(\delta\)（与朝向转速 \(\psi\) 类似），运动方程\(f(\cdot)\)为： \[\begin{bmatrix}
x\\
y\\
\psi\\
v\\
\delta\end{bmatrix} _k=
\begin{bmatrix}
x+cos(\psi)v\Delta T\\
y+sin(\psi)v\Delta T \\
\psi+\frac{tan(\delta)}{L}v\Delta T\\
v\\
\delta\end{bmatrix} _{k-1} \tag{27}
\] 观测方程则还是线性方程： \[\begin{bmatrix}
x\\
y\\
\psi\\
\end{bmatrix} _k=
\begin{bmatrix}
1 &0 &0 &0 &0\\
0 &1 &0 &0 &0\\
0 &0 &1 &0 &0\\
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
\psi\\
v\\
\delta\end{bmatrix} _{k} \tag{28} \] 由此得到雅克比矩阵： \[\begin{align}F&=
\begin{bmatrix}
1 &0 &-sin(\psi)v\Delta T &cos(\psi)\Delta T &0 \\
0 &1 &cos(\psi)v\Delta T &sin(\psi)\Delta T &0 \\
0 &0 &1 &\frac{tan(\delta)}{L}\Delta T &\frac{v}{Lcos^2(\delta)}\Delta T\\
0 &0 &0 &1 &0\\
0 &0 &0 &0 &1\\
\end{bmatrix} \tag{29} \\
H&=\begin{bmatrix}
1 &0 &0 &0 &0\\
0 &1 &0 &0 &0\\
0 &0 &1 &0 &0\\
\end{bmatrix} \tag{30}
\end{align}\]
3. 状态及参数初始化
以上介绍了四个质点模型以及一个前转向模型，当然还有更复杂的模型，但是对于目标车辆的状态估计，由于观测量有限，而且也不能知道输入量（如果 V2X 能够实现，那就知道目标车辆的更多状态信息了），所以这些模型也基本够用。
模型构建好之后，为了迭代，还需初始化各个状态量及协方差参数矩阵。初始化值不对，会导致迭代发散，这里初始化就会有几个问题：
- 无法观测的状态量较难初始化，如转向速度，线加速度等；
- 观测不稳定的状态量较难初始化，如目标有截断的情况下；
- 协方差矩阵较难初始化，如状态量的协方差矩阵；
前两个问题需要在工程实践中优化；最后一个问题（非常重要）可以让检测网络同时出预测值的不确定性(Uncertainty)，这也是深度学习中一个较为系统性的工作，后面文章再做介绍。
[1] https://github.com/balzer82/Kalman
