LOAM(Lidar Odometry and Mapping)

Posted on   |   Updated on | In | 本文总阅读量 次
Words count in article: 4.2k 字 | Reading time ≈ 17 分钟

　　SLAM 是机器人领域非常重要的一个功能模块，而基于激光雷达的 SLAM 算法，LOAM(Lidar Odometry and Mapping)，则应用也相当广泛。本文从经典的 LOAM 出发，详细描述下激光 SLAM[1][2] 中的一些模块细节。

1. 问题描述

1.1. Scan 定义

　　针对旋转式机械雷达，Scan 为单个激光头旋转一周获得的点云，类似 VLP-16 旋转一周则是“几乎”同时获得了 16 个 Scan。针对棱镜旋转而激光头不旋转的雷达(Solid State LiDARs)，如大疆 Livox 系列，Scan 则可定义为一定时间下累积获得的点云。

1.2. Sweep 定义

　　Sweep 定义为静止的机器人平台上激光雷达能覆盖到所有空间的点云。
　　针对旋转式机械雷达，Sweep 即为旋转一周获得的由一个或多个 Scan 组成的点云。针对棱镜旋转而激光头不旋转的雷达，由于其属于非重复性扫描(Non-repetitive Scanning)结构，所以 Sweep 理论上为时间趋于无穷大时获得的点云，但是狭义上，可以认为一段较长时间下(相对于 Scan 时间)，获得的点云。
　　那么，如果给激光雷达加上一个马达呢？如图 1. 所示，[1] 中设计了一种 3D Lidar 装置，由一个只有一个激光头的 2D Lidar 和一个马达组成，激光扫描频率为 40Hz，马达转速为 180°/s。这种装置下，Scan 意义不变，Sweep 则为 1s 内该装置获得的点云(因为 1s 的时间内，该装置获得的点云可覆盖所有能覆盖的空间)。

1.2. 非重复性扫描激光雷达

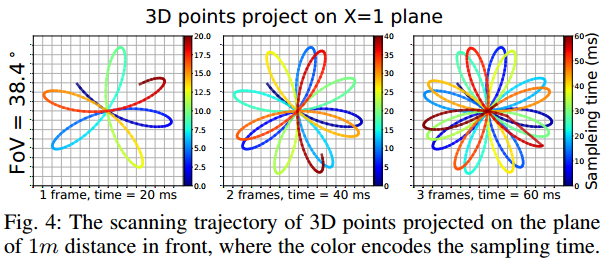　　其实，大疆的 Livox 非重复性扫描雷达相当于把这马达移到了内部的棱镜中，而且加上非对称，所以随着时间的累积，可获得相当稠密的点云。
　　Livox 这种非重复式扫描的激光雷达价格低廉，相对于传统的多线激光雷达有很多优点，但是有个致命的缺点：只能准确捕捉静态物体，无法准确捕捉动态物体；对应的，只能作 Mapping，很难作动态障碍物的估计。因为在一帧点云的扫描周期 \(T\) 内，如果目标速度为 \(v\)，那么 Livox 式雷达在扫描周期内都会扫到目标，目标的尺寸会被放大 \(Tv\)，而传统旋转的线束雷达真正扫到目标的时间为 \(t\ll T\)。当 \(T=0.1s\)，\(v=20m/s\) 时，尺寸放大为 2m，而一般小汽车车长也就几米。所以尺寸是估不准的，但是其它属性，如位置，速度，在目标加速度不是很大的情况下，可能还是有技巧可以估准的，具体就得看实验效果。另一种思路：直接对其进行物理建模，先假设已知目标速度，那么所有点即可恢复出目标的真实尺寸，然后可进一步估计速度，由此迭代至最优值。
　　由于本车的状态可以通过其它方式(如 IMU)获得，所以本车运动所引起的点云畸变(即 Motion Blur，基本所有雷达都会有这个问题，详见 2.3，4.1 章节)可以很容易得到补偿，所以对于静态目标，点云是能准确捕捉到其物理属性的。

1.3. 符号定义

　　本文首先基于图 1. 的装置进行 LOAM 算法的描述，一般的多线激光雷达或是 Livox 雷达则可以认为是图 1. 的特殊形式，算法过程很容易由此导出。
　　设第 \(k\) 次 Sweep 的点云为 \(\mathcal{P} _ k\)，Lidar 坐标系定义为此次 Sweep 初始扫描(也可定义为结束扫描)时刻 \(t_k\) 时， Lidar 位置下的坐标系 \(L\)，Sweep 由 \(S\) 个 Scan 组成，或由 \(I\) 个点组成，归纳为： \[\mathcal{P} _ k = \{\mathcal{P}_{(k,s)}\}_{s=1}^S = \{\mathit{X}_{(k,i)}^L\}_{i=1}^I \tag{1}\] 定义 \(\mathit{T} _ k^L(t)\) 为 Lidar 从时间 \(t_k\to t\) 的位姿变换；定义 \(\mathit{T} _ {k}^L(t_{(k,i)})\)(简写为 \(\mathit{T} _ {(k,i)}^L\)) 为 \(t_{(k,i)}\) 时刻接收到的点 \(\mathit{X} _ {(k,i)}\) 变换到坐标系 \(L\)，即 Sweep 初始时刻 Lidar 位置，的变换矩阵。
　　运动补偿问题： \[\{\mathit{T} _ {(k,i)}^L\} _ {i=1}^I \tag{2}\] 　　里程计问题： \[\mathit{T} _ K^L(t) \prod _ {k=1}^K\mathit{T} _ {k-1}^L(t _ {k}) \tag{3}\]

2. LOAM for 2D Lidar with Motor[1][2]

　　硬件装置如图 1. 所示，这里不再赘述，软件算法流程如图 3. 所示，\(\mathcal{\hat{P}} _ k=\{\mathcal{P} _ {(k,s)}\}\) 为累积的 Scan 点云，其都会注册到 \(L\) 坐标系，得到 \(\mathcal{P} _ k\)。Lidar Odometry 由 \(\mathcal{\hat{P}} _ k\) 注册到 \(\mathcal{P} _ {k-1}\) 生成高频低精度的位姿，并且生成运动补偿后的 Sweep 点云(这里也可以用其它的里程计实现，如 IMU 等)；Lidar Mapping 则由 \(\mathcal{P}_k\) 注册到世界坐标系 \(W\) 下的地图 \(\mathcal{P}_m\) 中，生成低频高精度的位姿和地图；Transform Integration 则插值出高精度高频的位姿。

2.1. Feature Extraction

　　这里提取的特征并没有描述子，更确切的说是找出有代表性的点。定义一种描述局部平面曲率的的变量： \[c = \frac{1}{\vert \mathcal{S}\vert\cdot \Vert\mathit{X} _ {(k,i)}^L\Vert} \left\Vert\sum _ {j\in\mathcal{S},j\ne i}\left(\mathit{X} _ {(k,i)}^L-\mathit{X} _ {(k,j)}^L\right)\right\Vert \tag{3}\] 其中 \(\mathcal{S}\) 为点 \(\mathit{X} _ {(k,i)}^L\) 相邻的同一 Scan 的点，其前后时序上各一半。根据 \(c\) 的值，由大到小选出 Edge Points 集，由小到大选出 Planar Points 集。最终选出的点需满足以下条件：

  1. 为了特征点的均匀分布，将空间进行栅格化，每个栅格最多容纳特定的点数；
  2. 被选择的点的周围点不会被选择；
  3. 对于 Planar Points 集中的点，如果其平面与雷达射线接近平行，那么则不予采用；
  4. 对于 Edge Points 集中的点，如果其处于被遮挡的区域边缘，那么也不予采用；

2.2. Feature Registration

　　如图 4. 所示，Lidar Odometry 模块的作用是将累积的 Scan 注册到上一时刻的 Sweep 中。设 \(\mathcal{\bar{P}} _ {k-1}\) 为点云 \(\mathcal{P} _ {k-1}\) 投影到 \(t _ {k}\) 的 Lidar 坐标系 \(L _ k\) 后的表示。\(\mathcal{\tilde{E}} _ k, \mathcal{\tilde{H}} _ k\) 为 \(\mathcal{\hat{P}} _ k\) 中提取的 Edge Points 与 Planar Points 集，并转换到了 \(L _ k\) 坐标系。

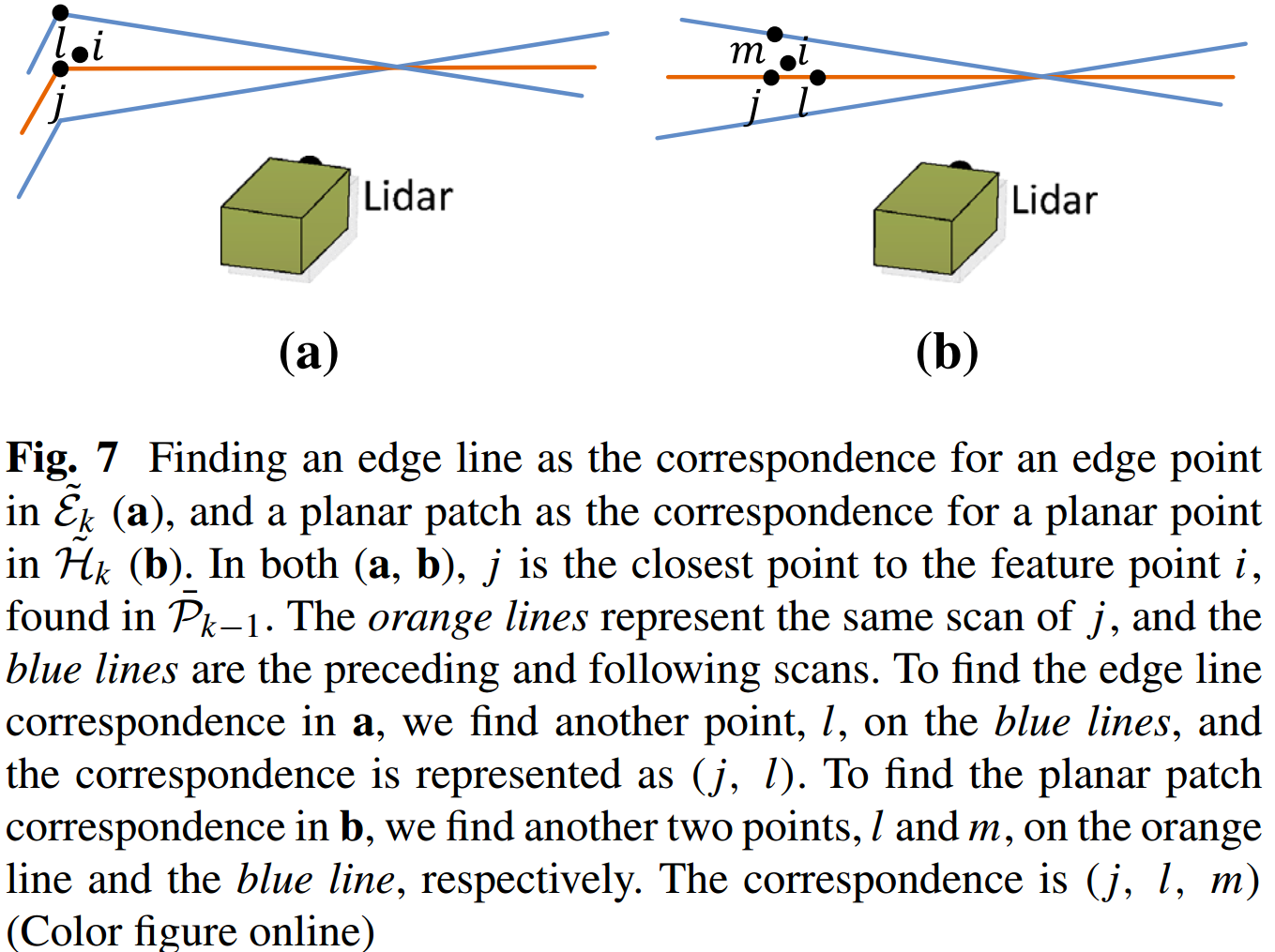
  1. Point to Edge
    对于点 \(i\in\mathcal{\tilde{E}} _ k\)，如图 4. 所示，找到其最近的点 \(j\in\mathcal{\bar{P}} _ {k-1}\)，并在点 \(j\) 前后相邻的两个 Scan 中找到与点 \(i\) 最近的点，记为 \(l\)（同一 Scan 不会打到同一 Edge 处）。通过式 (3) 进一步确认 \(j,l\) 是否满足 Edge Points 的条件，如果满足，那么直线 \((j,l)\) 则就是点 \(i\) 的对应直线，误差函数为： \[d _ {\mathcal{E}} = \frac{\left\vert \left(\mathit{\tilde{X}} _ {(k,i)}^L-\mathit{\bar{X}} _ {(k-1,j)}^L\right)\times\left(\mathit{\tilde{X}} _ {(k,i)}^L-\mathit{\bar{X}} _ {(k-1,l)}^L\right) \right\vert}{\left\vert\left(\mathit{\bar{X}} _ {(k-1,j)}^L-\mathit{\bar{X}} _ {(k-1,l)}^L\right)\right\vert} \tag{4}\]
  2. Point to Plane
    对于点 \(i\in\mathcal{\tilde{H}} _ k\)，如图 4. 所示，找到其最近的点 \(j\in\mathcal{\bar{P}} _ {k-1}\)，并在点 \(j\) 同一 Scan 中找到与点 \(i\) 第二近的点 \(l\)，在其前后相邻的两个 Scan 中找到与点 \(i\) 最近的点，记为 \(m\)。通过式 (3) 进一步确认 \(j,l,m\) 是否满足 Planar Points 的条件，如果满足，那么平面 \((j,l,m)\) 则就是点 \(i\) 的对应面，误差函数为： \[d _ {\mathcal{H}} = \frac{\left\vert \left(\mathit{\tilde{X}} _ {(k,i)}^L-\mathit{\bar{X}} _ {(k-1,j)}^L\right)^T\cdot\left(\left(\mathit{\bar{X}} _ {(k-1,j)}^L-\mathit{\bar{X}} _ {(k-1,l)}^L\right)\times\left(\mathit{\bar{X}} _ {(k-1,j)}^L-\mathit{\bar{X}} _ {(k-1,m)}^L\right)\right) \right\vert}{\left\vert\left(\mathit{\bar{X}} _ {(k-1,j)}^L-\mathit{\bar{X}} _ {(k-1,l)}^L\right)\times\left(\mathit{\bar{X}} _ {(k-1,j)}^L-\mathit{\bar{X}} _ {(k-1,m)}^L\right)\right\vert} \tag{5}\]

2.3. Motion Estimation

　　首先进行运动补偿，即求式(2)。记 \(\mathit{T} _ k^L(t) = [\mathit{R} _ k^L(t)\; \mathit{\tau} _ k^L(t)]\)。假设 \(t_k\to t\) 雷达为匀速运动，那么根据每个点的时间戳进行运动插值: \[\mathit{T} _ {(k,i)}^L = \begin{bmatrix} \mathit{R} _ {(k,i)}^L & \mathit{\tau} _ {(k,i)}^L \end{bmatrix} = \begin{bmatrix} e^{\hat{\omega}\theta s} & s\mathit{\tau} _ k^L(t) \end{bmatrix} = \begin{bmatrix} e^{\hat{\omega}\theta \frac{t _ {(k,i)}-t _ k}{t-t _ k}} & \frac{t _ {(k,i)}-t _ k}{t-t _ k}\mathit{\tau} _ k^L(t) \end{bmatrix} = \begin{bmatrix} \mathbf{I} + \hat{\omega} \mathrm{sin}\left(s\theta\right) + \hat{\omega}^2\left(1-\mathrm{cos}\left(s\theta\right)\right) & s\mathit{\tau} _ k^L(t) \end{bmatrix} \tag{6}\] 其中 \(\theta, \omega\) 分别是 \(\mathit{R} _ k^L(t)\) 的幅度与旋转角，\(\hat{\omega}\) 是 \(\omega\) 的 Skew Symmetric Matrix。
　　由此，对于特征点集，有如下关系： \[\begin{align} \mathit{\tilde{X}} _ {(k,i)}^L &= \mathit{T} _ {(k,i)}^L\mathit{X} _ {(k,i)} \\ \tag{7} \end{align}\] 带入式(4)(5)，可简化为以下非线性最小二乘优化函数： \[f(\mathit{T} _ {k}^L(t)) = \mathbf{d} \tag{8}\] 其中每一行表示一个特征点及对应的误差，用非线性优化使 \(\mathbf{d}\to \mathbf{0}\)： \[\mathit{T} _ {k}^L(t)\gets \mathit{T} _ {k}^L(t) - (\mathbf{J}^T\mathbf{J}+\lambda\mathrm{diag(\mathbf{J}^T\mathbf{J})})^{-1}\mathbf{J}^T\mathbf{d} \tag{9}\] 其中雅克比矩阵 \(\mathbf{J}=\frac{\partial f}{\partial \mathit{T} _ {k}^L(t)}\)；\(\lambda\) 由优化方法决定，如 LM，Gaussian-Newton 等。

2.4. Lidar Odometry

　　Lidar Odometry 模块生成 10Hz 的高频低精度雷达位姿(雷达 Scan 频率为 40Hz)，1Hz 的去畸变的点云帧，算法过程如图 5. 所示，优化时对每个特征点根据匹配距离作了权重处理。这里求取雷达位姿 \(\mathit{T} _ k^L(t)\) 是通过点云注册实现的，也完全可以采用其它里程计，如 IMU 等。

2.5. Lidar Mapping

　　Lidar Mapping 模块生成 1Hz 的低频高精度雷达位姿以及地图。式(3)后半部分表示的就是本模块要求的第 \(t_k\) 时刻在世界坐标系下的低频高精度位姿 \(\mathit{T} _ {k-1}^W(t _ k)\)。设累积到第 \(k-1\) 个 Sweep 的地图为 \(\mathcal{Q} _ {k-1}\)，第 \(k\) 次 Sweep 点云 \(\mathcal{\bar{P}} _ k\) 在世界坐标系下的表示为 \(\mathcal{\bar{Q}} _ k \)，将 \(\mathcal{\bar{Q}} _ k \) 注册到世界地图 \(\mathcal{Q} _ {k-1}\) 中，就求解出了位姿 \(\mathit{T} _ {k}^W(t _ {k+1})\)。
　　算法过程与 Lidar Odometry 类似，不同的是：

  1. 为了提升精度，特征点数量增加了好几倍(点云量也增多了，Sweep VS. Map)；
  2. 由于 Map 中无法区分相邻的 Scan，所以找 Map 中对应的 Edge 或 Planar 时，采用以下方法：找到该特征点在对应 Map 中最近的点集 \(\mathcal{S'}\)，计算该点集的协方差矩阵 \(\mathbf{M}\)，其特征值与特征向量为 \(\mathbf{V,E}\)。如果该点集分布属于 Edge Line，那么有一个显著较大的特征值，对应的特征向量代表该直线的方向；如果该点集分布属于 Planar Patch，那么有两个显著较大的特征值，最小特征值对应的特征向量表示了该平面的方向。由此找到 Point-to-Edge，Point-to-Plane 匹配。

　　建图时需要对 Map 进行采样，通过 Voxel-Grid Filter 保持栅格内点的密度，由此减少内存及运算量，Edge Points 的栅格应该要比 Planar Points 的小。
　　得到低频高精度雷达位姿后，结合 Lidar Odometry(式(3))，即可输出高频高精度(精度相对世界坐标系而言)的雷达位姿。

3. LOAM for Livox[3]

　　1.2 小节中已经阐述了 Livox 雷达的特性，这里整理如下：

  1. Small FoV
    包括 MEMS 这种 Solid State LiDARs，一般都有较小的视场角，不像旋转式机械雷达可达 360°；
  2. Irregular Scanning Pattern
    如图 2. 所示，雷达扫描出的 Pattern 是无规则的，这就导致有效特征提取的难度提升；
  3. Non-repetitive Scanning
    非重复性扫描，有利有弊；
  4. Motion Blur
    包括自身运动及目标运动所产生的点云畸变。自身运动所导致的点云畸变可以通过估计自身运动后，对点云进行运动补偿来矫正；而由于帧内周期均会扫描到目标，所以目标运动所产生的点云畸变影响较大，且基本无法消除。

3.1. Workflow

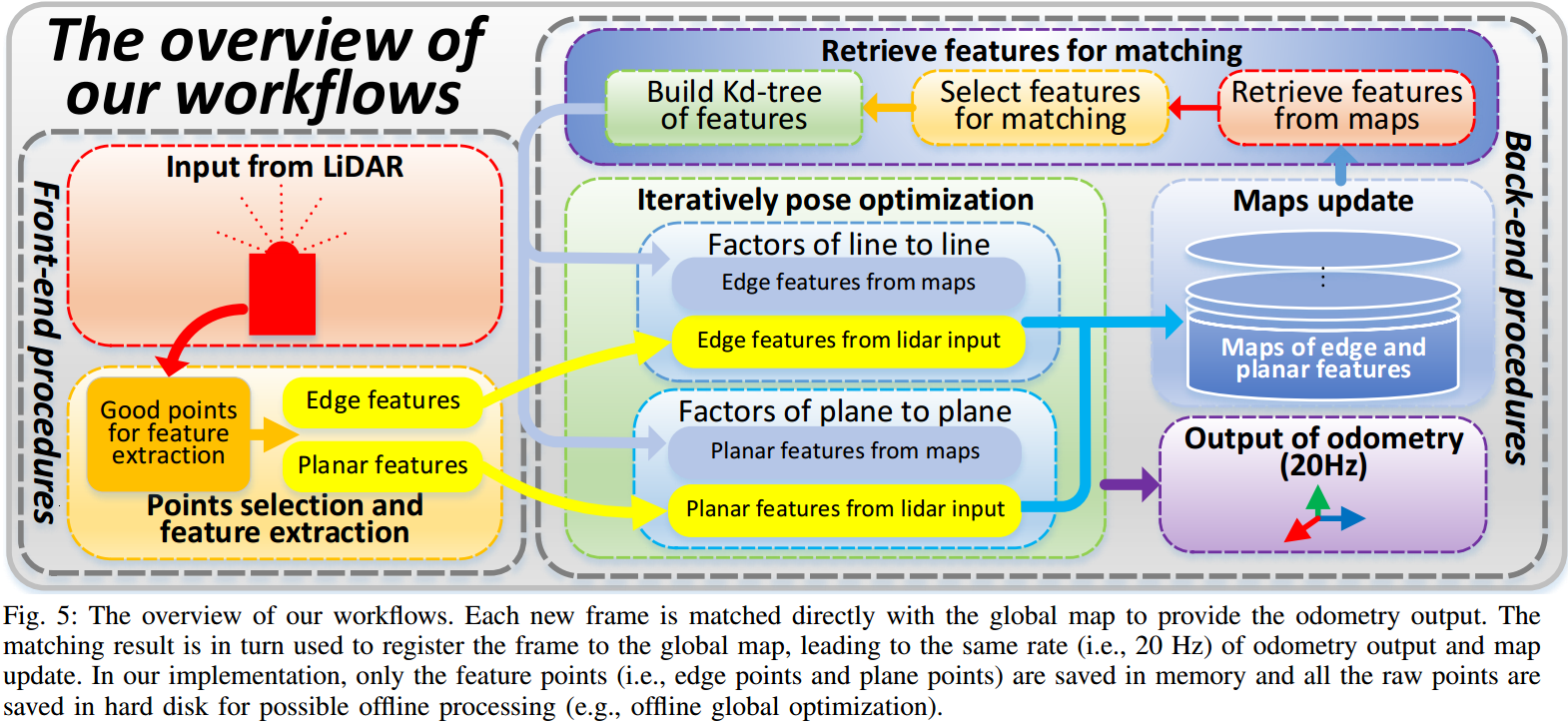　　Livox LOAM 可以认为是 LOAM 的简化版，直接从每帧的点云中提取出 Edge Points 和 Planar Points，经过线性插值的运动补偿后，在 Map 中找到对应的 Edge Line 与 Planar Patch，由此建立优化函数。相比于 LOAM，本文干掉了高频低精度的 Lidar Odometry(因为 Livox 没有前后 Scan 概念，很难做 Scan-to-Sweep 的点云注册)，直接出 20Hz 高频高精度的 Odometry 与 Map(计算平台强+软件多线程)。
　　此外本文针对雷达特性还作了更细致的工程改进，包括：

  1. 更严格的特征点选取
    去除视场边缘处的特征点；去除较大或较小反射强度的点；
  2. 改进的特征提取
    为了增多提取的特征点，将周围反射率变化较大的点也列入 Edge Points；
  3. Outlier Rejection
    在优化迭代时，先迭代两步，然后去除掉有较大误差的点，最后作进一步迭代；
  4. Dynamic Objects Filtering
    扣除掉动态障碍物的点云，这需要动态障碍物检测模块的支持；

4. LOAM for VLP-16[4]

4.1. Motion Blur

　　运动导致的点云畸变主要有两种：自身运动与目标运动。对于旋转式线束雷达来说，目标运动所导致的畸变基本可考虑不计(只有目标正好处于初始扫描与结束扫描的交界处时会有影响；Mapping 时则已扣掉动态障碍物，所以不影响)，这里主要讨论自身运动所导致的点云畸变影响。
　　每帧激光雷达数据(即一次 Sweep)都会标记到同一时间戳，假设标记到初始扫描的时刻。假设激光雷达旋转一周的扫描周期为 \(T\)，考虑一次 Sweep：\(t\in [0,T]\)。假设在扫描周期内自身为匀速运动，速度为 \(v\)，那么场景中点云的最大偏移畸变为 \(vT\)。考虑两次 Sweep: \(t _ 1,t _ 2\)，对应的速度为 \(v _ 1, v _ 2\)，那么两个时刻对同一物体的点云偏差量为 \(v _ 1T,v _ 2T\)。在世界坐标系下，该物体观测的点云最坏的不一致量可达到 \(|v _ 1T+v _ 2T|\)(自身运动有旋转的时候)，当然大多数情况可能是 \(|v _ 1T-v _ 2T|\)。

  1. 单帧情况
    当 \(T=0.1s,v=20m/s\) 时，畸变量为 2m，对于目标检测算法，虽然目标整体漂移了约 2m，不影响检测(尺寸未变)，但是直接导致观测的目标位置漂了约 2m！如果目标正好处于初始扫描和结束扫描的位置，那么目标的尺寸也会失真。
  2. 多帧情况
    这种情况指 Mapping 的过程。如果 \(t _ 1, t _ 2\) 时间跨度大，那么世界坐标系下同一物体的不一致性会相当高。如果是相邻 \(n\) 帧，假设自身加速度为 \(a = 5m/s^2\)，那么不一致量为 \(|v _ 1T-v _ 2T|=nTaT=0.05n\)，相邻帧可达 5cm ！

由此可见，不管是单帧任务还是多帧任务，点云的运动补偿不可不做。

4.2. Other

　　[4] 根据代码详细描述了 LOAM 应用到旋转式多线激光雷达的诸多细节，代码中采用了 IMU 里程计作为高频低精度的位姿估计。其它内容在以上章节中都有描述，这里就不再展开了。

5. Reference

[1] Zhang, Ji, and Sanjiv Singh. "LOAM: Lidar Odometry and Mapping in Real-time." Robotics: Science and Systems. Vol. 2. No. 9. 2014.
[2] Zhang, Ji, and Sanjiv Singh. "Low-drift and real-time lidar odometry and mapping." Autonomous Robots 41.2 (2017): 401-416.
[3] Lin, Jiarong, and Fu Zhang. "Loam_livox: A fast, robust, high-precision LiDAR odometry and mapping package for LiDARs of small FoV." arXiv preprint arXiv:1909.06700 (2019).
[4] https://zhuanlan.zhihu.com/p/57351961

----------------- END -----------------
坚持原创技术分享！