Model Compression - 'Quantization'

Posted on   |   Updated on | In | 本文总阅读量 次
Words count in article: 4.1k 字 | Reading time ≈ 18 分钟

　　量化(Quantization)是模型压缩主要技术之一。因为模型训练后的权重及特征图基本符合高斯分布(特征图可能是混合高斯分布)，所以将 32-bit 的张量量化到低比特后也能保持模型输出的准确度。如果只量化模型的权重，那么只是减少了模型的存储及传输大小；只有同时量化权重及特征图(Weight & Activation)，才能同时减少计算量。本文来详细描述下模型量化的细节。

1. Quantization Scheme

1.1. Fixed Point Approximation

　　设 Fixed Point 近似法中表示整数与小数的比特数分别为 \(\mathrm{IL,FL}\)，那么其可表达的浮点数范围为[1][2]：\([-2^{\mathrm{IL-1}}, 2 ^ {\mathrm{IL-1}}-2 ^ {-\mathrm{FL}}]\)。这种方法很明显，精度较差且表达的浮点数范围有限。更进一步，可以针对不同的张量，用不同的 \(\mathrm{IL,FL}\)，即 Dynamic Fixed Point 近似法[1]。综上，Fixed Point 近似法将一个浮点数表示为： \[(-1)^s\cdot 2^{-\mathrm{FL}}\sum _ {i=0}^{\mathrm{IL+FL-2}}2^i\cdot x _ i \tag{1}\] 其中 \(x_i\) 为第 \(i\) 比特位的值。
　　对于 Dynamic Fixed Point，首先保证整数部分不溢出，所以量化张量 \(X\) 时设计： \[\mathrm{IL}=\lceil\mathrm{lg} _ 2(\mathop{\max}\limits _ {S} X + 1)\rceil \tag{2}\] 剩下的比特位即为符号位与小数位。
　　用这种定点方式量化后，由式(1)可知，两数相乘可以转换为 bits shifts & add 操作，极大提升计算效率。
　　Fixed Point 近似法精度有限，尤其是当所要表示的值较大时，小数位 \(\mathrm{FL}\) 只能分到很小，所以精度必然有较大损失。

1.2. Range-Based Linear Approximation

　　不同于 Fixed Point 近似中小数位有一定限制(导致精度较差)，Range-Based Linear 近似法直接将浮点数通过一个高精度的 Scale 值映射到对应量化位数中，所以能保持非常高的精度。

1.2.1. Asymmetric Mode

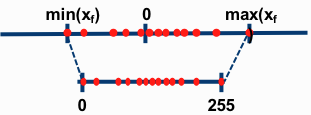　　如图 1. 所示，设浮点数为 \(r\)，那么 Asymmetric Linear Approximation 过程为[3]： \[q = round\left((r-r _ {min})\cdot\frac{2^n-1}{r _ {max}-r _ {min}}\right) = round(\frac{r}{S}-\frac{r _ {min}}{S}) \tag{3}\] 等价于[4]： \[r = S(q-Z) \tag{4}\] 其中 \(S\) 为映射的 Scale 参数，\(Z\) 表示零值被量化的值。 　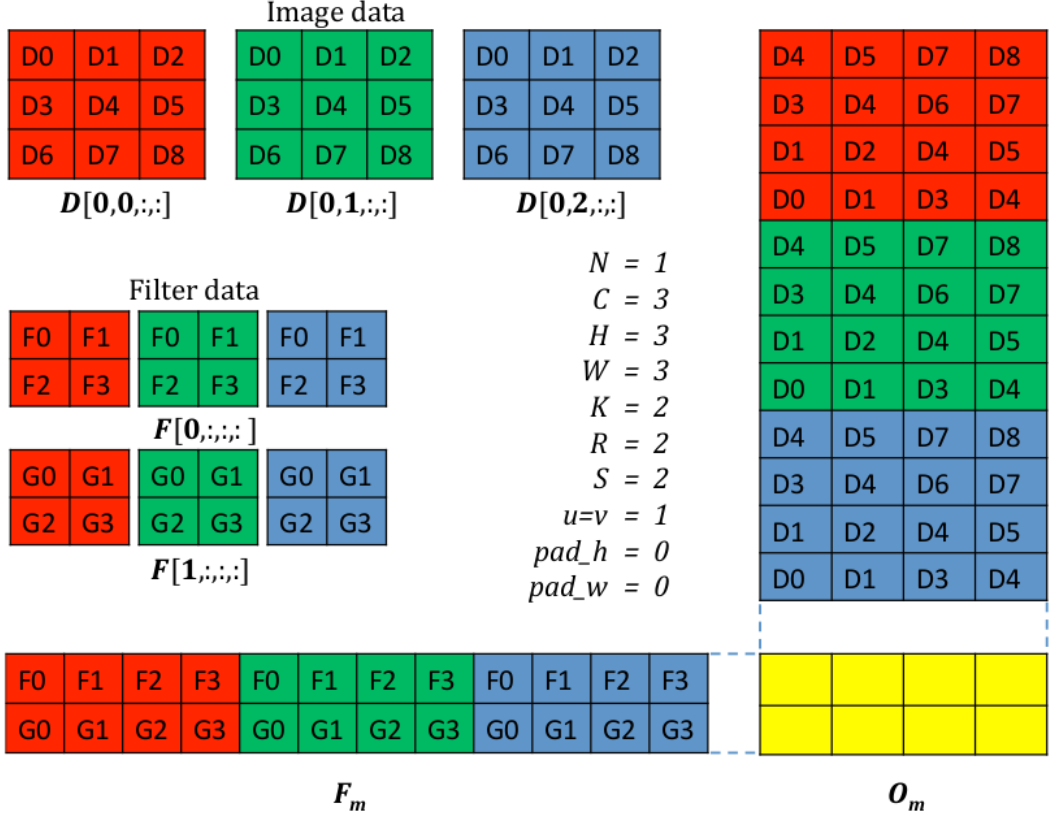　如图 2. 所示，卷积操作可转化为矩阵相乘运算，接下来我们来推导量化后的矩阵相乘运算。假设两个 \(N\times N\) 矩阵相乘：\(r _ 3=r _ 1\cdot r _ 2\)。令 \(r _ \alpha ^{(i,j)}\) 表示矩阵 \(r _ \alpha\) 第 \((i,j)\) 个元素，\(1\leq i,j\leq N\)。矩阵张量对应的量化参数为 \(S _ \alpha,Z _ \alpha\)，对应的量化后的元素表示为 \(q _ \alpha ^{(i,j)}\)： \[r _ \alpha ^{(i,j)} = S _ \alpha\left(q _ \alpha ^{(i,j)}-Z _ \alpha\right) \tag{5}\] bias 量化参数设为 \(S _ b=S _ 1S _ 2,Z _ b=0\)，那么卷积运算(矩阵相乘)可表示为： \[S _ 3\left(q _ 3 ^{(i,k)}-Z _ 3\right) = \sum _ {j=1} ^N S _ 1\left(q _ 1 ^{(i,j)}-Z _ 1\right)S _ 2\left(q _ 2 ^{(j,k)}-Z _ 2\right) + S _ b(q _ b^{(i)} - Z _ b)\tag{6}\] 等价于： \[\begin{align} q _ 3 ^{(i,k)} &= Z _ 3+M\left(\sum _ {j=1} ^N \left(q _ 1 ^{(i,j)}-Z _ 1\right)\left(q _ 2 ^{(j,k)}-Z _ 2\right)+ \frac{S _ b}{S _ 1S _ 2}q _ b^{(i)}\right) \\ &= Z _ 3+M\left(NZ _ 1Z _ 2- Z _ 1\sum _ {j=1}^Nq _ 2^{(j,k)}-Z _ 2\sum _ {j=1}^Nq _ 1^{(i,j)}+\sum _ {j=1}^N q _ 1^{(i,j)}q _ 2^{(j,k)}+ \frac{S _ b}{S _ 1S _ 2}q _ b^{(i)}\right) \\ &= Z _ 3+M\left(NZ _ 1Z _ 2- Z _ 1\sum _ {j=1}^Nq _ 2^{(j,k)}-Z _ 2\sum _ {j=1}^Nq _ 1^{(i,j)}+\sum _ {j=1}^N q _ 1^{(i,j)}q _ 2^{(j,k)}+ q _ b^{(i)}\right) \tag{7} \end{align}\] 其中 \(M=\frac{S _ 1S _ 2}{S _ 3}\) 可以离线计算，为上式唯一的浮点数。经验上可知 \(M\in(0,1)\)，进一步可将其表示为： \[M\approx 2^{-n}M _ 0 \tag{8}\] 假设 \(m\) 是能表示 \(M _ 0\) 的位数( int32 硬件下，\(m\) 可为 32)，那么有 \(2 ^ {n} M \leq 2 ^m -1\)，故： \[\left\{\begin{array}{l} n = \left\lfloor\mathrm{log} _ 2\frac{2 ^ m-1}{M}\right\rfloor \\ M _ 0 = \left\lfloor 2 ^ nM\right\rfloor \end{array}\tag{9}\right.\] 由此，乘以 \(M _ 0\) 可以用定点乘法实现，乘以 \(2 ^{-n}\) 可以用高效的位运算实现。式(7)中核心的计算为两个量化向量的乘加运算：\(\sum _ {j=1}^N q _ 1^{(i,j)}q _ 2^{(j,k)}\)，其可通过传统的特定位数的 BLAS 库完成。
　　具体的，令矩阵张量(卷积滤波器权重及特征图)量化为 8-bit，那么 8-bit 乘法需要用 32-bit 的累加器，即： \[\mathrm{int32 += uint8 * uint8} \tag{10}\] 所以式(7)中每一项累加时都是 32-bit 的，bias 也是量化为 32-bit 或是 rescale 到 32-bit，即 \(S _ b=S _ 1S _ 2,Z _ b=0\)。

1.2.2. Symmetric Mode

　　这种模式下最大最小值绝对值取相同值 \(R\) (该值可为任意值)，那么量化表示为： \[r = Sq \tag{11}\] Full Range 下 \(S = \frac{R}{(2^n-1)/2}\)(8-bit 则量化范围为 [-128,127]，Range 范围为 255)，Restricted Range 则 \(S = \frac{R}{2^{n-1}-1}\)(8-bit 量化范围为[-127,127]，Range 范围为 254)。Full Range 精度更高，PyTorch，ONNX 采用这种方式；TensorFlow，TensorRT，MKL-DNN 则采用 Restricted Range 量化方式。
　　由此式(7)简化为： \[q _ 3 ^{(i,k)} = M\left(\sum _ {j=1}^N q _ 1^{(i,j)}q _ 2^{(j,k)}+ q _ b^{(i)}\right) \tag{12}\] 实现更加简单。

2. Quantization Alogorithm

2.1. Post-Training Quantization

　　训练好的模型，可以直接对其权重进行量化，而对于特征的量化，则需要一个 Calibration 数据集来统计特征数值的分布，然后对其进行量化。
　　量化参数的搜索，可以根据量化后的模型好坏进行 Loss 构建：

  1. 任务级别损失函数：直接根据特定任务的指标来搜索及评价量化参数；
  2. 张量级别损失函数：设计量化后的张量与原始张量的分布相似度，或者说信息损失度，如 KL-divergence 等度量方法；

2.2. Quantization-Aware Training

　　将训练好的模型直接进行量化，可能会导致对应的任务准确度下降，尤其对表达能力有限的小模型而言，以下情况会导致量化后模型准确度下降：

  1. 权重张量中数值差异 100 倍以上，导致小数值的量化误差较大；
  2. 权重张量中有 outlier 值，导致其它值的量化误差较大；

而直接在训练的时候进行量化，可以保证完成模型训练也就得到了对应的高准确率的量化模型。 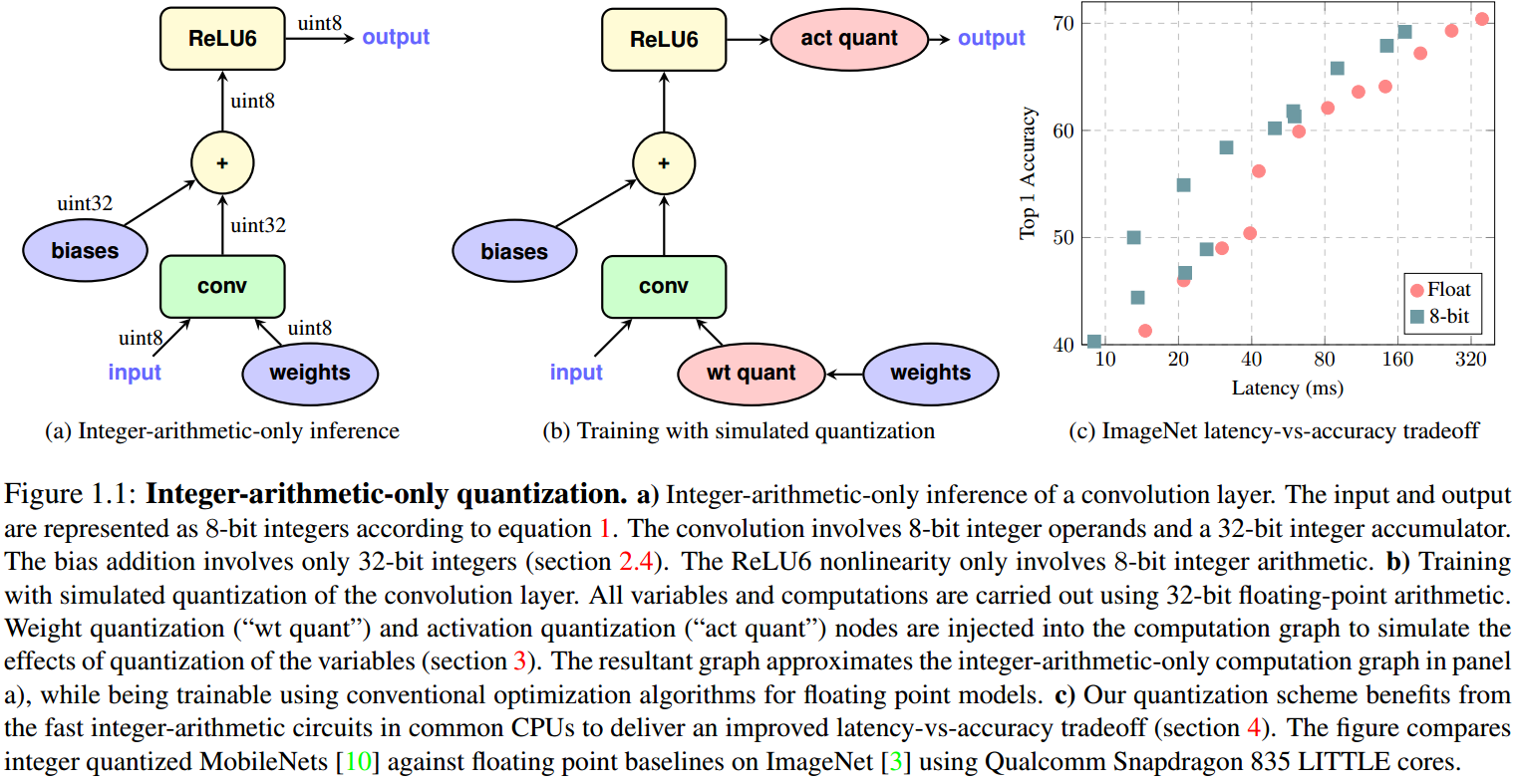　　如图 4. 所示，[4] 提出了一种 Quantization-Aware Training 的框架，权重和特征图均维护 float32 及 int8 数值，前向传播采用 int8 伪量化运算，反向传播更新权重的 float32 值，并作量化。 　　如图 5. 所示，[4] 基于 TensorFlow 实现了一种 Quantization-Aware Training 的算法，其步骤为：

  1. 建立一个浮点模型的 graph；
  2. 在 graph 中加入伪量化操作；
  3. 用伪量化的方式训练得到精度与浮点模型差不多的量化模型；
  4. 建立并优化量化的 Inference 模型 graph；
  5. 在量化引擎上作模型的 Inference；

2.2.1. Simulated Quantization

　　这里采用 Asymmetric Linear Approximation 量化策略。对于权重，卷积运算时，先做伪量化操作，并且如果有 batch-normalization，则将其合并入卷积核权重中；对于特征图(Activations)，前向传播时都先做伪量化操作。伪量化操作如下[4][5]： \[\begin{align} \mathrm{clamp}(r\;;a,b) &:= \mathrm{min}(\mathrm{max}(r,a),b) \\ s(a,b,n) &:= \frac{b-a}{2 ^n-1} \\ q(r\;;a,b,n) &:= \left\lfloor\frac{\mathrm{clamp}(r\;;a,b)-a}{s(a,b,n)}\right\rceil s(a,b,n)+a\\ \tag{13} \end{align}\] 其中 \([a,b]\) 是 被量化的浮点范围(可以是 \([r _ {min}, r _ {max}]\))，\(q(r\;;a,b,n)\) 即为浮点数 \(r\) 的伪量化表示，也是浮点数。

2.2.2. Learning Quantization Ranges

　　训练时，每次迭代，权重与特征图都要作伪量化处理，所以每次要确定量化参数。对于权重，因为其服从均值为零的高斯分布，所以 \([a,b]\) 直接设为其最大值与最小值即可；对于特征图，其数值与输入相关，所以策略为：刚开始训练的时候不对其作量化处理，之后用 EMA(Exponential Moving Averages) 对量化参数进行平滑，去除特征图输出突变的影响。

2.2.3. Batch Normalization Folding

　　作 Inference 或者说前向传播时，BN 可以合并入卷积核权重中，所以在量化前，先要将其合并，然后权重就仅限于卷积操作中。对于每个卷积 filter，其生成特征图以及 BN 过程如下： \[\begin{align} \hat{x} _ i &\gets wx _ i+b\\ \mu _ B &\gets \frac{1}{m}\sum _ {i=1}^m \hat{x} _ i\\ \sigma^2 _ B &\gets \frac{1}{m}\sum _ {i=1}^m(\hat{x} _ i-\mu _ B)^2\\ y _ i &\gets \gamma\frac{\hat{x} _ i-\mu _ B}{\sqrt{\sigma^2 _ B+\epsilon}} + \beta\\ \tag{14} \end{align}\] 由此可得： \[\begin{align} y _ i &\gets \gamma\frac{\hat{x} _ i-\mu _ B}{\sqrt{\sigma^2 _ B+\epsilon}} + \beta\\ &\gets \gamma\frac{wx _ i+b-\mu _ B}{\sqrt{\sigma^2 _ B+\epsilon}} + \beta\\ &\gets \frac{\gamma wx _ i}{\sqrt{\sigma^2 _ B+\epsilon}} +\frac{\gamma(b-\mu _ B)}{\sqrt{\sigma^2 _ B+\epsilon}}+ \beta\\ \tag{15} \end{align}\] 由此可知作 Inference 时，BN 参数 \(\mu _ B,\sigma^2 _ B,\gamma, \beta\) 可合并到卷积 Filter 参数中： \[\left\{\begin{array}{l} \hat{w} = \frac{\gamma w}{\sqrt{\sigma^2 _ B+\epsilon}}\\ \hat{b} = \frac{\gamma(b-\mu _ B)}{\sqrt{\sigma^2 _ B+\epsilon}}+ \beta\\ \end{array}\tag{16}\right.\]

2.3. Trained Quantization Thresholds

　　Post-Training Quantization 以及 Quantization-Aware Training 都是直接对张量的分析来搜索或近似求解量化参数的，Trained Quantization Thresholds 则在训练的时候同时训练得到量化参数。

2.3.1. PACT

　　PACT[13] 定义了激活函数输出的最大值，该最大值就是 Symmetric 量化中的激活层量化参数 Scale。具体的，改进 Relu： \[ y = \mathrm{PACT}(x) = 0.5(|x|-|x-\alpha|+\alpha)= \left\{\begin{array}{l} 0, \;\;x\in(-\infty,0)\\ x, \;\;x\in[0,\alpha]\\ \alpha, \;\;x\in[\alpha, +\infty) \end{array}\tag{17}\right.\] 对应的量化参数偏导为： \[\frac{\partial y _ q(x;\,\alpha)}{\partial \alpha}= \left\{\begin{array}{l} 0, \;\;x\in(-\infty, \alpha)\\ 1, \;\;x\in[\alpha,+\infty) \end{array}\tag{18}\right.\]

2.3.2. TQT

　　TQT(Trained Quantization Thresholds)[14]则提出了一种同时学习权重和激活函数的量化参数的方法。为了简化，其采用 Linear Symmetric Approximation，且 Scale 参数限定为 \(s=2 ^ {-f}\)，由式(8,9)可知，消除了定点乘法运算。前向传播与式(13)并无差异，对每个权重即激活层作 scale，round，saturate，de-quant 操作。反向传播则需要对量化值 \(q(x;s)\) 求导，量化值表示为： \[q(x;s)= \left\{\begin{array}{l} \left\lfloor\frac{x}{s}\right\rceil \cdot s, \;\; n\leq\left\lfloor\frac{x}{s}\right\rceil\leq p\\ n\cdot s, \;\;\;\;\left\lfloor\frac{x}{s}\right\rceil < n\\ p\cdot s, \;\;\;\;\left\lfloor\frac{x}{s}\right\rceil > p\\ \end{array}\tag{19}\right.\] 其中 \(n,p\) 分别为量化值域的最小最大值。定义 \(\frac{\partial \lfloor x\rceil}{\partial x} = 1\)，那么对 Scale 的偏导为： \[\nabla _ sq(x;s)= \left\{\begin{array}{l} \left\lfloor\frac{x}{s}\right\rceil - \frac{x}{s}, &\; n\leq\left\lfloor\frac{x}{s}\right\rceil\leq p\\ n, &\;\left\lfloor\frac{x}{s}\right\rceil < n\\ p, &\;\left\lfloor\frac{x}{s}\right\rceil > p\\ \end{array}\tag{20}\right.\] 为了稳定性，令 \(\nabla _ {(\mathrm{log} _ 2 t)} s = s\, \mathrm{In}(2)\)，则： \[\nabla _ {(\mathrm{log} _ 2t)}q(x;s)= s\,\mathrm{In}(2)\cdot \left\{\begin{array}{l} \left\lfloor\frac{x}{s}\right\rceil - \frac{x}{s}, &\; n\leq\left\lfloor\frac{x}{s}\right\rceil\leq p\\ n, &\;\left\lfloor\frac{x}{s}\right\rceil < n\\ p, &\;\left\lfloor\frac{x}{s}\right\rceil > p\\ \end{array}\tag{21}\right.\] 对应的，对输入 \(x\) 的偏导数为： \[\nabla _ xq(x;s)= \left\{\begin{array}{l} 1,&\; n\leq\left\lfloor\frac{x}{s}\right\rceil\leq p\\ 0, &\;otherwise\\ \end{array}\tag{22}\right.\]

　　由此可与网络权重一起训练得到量化参数。Graffitist[15]基于 TensorFlow 实现了上述算法；NNCF[16]基于 Pytorch 实现了类似算法。

3. Quantized Framework

　　不管是 Post-Training Quantization 还是 Quantization-Aware Training，算法端都还是用伪量化操作实现的，部署时就必须用 INT8 引擎。据我所知目前 INT8 引擎有：

  1. DSP/加速芯片平台
    目测没有开源的，大家自个玩自个的；
  2. CPU 平台
    Google 的 TensorFlow Lite[6]，Facebook 的 QNNPACK[8]，Tencent 的 NCNN[9]。
  3. GPU 平台
    NVIDIA 的 TensorRT[10]，TVM[11]。

而伪量化框架则在深度学习框架(caffe，pytorch，tensorflow)中开源的较多，如基于 pytorch 的 distiller[3]，NNCF[16]。
　　对于 ARM 平台，INT8 引擎会通过 NEON 指令集加速；对于 x86 平台，INT8 引擎会通过 SSE 加速；对于 NVIDIA GPU 平台，则通过 dp4a[12] 矩阵运算库加速。dp4a 实现了基础的 INT8 矩阵相乘操作，目前 cuDNN，cuBLAS，TensorRT 均采用该指令集。下面对 INT8 引擎作简要阐述。

3.1. Ristretto[1]

　　Ristretto 是一种基于 (Dynamix) Fixed Point Approximation, Post-Training Quantization 的量化框架，其精度有限，量化的 Inference 引擎可用 bits shifts & add 操作实现，比较适合应用于 DSP 等嵌入式平台。

3.2. TensorFlow Lite[6]/QNNPACK[8]/NCNN[9]

　　TensorFlow Lite 是 Google 基于 TensorFlow 开发的针对移动嵌入式 CPU 平台的模型(量化)加速框架，其实现在 2.2 小节中已有详细的描述，有较高精度，[4] 实现了 Quantization-Aware Training。其中 INT8 矩阵运算采用了 gemmlowp[7]。
　　移动端的 CPU 的量化计算引擎开源的也比较多，如 Facebook 的 QNNPACK[8]，腾讯的 ncnn-int8[9]。

3.3. TensorRT[10]

　　TensorRT 是 NVIDIA 基于 GPU 平台的模型(量化)加速框架，其基于 Symmetric Linear Approximation 量化策略，并且只支持 Post-Training Quantization，其内部可能直接调用 dp4a，也可能调用 cuDNN 或 cuBLAS。TVM[11] 调用 dp4a 实现了基于 python 的 INT8 引擎，对于部署来讲没有 TensorRT 高效。
　　对于特征图的量化参数 \(S\) 的搜索，其使用张量级别的损失函数，最小化量化前后特征图值分布差异性的方式，KL-divergency，即两个分布的相对熵。假设连个分布 \(P,Q\)，那么两者的相对熵为： \[E(P,Q) = \sum _ i P(i)\cdot\mathrm{log}\left(\frac{P(i)}{Q(i)}\right) \tag{23}\] 熵越大，表示两个分布差异性越大，即量化后信息损失越大。这里也可以采用其它能描述两个分布差异性的方式，如 EMD。整个量化参数搜索过程为：

  1. 准备训练好的 FP32 模型，以及一个作校正(Calibration)的数据集；
  2. 用 FP32 模型跑数据集，统计每个特征图的值分布；
  3. 对不同的量化参数，根据式(17)计算量化前后的相对熵；选择最优的量化参数；
  4. 根据最优的量化参数量化特征图得到量化模型(权重值分布比较集中，所以可以直接用最大值作为量化参数，具体还得看 TensorRT 怎么做的)；
  5. 保存量化参数为 Calibration Table，载入该值即可启动 INT8 引擎作量化 Inference；

4. Reference

[1] Gysel, Philipp. "Ristretto: Hardware-oriented approximation of convolutional neural networks." arXiv preprint arXiv:1605.06402 (2016).
[2] Gupta, Suyog, et al. "Deep learning with limited numerical precision." International Conference on Machine Learning. 2015.
[3] https://nervanasystems.github.io/distiller/index.html
[4] Jacob, Benoit, et al. "Quantization and training of neural networks for efficient integer-arithmetic-only inference." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018.
[5] Krishnamoorthi, Raghuraman. "Quantizing deep convolutional networks for efficient inference: A whitepaper." arXiv preprint arXiv:1806.08342 (2018).
[6] https://www.tensorflow.org/mobile/tflite
[7] https://github.com/google/gemmlowp
[8] https://github.com/pytorch/QNNPACK
[9] https://github.com/Tencent/ncnn/pull/487
[10] Migacz, Szymon. "8-bit inference with tensorrt." GPU technology conference. Vol. 2. No. 4. 2017.
[11] https://tvm.apache.org/2019/04/29/opt-cuda-quantized
[12] https://devblogs.nvidia.com/mixed-precision-programming-cuda-8/
[13] Choi, Jungwook, et al. "Pact: Parameterized clipping activation for quantized neural networks." arXiv preprint arXiv:1805.06085 (2018).
[14] Jain, Sambhav R., et al. "Trained quantization thresholds for accurate and efficient neural network inference on fixed-point hardware." arXiv preprint arXiv:1903.08066 (2019).
[15] https://github.com/Xilinx/graffitist
[16] Kozlov, Alexander, et al. "Neural Network Compression Framework for fast model inference." arXiv preprint arXiv:2002.08679 (2020).

----------------- END -----------------
坚持原创技术分享！