之前介绍了 JSNet, JSIS3D，PointGroup 等 Instance 分割方法，为了点云聚类成 Instance，网络输出基本分为每个点距离目标中心的坐标残差以及每个点的 Embedding 特征两种。对于目标中心的坐标残差，之后可以直接在几何空间内作基于距离的聚类；对于每个点的 Embedding 特征，由于训练时要求同一个 Instance 内的 Embedding 相近，不同的距离要远，所以也是通过高维空间的距离计算来作聚类。
本文[1]大致也是这个思路，此外还预测了每个 voxel 的 Occupancy Regression，表示对应 Instance 包含的 Voxel 数目。最后采用基于图的聚类方法得到 Instance。
1. Framework
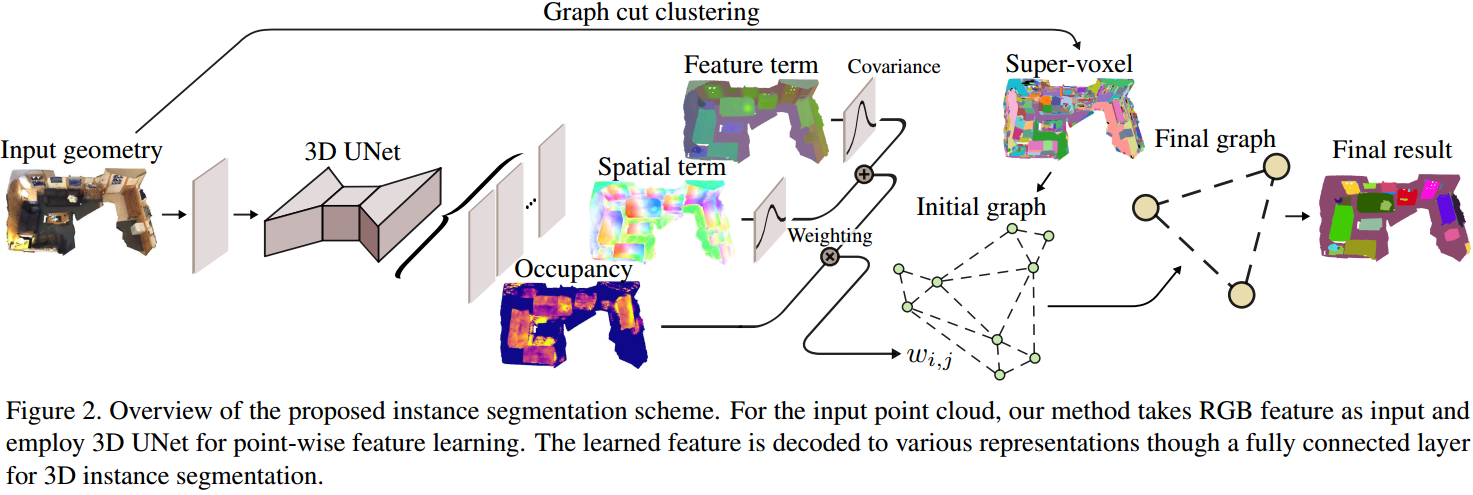如图 1. 所示，网络输入为 RGBD 点云数据，通过 3D UNet Backbone 网络，输出基于 Voxel 的三种预测结果：
- Semantic Segmentation
语义分割结果 \(\mathbf{c} _ i\)。 - Spatial Embedding and Feature Embedding
基于坐标系的残差预测 \(\mathbf{d} _ i\)，和基于特征空间的 Embedding 预测 \(\mathbf{s} _ i\)，以及对应的方差 \(\mathbf{b} _ i=(\sigma _ d ^ i,\sigma _ s ^ i)\)。 - Occupancy Regression
预测该 Voxel 对应 Instance 所含有的 Voxel 数量 \(\mathbf{o} _ i\)。
Loss 项目构成为： \[\mathcal{L} _ {joint} = \mathcal{L} _ {c} + \mathcal{L} _ {e} + \mathcal{L} _ {o} \tag{1}\]
1.1. Spatial and Feature Embedding
Embedding 的 Loss 项构成为： \[\mathcal{L} _ e = \mathcal{L} _ {sp} + \mathcal{L} _ {se} + \mathcal{L} _ {cov} \tag{2}\] 其中 Spatial Embedding 目的是回归每个 voxel 与目标中心点的残差： \[\mathcal{sp}=\frac{1}{C}\sum _ {c=1} ^ C\frac{1}{N _ c}\sum _ {i=1} ^ {N _ c}\Vert \mathbf{d} _ i+\mu _ i-\frac{1}{N _ c}\sum _ {i=1} ^ {N _ c}\mu _ i\Vert \tag{3}\] \(C\) 表示 Instance 数量，\(N _ c\) 表示第 \(c\) 个 Instance 包含的 Voxel 数量，\(\mu _ i\) 表示第 \(i\) 个 voxel 的坐标。
Feature Embedding 目的是相同 Instance 的 voxel 预测相似的特征，不同的则预测不同的特征，通过 Metric Learning 实现： \[\begin{align}
\mathcal{L} _ {se} &=\mathcal{L} _ {var}+\mathcal{L} _ {dist} +\mathcal{L} _ {reg}\\
&= \frac{1}{C}\sum _ {c=1} ^ C\frac{1}{N _ c}\sum _ {i=1} ^ {N _ c}\left[\Vert\mathbf{u} _ c-\mathbf{s} _ i\Vert -\delta _ v\right] _ + ^ 2 + \frac{1}{C(C-1)}\mathop{\sum _ {i=1} ^ C\sum _ {j=1} ^ C} \limits _ {i\neq j}\left[2\delta _ d-\Vert\mathbf{u} _ i-\mathbf{u} _ j\Vert \right] _ + ^ 2 + \frac{1}{C}\sum _ {c=1} ^ C\Vert\mathbf{u} _ c\Vert
\tag{4}
\end{align}\] 其中 \(\mathbf{u} _ c=\frac{1}{N _ c}\sum _ {i=1} ^ {N _ c} \mathbf{s} _ i\) 表示第 \(c\) 个 Instance 的平均 Embedding 特征。以上和 JSNet, JSIS3D 基本一致。
此外本文还预测了 Covariance 项。设预测的 Feature 和 Spatio Covariance 为 \(\mathbf{b} _ i=(\sigma _ s ^ i, \sigma _ d ^ i)\)，对 Instance 内的 voxel covariance 融合可得到该 Instance 的 Covariance \((\sigma _ s ^ c,\sigma _ d ^ c)\) (这里需要注意的是，Inference 的时候，即作基于图分割算法的聚类时候，见1,3，是只需要作 super-voxel 内的 Covariance 融合；而训练的时候，是由 Instance 标签的，所以能通过 Instance 的 Covariance 融合，以重构 \(p _ i\))。由此可得到第 \(i\) 个 voxel 属于第 \(c\) 个 Instance 的概率： \[p _ i = \mathrm{exp}\left(-\left(\frac{\Vert\mathbf{s} _ i-\mathbf{u} _ c\Vert}{\sigma _ s ^ c}\right)^2-\left(\frac{\Vert \mu _ i+\mathbf{d} _ i-\mathbf{e} _ c\Vert}{\sigma _ d ^ c}\right)^2\right)\tag{5}\] 其中 \(\mathbf{e} _ c=\frac{1}{N _ c}\sum _ {k=1} ^ {N _ c}(\mu _ k+\mathbf{d} _ k)\) 表示预测的目标中心点。当 \(p _ i\) 大于 0.5 时，就表示该 voxel 属于该 Instance，所以用 binary cross-entropy loss： \[\mathcal{L} _ {cov} = -\frac{1}{C}\sum _ {c=1}^C\frac{1}{N}\sum _ {i=1} ^ N[y _ i\mathrm{log}(p _ i)+(1-y _ i)\mathrm{log}(1-p _ i)]\tag{6}\] 其中 \(y _ i\) 为标签，1 表示该 voxel 属于该 Instance，0 表示不属于。
1.2. Occupancy Regression
每个 Voxel 预测其对应的 Instance 包含的 Voxel 数目 \(o _ i\)，为了预测的鲁棒性，设计为回归其 log 值： \[\mathcal{L} _ o = \frac{1}{C}\sum _ {c=1} ^ C\frac{1}{N _ c}\sum _ {i=1} ^ {N _ c}\Vert o _ i-\mathrm{log}(N _ c)\Vert \tag{7}\] 其中 \(N _ c\) 是第 \(c\) 个 Instance 包含的 Voxel 数量。
1.3. Instance Clustering
基于每个 Voxel 的预测：Semantic Label，Spatial and Feature Embedding，Occupancy Regression，本文采用自底向上的图分割算法。
设 \(\Omega _ i\) 为上层 super-voxel \(v _ i\) 包含的 Voxel 数量。\(v _ i\) 对应的 Spatial Embedding，Feature Embedding，Occupancy Regression 为： \[\left\{\begin{array}{l}
\mathbf{D} _ i =\frac{1}{\vert\Omega _ i\vert}\sum _ {k\in\Omega _ i}(\mathbf{d} _ k+\mu _ k)\\
\mathbf{S} _ i =\frac{1}{\vert\Omega _ i\vert}\sum _ {k\in\Omega _ i}(\mathbf{s} _ k)\\
\mathbf{O} _ i =\frac{1}{\vert\Omega _ i\vert}\sum _ {k\in\Omega _ i}(\mathrm{exp}(\mathbf{o} _ k))\\
\end{array}\tag{8}\right.\] 为了指导聚类过程，定义(文章中应该是写反了)： \[r _ i=\frac{\vert\Omega _ i\vert}{O _ i} \tag{9}\] \(r _ i>1\) 表示该 Instance 聚类的 Voxel 太多了，即欠分割；反之即为过分割。
图分割算法定义图 \(G=(V,E,W)\)，其中 \(v _ i\in V\) 表示 super-voxel，\(e _ {i,j}\) 表示 \((v _ i, v _ j)\in E\) 通过全概率权重 \(w _ {i,j}\in W\) 连接。\(w _ {i,j}\) 可定义为两个 super-voxel 的相似度： \[w _ {i,j}=\frac{\mathrm{exp}\left(-\left(\frac{\Vert\mathbf{S} _ i-\mathbf{S} _ j\Vert}{\sigma _ s}\right) ^ 2-\left(\frac{\Vert \mathbf{D} _ i-\mathbf{D} _ j\Vert}{\sigma _ d}\right) ^ 2\right)}{\mathrm{max}(x,0.5)} \tag{10}\] 自底向上迭代聚类通过 \(w _ {i,j} > T _ 0\) 实现，\(T _ 0\) 设定为 0.5，最后保留 \(0.3 < r<2\) 的 Instance，以减少 FP。
2. Reference
[1] Han, Lei , et al. "OccuSeg: Occupancy-aware 3D Instance Segmentation." (2020).
