自动驾驶的障碍物状态估计功能模块中，包含 perception/Detection，tracking，prediction 三个环节。传统的做法这三个环节是分步进行的，Detection 出目标框检测结果；Tracking 则作前后帧目标的数据关联然后用卡尔曼平滑并估计目标状态；Prediction 预测目标未来的运动轨迹。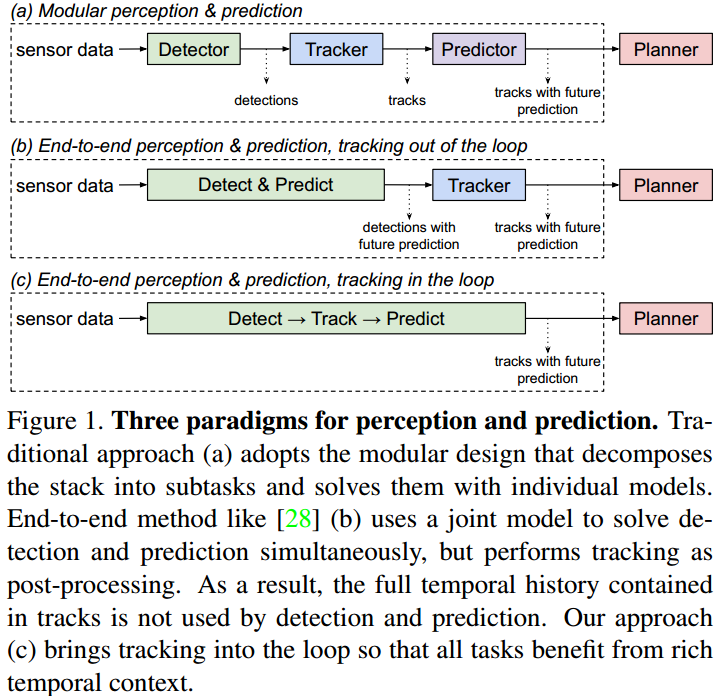 
如图 1. 所示，(a) 代表传统的做法，每个步骤都是独立优化并出结果，这种方式将功能模块解耦，容易找到具体问题的位置，但是会降低算法找到最优解的概率；(b) 则将 Detection 与 Prediction 用同一个网络预测，然后用 Tracking 来平滑估计整个运动轨迹(代表方法是 Fast and Furious)，这种方法下 Tracking 中丰富的时序及空域特征信息没有作用于 Detection 和 Prediction；本文提出的 PnP[1]方法则将三个环节作深度的特征再利用，即整个功能模块是 End-to-End 可训练的，更容易得到目标状态及预测的全局最优解，更容易处理遮挡等问题。
1. Framework
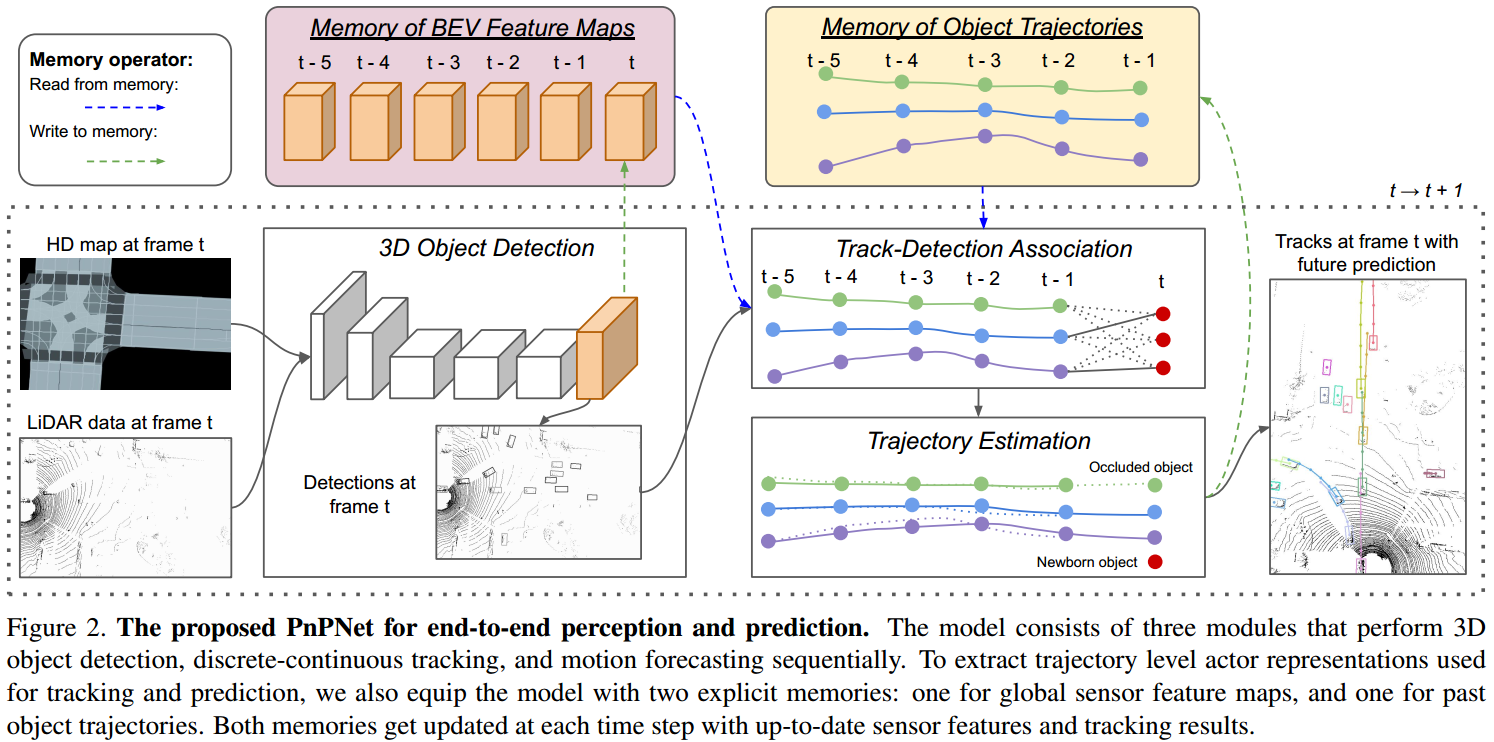如图 2. 所示，PnP 网络包含 Detection、Tracking，Motion Forecasting 三个模块。网络输入为点云及 HD Map。检测模块包含一个任意的 3D 目标检测网络，以及一个存储历史 BEV 特征图的 Memory；Tracking 跟踪模块包含一个存储目标历史轨迹的 Memory，首先作 Track-Detection 的数据关联，然后优化目标历史轨迹并更新存储；Motion Forecasting 模块则根据历史轨迹作目标的运动预测。
2. Object Detection
网络的输入为序列点云(本文采用 0.5s)及 HD Map，分别将点云在俯视图下体素化后在特征通道维度进行串联得到 \(\mathbf{x} ^ t\)，然后输入 Backbone 网络得到俯视图下特征图： \[\mathcal{F} ^ t _ {bev}(\mathbf{x} ^ t) = \mathrm{CNN} _ {bev}(\mathbf{x} ^ t) \tag{1}\] 最后加入 3D 目标检测头，得到 3D 目标框属性 \((u _ i ^ t, v _ i ^ t,w _ i,l _ i,\theta _ i ^ t)\) 的预测： \[\mathcal{D} ^ t=\mathrm{CNN} _ {det}(\mathcal{F} ^ t _ {bev})\tag{2}\]
3. Discrete-Continuous Tracking
Tracking 模块包括离散的数据关联问题，以及连续的目标运动轨迹(状态)估计问题。目标运动轨迹的优化估计对之后的目标运动预测非常重要。
3.1. Trajectory Level Object Representation
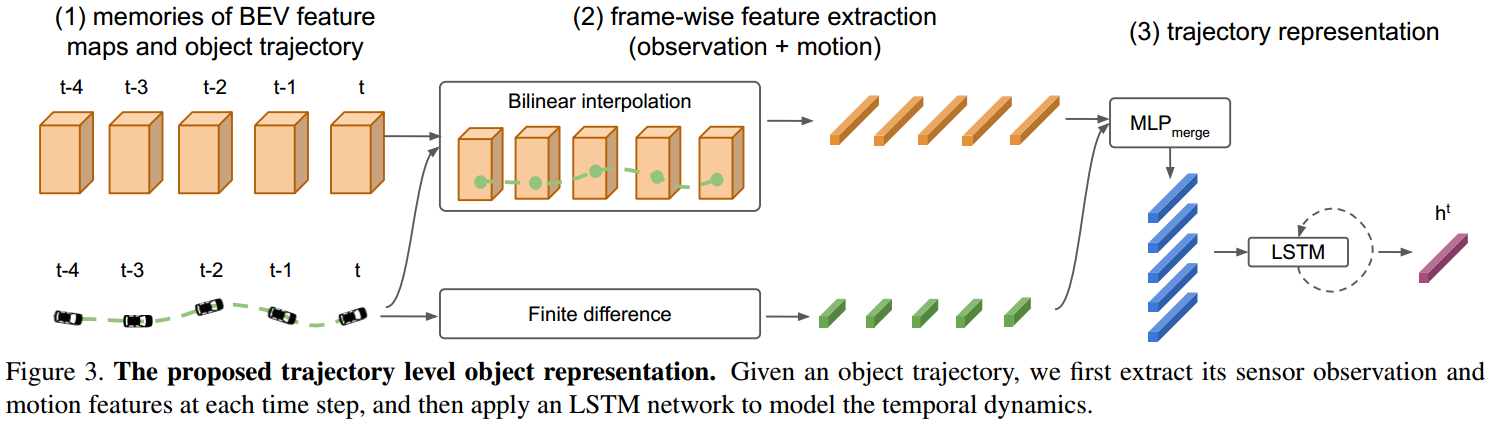Tracking 需要优化历史轨迹，Prediction 需要预测未来轨迹，所以轨迹级别的目标特征提取及表达非常重要。本文采用 LSTM 网络来表征。如图 3. 所示，对于轨迹 \(\mathcal{P} _ i ^ t=\mathcal{D} _ i ^ {t _ 0...t}\)，首先提取每个时刻目标的感知特征： \[f _ i^{bev,t} = \mathrm{BilinearInterp}(\mathcal{F} _ {bev} ^ t,(u _ i ^ t, v _ i ^ t)) \tag{3}\] 然后提取目标运动特征： \[f _ i ^ {velocity,t}=(\dot{x} _ i ^ t,\dot{x} _ {ego} ^ t, \dot{\theta} _ {ego} ^ t)\tag{4}\] 其中 \(\dot{x} _ i,\dot{x} _ {ego}\) 分别是第 \(i\) 个目标及本车的二维速度，通过位置差计算得到，对于新目标，将其设定为 0。由此得到第 \(i\) 个目标的特征： \[f(\mathcal{D} _ i ^ t)=\mathrm{MLP} _ {merge}\left(f _ i^{bev,t},f _ i ^ {velocity,t}\right)\tag{5}\] 最后通过 LSTM 网络来提取轨迹级别目标特征： \[h(\mathcal{P} _ i ^ t)=\mathrm{LSTM}(f(\mathcal{D} _ i ^ {t _ 0...t}))\tag{6}\]
3.2. Data Association
当前时刻检测的目标数量为 \(N _ t\)，上一时刻目标轨迹数量为 \(M _ {t-1}\)，将二者关联匹配就是数据关联问题。这在有新目标出现以及目标出现遮挡的时候变得较为困难。类似传统方法，这里设计检测与跟踪轨迹的相似性矩阵 \(C\in\mathbb{R} ^ {N _ t\times (M _ {t-1}+N _ t)}\)(跟踪轨迹加入\(N _ t\)个目标是为了处理新出现目标的情况)： \[C _ {i,j}=\left\{\begin{array}{l}
\mathrm{MLP} _ {pair}\left(f(\mathcal{D} _ i ^ t),h(\mathcal{P} _ j ^ {t-1})\right) &\;\; \mathrm{if}\; 1\leq j\leq M _ {t-1},\\
\mathrm{MLP} _ {unary}\left(f(\mathcal{D} _ i ^ t)\right) &\;\; \mathrm{if}\; j= M _ {t-1} + i,\\
-\mathrm{inf} &\;\; \mathrm{otherwise}
\end{array}\tag{7}\right.\] 其中 \(\mathrm{MLP} _ {pair}\) 计算检测与跟踪轨迹的相似性分数，\(\mathrm{MLP} _ {unary}\) 计算目标是新出现的概率。有了该相似性矩阵，即可通过匈牙利算法求解最佳匹配对。
对于被遮挡的物体，跟踪轨迹在当前帧容易出现没有检测的情况，本文引入单目标跟踪的思想作跟踪搜索。设未匹配的跟踪轨迹为 \(\mathcal{P} _ j ^ {t-1}\)，那么根据上一帧该轨迹目标的位置 \(u _ j ^ {t-1}, v _ j ^ {t-1}\)，进行运动补偿后为 \(\tilde{u} _ j ^ {t}, \tilde{v} _ j ^ {t}\)，在其邻域 \(\Omega _ j\) 内寻找最优的检测(跟踪)结果 \(\tilde{\mathcal{D}} _ k ^ t\)： \[k = \mathop{\arg\max}\limits _ {i\in\Omega _ j} \mathrm{MLP} _ {pair}\left(f(\tilde{\mathcal{D}} _ i ^ t),h(\mathcal{P} _ j ^ {t-1})\right)\tag{8}\] 其中 \(\Omega _ j\) 设计为目标的最大假设速度，如 \(110 km/h\)。
最终可得到 \(N _ t+ K _ t\) 个目标轨迹，其中 \(K _ t\) 为未匹配的目标轨迹而通过单目标跟踪方法召回的轨迹数量。
3.3. Trajectory Estimation
当前帧的观测加入到目标轨迹后，可进一步对目标轨迹作优化以减少 FP 以及提高轨迹定位精度。网络预测轨迹的置信度以及最近 \(T _ 0\) 时间内目标位置的残差： \[\mathrm{score} _ i,\Delta u _ i ^ {t-T _ 0+1:t},\Delta v _ i ^ {t- T _ 0+1:t}=\mathrm{MLP} _ {refine}(h(\mathcal{P} _ i^t))\tag{9}\] 其中 \(T _ 0\) 小于轨迹的总时间。最后用 NMS 去掉重叠的目标轨迹以消除 FP 与重叠项。
4. Motion Forecasting
根据优化后的目标轨迹，通过网络预测目标的未来轨迹： \[\Delta u _ i^{t:t+\Delta T}, \Delta v _ i ^ {t:t+\Delta T}=\mathrm{MLP} _ {predict}(h(\mathcal{P} _ i^t))\tag{10}\]
5. End-to-End Learning
整个网络多任务联合训练的 Loss 为： \[\begin{align} \mathcal{L} &= \mathcal{L} _ {detect} + \mathcal{L} _ {track} + \mathcal{L} _ {predict}\\ &= \mathcal{L} _ {detect} + \mathcal{L} _ {score} ^ {affinity} + \mathcal{L} _ {score} ^ {sot} + \mathcal{L} _ {socre} ^ {refine} + \mathcal{L} _ {reg} ^ {refine} + \mathcal{L} _ {predict} \end{align}\tag{11}\] 其中 \(\mathcal{L} _ {score}\) 为 \(max-margin \;loss\): \[\mathcal{L} _ {score} = \frac{1}{N _ {i,j}}\sum _ {i\in pos,j\in neg} \mathrm{max}(0,m-(a _ i-a _ j))\tag{12}\] 对于 \(\mathcal{L} _ {score} ^ {affinity}\) 和 \(\mathcal{L} _ {score} ^ {sot}\)，计算正样本与所有负样本的 Loss；对于 \(\mathcal{L} _ {score} ^ {refine}\)，与真值框 IoU 较高的，则 score 较高，这样作 NMS 时可以该 score 为准则。
6. Reference
[1] Liang, Ming, et al. "PnPNet: End-to-End Perception and Prediction with Tracking in the Loop." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020.
