之前一直提到，以 Semantic Segmentation 为基础作目标检测，可以有较高的召回率，而在最终出目标框或目标 Polygon 之前，还需要作 Instance Segmentation。本文[1] 介绍一种 Instance Segmentation 方法。
1. Framework
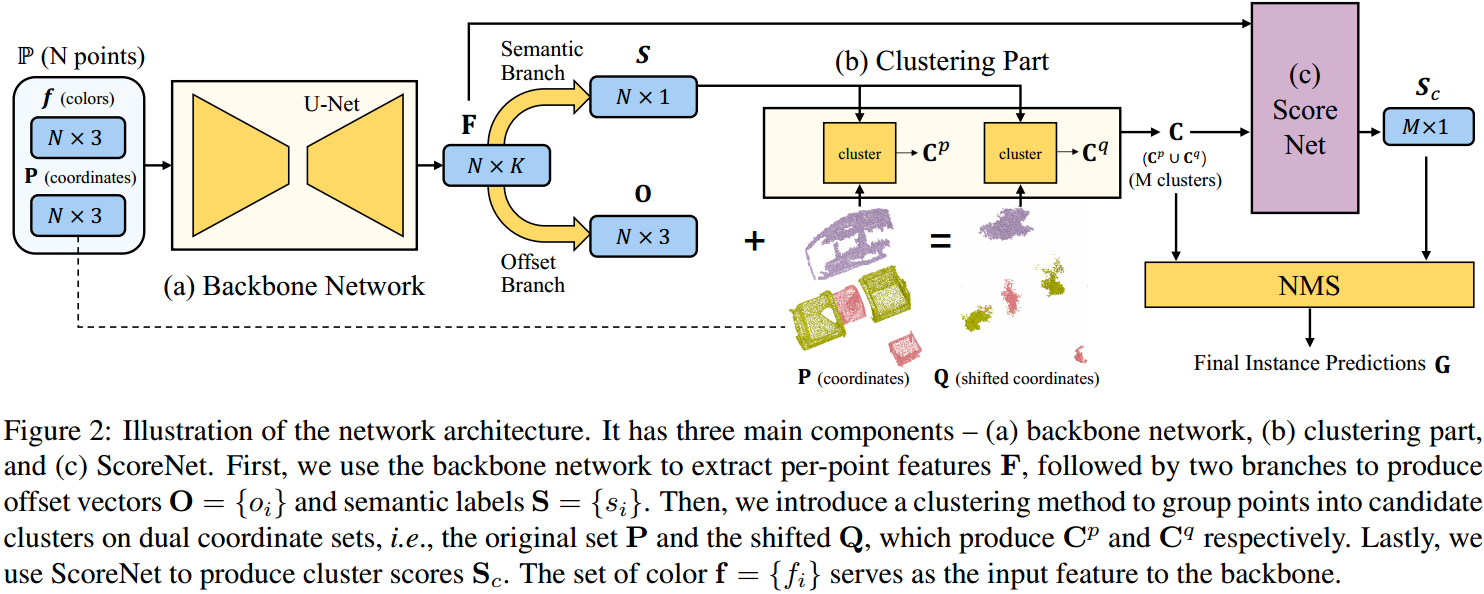如图 1. 所示，整个网络由三部分构成：Backbone，Clustering Part，ScoreNet。Backbone 我们已经很熟悉了，输入为点云以及点云的其它属性比如 rgb 信息，输出为每个点提取的局部-全局特征 \(\mathbf{F} = \{F _ i\}\in\mathbb{R} ^ {N\times K}\)，这里不作展开。然后用提取的特征 \(\mathbf{F}\) 通过两个分支分别作 Semantic Segmentation 以及预测每个点与该点对应的目标重心点的 Offset，得到每个点的类别 \(s _ i\) 以及 \(o _ i=(\Delta x _ i,\Delta y _ i,\Delta z _ i)\)。然后经过 Clustering Part 作 Instance 聚类。最后用 ScoreNet 预测 Instance 的分数，用于 NMS 去除重合的 Instance。
2. Backbone
对于 Semantic Segmentation Branch，在 \(\mathbf{F}\) 之后加入 MLP 网络输出语义类别分数 \(\mathbf{SC}=\{sc _ 1,...,sc _ N\}\in\mathbb{R}^{N\times N _ {class}}\)。最终的类别 \(s _ i = \mathrm{argmax}(sc _ i)\)。
对于 Offset Prediction Branch，输出 \(N\) 个点的 \(\mathbf{O}=\{o _ 1,...,o _ N\}\in\mathbb{R} ^ {N\times 3}\)。采用 L1 Loss： \[ L _ {o_reg} = \frac{1}{\sum _ i m _ i}\sum _ i\Vert o _ i-(\hat{c} _ i-p _ i)\Vert\cdot m _ i\tag{1}\] 其中 \(\mathbf{m} = \{m _ i,...,m _ N\}\) 是一个二进制 mask，\(m _ i=1\) 表示第 \(i\) 个点属于一个 Instance。\(\hat{c} _ i\) 为 Instance 的重心： \[\hat{c} _ i=\frac{1}{N _ {g(i)} ^ I}\sum _ {j\in I _ {g(i)}}p _ j\tag{2}\] 其中 \(N _ {g(i)} ^ I \) 表示 Instance \(I _ {g(i)}\) 中点的个数。此外，考虑到尺寸大的目标其边缘点的 offset 较难回归，所以加入方向约束的 loss： \[L _ {o _ dir}=-\frac{1}{\sum _ i m _ i}\sum _ i\frac{o _ i}{\Vert o _ i\Vert _ 2}\cdot\frac{\hat{c} _ i-p _ i}{\Vert \hat{c} _ i-p _ i\Vert _ 2}\cdot m _ i\tag{3}\]
3. Clustering Part
有了点云的语义标签以及每个点相对目标物体重心的 offset 后，接下来将点云聚类成对应的 Instance。设点云原始坐标为 \(\mathbf{P}=\{p _ i\}\)，经过 offset 变换后坐标为 \(\mathbf{Q}=\{q _ i = p _ i+o _ i\in\mathbb{R} ^ 3\}\)。根据 \(\mathbf{Q}\) 来作聚类，能更容易的区分相邻的同类别的物体；但是对于目标的边缘点，offset 容易预测错误，所以再加上根据 \(\mathbf{P}\) 来作聚类。最终获得的聚类 Instance 为 \(\mathbf{C}=\mathbf{C} ^ p\cup\mathbf{C} ^ q=\{C _ 1 ^ p,...,C _ {M _ p}^p\}\cup\{C _ 1 ^ q,...,C _ {M _ q} ^ q\}\)。 
如图 2. 所示，聚类算法就是一个基于点集的 BFS 搜索，这里需要设定 ball query 的半径 \(r\)。
4. ScoreNet
经过基于坐标 \(\mathbf{P},\mathbf{Q}\) 聚类后，总共得到 \(\mathbf{C} = \{C _ 1,...,C _ M\}\)。因为这里面会有重叠的 Instance，所以 ScoreNet 用来评价这些 Instance 的质量，然后作 NMS 操作，从而达到综合两者聚类优势的效果。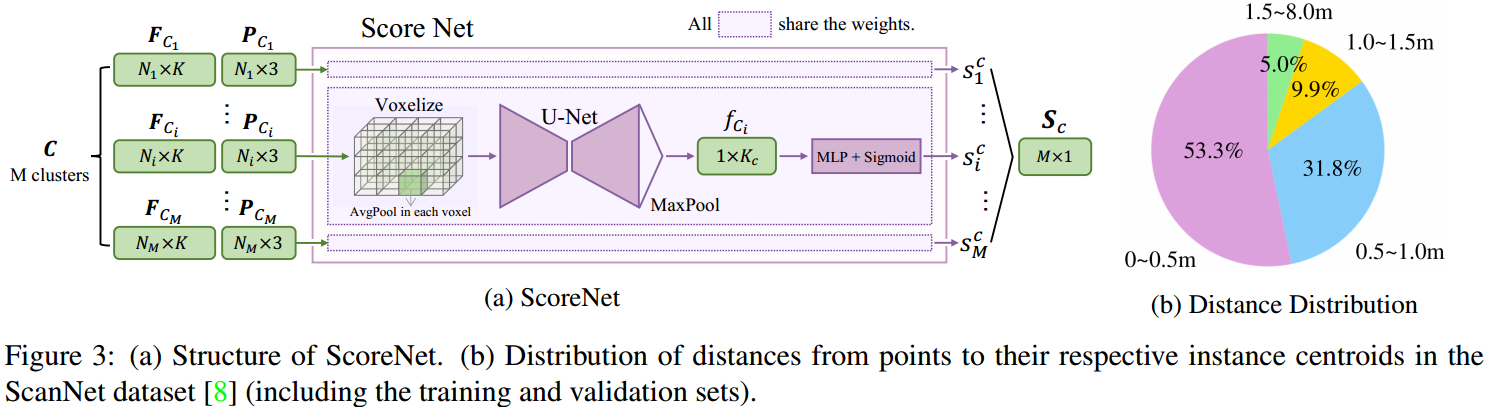 
如图 3. 所示，对于每个 Cluster，将其点特征加上点坐标作为点特征输入到网络。然后采用 Backbone 相似的结构，最终得到 Clustering 分数：\(\mathbf{S} _ c=\{s _ 1 ^ c,...,s _ M ^ c\}\)。
对于评价 cluster 质量的标签，可以直接用 0/1，但是本文使用了 soft 形式： \[\hat{s} _ i ^ c=\left\{\begin{array}{l}
0 &\;iou _ i < \theta _ l\\
1 &\;iou _ i < \theta _ h\\
\frac{1}{\theta _ h-\theta _ t}\cdot (iou _ i - \theta _ l) &\;otherwise
\end{array}\tag{4}\right.\] 其中 \(\theta _ l,\theta _ h \) 分别设为 0.25，0.75。然后用 binary cross-entropy 作为 Loss： \[L _ {c_score} = -\frac{1}{M}\sum _ {i=1} ^ M\left(\hat{s} _ i ^ clog(s _ i ^ c)+(1-\hat{s} _ i ^ c)log(1-s _ i ^ c)\right)\tag{5}\]
5. Experiments
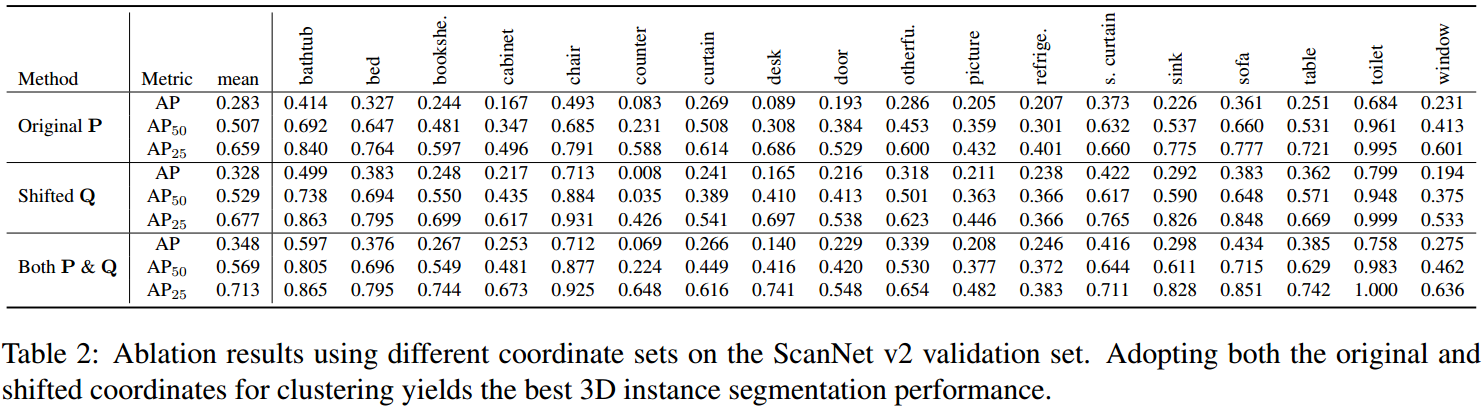如图 4. 所示，用 \(\mathbf{P,Q}\) 作聚类，效果提升还是比较明显的，能同时综合二者的聚类优势。
6. Reference
[1] Li.Jiang, PointGroup: Dual-Set Point Grouping for 3D Instance Segmentation
